1. Eksperymenty potwierdzające korpuskularną naturę światła i falową naturę cząstek.
Zjawisko fotoelektryczne polega na emisji elektronów z metalu pod wpływem promieniowania elektromagnetycznego.
Ilość wybijanych cząstek z katod elektronów zależy tylko od natężenia światła, a energia kinetyczna wybijanych elektronów zależy od częstości światła.
Podstawowe prawo rządzące efektem fotoelektrycznym zwane jest prawem Einsteina:
![]()
tzn. że energia padającego kwantu promieniowania zostaje zużyta na wykonanie pracy wyjścia elektronu i na nadanie elektronowi energii kinetycznej. Istnieje zatem częstość progowa υ0 zależna od rodzaju materiału fotokatody.
Pojedynczy elektron jest wybijany poprzez jeden foton, więc ilość wybijanych elektronów jest proporcjonalna do ilości padających fotonów, czyli do natężenia światła. Ze wzoru wynika też liniowa zależność między częstością światła padającego υ a energią kinetyczną elektronów, a niezależność między energią kinetyczną a natężeniem padającego promieniowania. Własności te świadczą o korpuskularnej naturze światła.
Zjawisko Comptona
Z doświadczenia wynika, że światło jest strumieniem fotonów, które natrafiając na swej drodze elektrony są odrzucane pod różnymi kątami w wyniku zderzeń. Fotony oddają część energii elektronom, więc następuje zmniejszenie częstości światła rozproszonego na elektronach a zwiększenie długości fali świetlnej. Przy zderzeniu sprężystym obowiązuje zasada zachowania energii i pędu:
![]()
![]()
Po uwzględnieniu wzorów teorii względności otrzymuje się wyrażenie na zmianę długości fali promienia rozproszonego:
![]()
gdzie Φ - kąt rozpraszania.
Efekt Comptona potwierdza kwantowy charakter promieniowania elektromagnetycznego oraz konieczność przypisania kwantom energii pewnej masy oraz pędu.
Dyfrakcja elektronów
Elektrony, mimo, że są cząstkami i dochodzą do detektora zawsze w jednakowych porcjach zachowują się jak fale.
Doświadczenie Davissona i Gremera
Podczas odbicia strumienia elektronów z działa elektronowego od kryształów (siatka dyfrakcyjna w postaci sieci atomowej kryształu) zaobserwowano efekty interferencyjne tzn. maksima i minima natężenia odbitych elektronów, które były w jednoznaczny sposób określone przez prędkość elektronów, orientację kryształu i kąt obserwacji. Doświadczenie potwierdziło hipotezę de Broigle'a o możliwości przypisania obiektom, o których zwykle myślimy jak o cząstkach, długości fali λ = h/p.
Z doświadczenia wynika wzór:
dsinθ = mλ
d - odległość między płaszczyznami atomowymi płytki
m - liczba naturalna
λ - maksima długości fal.
2. Model atomu Bohra - podstawowe założenia
Model atomu wodoru według Bohra to model planetarny. Wokół dodatnio naładowanego jądra atomu wodoru (proton), w którym skupiona jest praktycznie cała masa, krąży po kołowej orbicie lekki naładowany ujemnie elektron. Oddziaływanie między dodatnio naładowanym jądrem a ujemnym elektronem jest oddziaływaniem kulombowskim. Do tych prostych, klasycznych założeń Bohr dodał dwa postulaty:
a. Elektron nie może krążyć po dowolnej orbicie.
Dla danego elektronu dozwolone są tylko takie orbity, dla których iloczyn pędu elektronu i odległości elektronu od jądra (moment pędu) jest całkowitą wielokrotnością stałej Plancka podzielonej przez 2π:
![]()
Postulatowi temu towarzyszy odrzucenie zasad elektrodynamiki klasycznej dla zjawisk wewnątrz atomowych: elektron na orbicie stacjonarnej nie wypromieniowuje energii w postaci fal elektromagnetycznych o widmie ciągłym. Taki model atomu nie byłby bowiem trwały: energia kinetyczna elektronu malałaby, a razem z nią prędkość i promień orbity. Po pewnym czasie elektron w ruchu spiralnym spadłby na jądro, a emitowane fale elektromagnetyczne zmieniałyby się w sposób ciągły.
b. Każda emisja lub absorpcja energii przez atom odpowiada przejściu elektronu pomiędzy dwiema orbitami stacjonarnymi.
Promieniowanie emitowane podczas takiego przejścia jest jednorodne i jego częstość określana jest wzorem:
![]()
h - stała Plancka, E1 i E2 energie układu w obu stanach stacjonarnych. Prawa mechaniki opisują równowagę dynamiczną elektronów w stanach stacjonarnych, ale nie stosują się do przechodzenia elektronu pomiędzy dwoma stanami stacjonarnymi.
Siła dośrodkowa kulombowska:
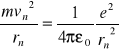
Stąd uwzględniając postulat a) otrzymuje się wzór na promień orbity stacjonarnej:
![]()
3. Równanie Schrödingera
Jest to różniczkowe równanie falowe opisujące nierelatywistyczny ruch cząstki w polu sił potencjalnych (fale materii). Dwie podstawowe własności równania S. to jego liniowość (tak, aby można je było superponować dla uzyskania efektów interferencyjnych w przypadku trójwymiarowym i konstrukcji paczek falowych) oraz współczynniki równania zawierające wyłącznie stałe (h, m, q), a nie parametry charakteryzujące ruch cząstki (pęd, energia, częstość). Dwie postaci równania S. dla przypadku jednowymiarowego:
![]()
- zależne od czasu
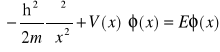
- stacjonarne
Lewa strona pierwszego równania to hamiltonian układu (uzupełniony o energię potencjalną oddziaływania V charakteryzującą oddziaływanie cząstek w mechanice klasycznej) pomnożony przez funkcję falową ψ. Prawa strona to pochodna funkcji falowej pomnożona przez mnożnik ih - równanie odzwierciedla fakt, że funkcja falowa opisuje własności układu w pewnej chwili czasu oraz we wszystkich późniejszych chwilach, a więc jej pochodna powinna się wyrażać samą funkcją falową.
Równanie drugie (stacjonarne) wyprowadzone zostało z pierwszego przy uwzględnieniu, że dla układu stacjonarnego możliwe jest rozdzielenie funkcji falowej na iloczyn funkcji położenia oraz funkcji czasu:
![]()
4. Interpretacja funkcji falowej w mechanice kwantowej
Funkcja falowa ψ(x, y, z, t) opisuje stan układu kwantowego. Ma trzy podstawowe własności:
może interferować sama ze sobą, tłumacząc tym samym wyniki doświadczeń dyfrakcyjnych (obrazujących zasadę nieoznaczoności i komplementarności w fizyce kwantowej)
przyjmuje duże wartości w otoczeniu punktu, gdzie istnieje duże prawdopodobieństwo znalezienia cząstki lub fotonu, a wszędzie indziej małe
opisuje zachowanie pojedynczej cząstki lub fotonu, a nie statystyczny rozkład dużej ilości takich cząstek.
Funkcja falowa ma charakter statystyczny, nie opisuje bezpośrednio żadnych mierzalnie istniejących zjawisk. Interpretację fizyczną ma wyłącznie moduł funkcji falowej, oznaczający gęstość prawdopodobieństwa znalezienia cząstki w danym miejscu.
Dla przypadku jednowymiarowego:
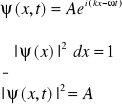
5. Zasada nieoznaczoności (nieokreśloności)
Wśród wielkości fizycznych opisujących zachowanie układu atomowego można wyróżnić pary o tej własności, że niemożliwe jest jednoznaczne przeprowadzenie pomiaru obu wielkości z danej pary (obie wielkości są względem siebie sprzężone w sensie hamiltonowskim). Iloczyn nieoznaczoności wartości obu zmiennych musi być co najmniej rzędu stałej Plancka h podzielonej przez 2π, czyli:
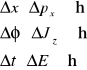
6. Cechy charakterystyczne poziomów w studni potencjału
W prostokątnej studni potencjału:
![]()
dla ![]()
![]()
dla ![]()
obiekt poruszający się w obszarze ![]()
może przyjmować tylko pewne dozwolone wartości energii opisane wyrażeniem:
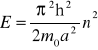
, ![]()
przy czym w studni skończonej (prostokątnej) ich liczba jest również skończona, a każdej wartości n odpowiada funkcja falowa o innym kształcie:
![]()
Te tzw. poziomy energetyczne występują w tym większych odstępach, im mniejsza szerokość studni. Przy jej zwężaniu następuje wypychanie poziomów energetycznych do góry - przy zbyt małej głębokości lub szerokości studni może nie pojawić się żaden dozwolony stan energetyczny. Dla dostatecznie szerokich studni odstępy między poziomami niemierzalnie małe, stąd ciągłość poziomów w skali makro.
7. Operatory w fizyce kwantowej
Operator - obiekt matematyczny, którym działając na funkcję uzyska się inną funkcję:
![]()
Postulat 2a mechaniki kwantowej stwierdza, że każdej obserwabli (wielkości fizycznej) odpowiada operator. Od operatorów stosowanych w formalizmie matematycznym mechaniki kwantowej wymaga się, aby były:
1) liniowe, tj.
![]()
2) samosprzężone (hermitowskie), tj. jeśli dla dowolnych funkcji fi, fj znikających w nieskończoności zachodzi warunek:
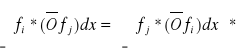
Własności operatora hermitowskiego:
wartości własne operatora są rzeczywiste (stąd stosowalność operatora w mechanice kwantowej)
funkcje własne operatora odpowiadające różnym wartościom własnym są ortogonalne
dowolna kombinacja liniowa zdegenerowanych funkcji własnych jest także funkcją własną z tą samą wartością własną; ze zbioru tych funkcji wybrać można 2 funkcje, które będą jednocześnie ortogonalne i unormowane, tj. orthonormalne, tj.
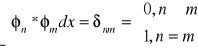
zbiór funkcji własnych operatora jest zbiorem zupełnym, tzn. dowolna funkcja falowa, która na brzegach obszaru ma takie same własności jak funkcje własne [spełniająca te same warunki brzegowe], może być przedstawiona w postaci liniowej kombinacji funkcji własnych:
![]()
Jest to uogólnienie rozwinięcia funkcji (niekoniecznie okresowej) w szereg Fouriera.
Wg postulatu 4 położenie i pęd w mechanice kwantowej są reprezentowane przez operatory:
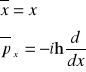
- dla przypadku jednowymiarowego
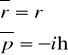
- dla przypadku trójwymiarowego.
8. Równanie Schrödingera jako równanie własne dla operatora
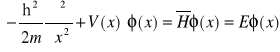
Jest to zagadnienie własne operatora hamiltonowskiego dla przypadku jednowymiarowego. Wynikające z niego dozwolone wartości energii są wartościami własnymi hamiltonianu, a funkcje falowe to funkcje własne hamiltonianu.
9. Komutator. Operatory komutujące
Komutator operatorów określony jest relacją:
![]()
Operatory komutują, jeżeli są przemienne:
![]()
![]()
Operatory zgodne
Dwie obserwable są zgodne, jeżeli ich operatory posiadają ten sam zbiór funkcji własnych (wartości własne są różne):
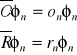
Operatory zgodne komutują. W konsekwencji dwie kompatybilne obserwable można mierzyć jednocześnie z dowolną dokładnością. Do obserwabli niekomutujących stosuje się relacja nieoznaczoności (nieokreśloności).
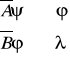
gdy komutują λ losowa, niezwiązana z φ
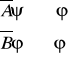
gdy nie komutują
10. Bariera potencjału (tunelowanie)
Załóżmy, że cząstka pada z lewej strony na prostokątną barierę potencjału o wysokości V0 i szerokości a. Zjawisko tunelowe polega na przenikaniu cząsteczki przez barierę potencjału (zjawisko to jest wykluczone w świecie makroskopowym).
Rozwiązując równanie Schrodingera dla trzech obszarów (przed, wewnątrz i za barierą) można wykazać, że funkcja falowa nie zanika w obszarze za barierą potencjału (indeks III). Oznacza to, że istnieje skończone prawdopodobieństwo przeniknięcia bariery. Warunkiem na przeniknięcie jest jeśli nieokreśloność położenia cząstki jest większa od szerokości a bariery:
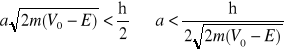
Równania S. dla trzech obszarów:
I. ![]()
![]()
II. ![]()
![]()
III. ![]()
![]()
W obszarze III brak jest energii potencjalnej dla fali `w prawo', od której fala mogłaby się odbić, zatem G = 0. Przy takim określeniu kierunku padania mamy:
![]()
- fala padająca (incident) ![]()
![]()
- fala odbita (reflected) ![]()
(energie)
![]()
- fala przechodząca (transmitted) ![]()
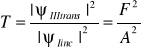
Prawdopodobieństwo przejścia i odbicia cząstki (elektronu) określają współczynniki:
odbicia
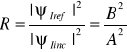
przejścia R+T = 1
11. Cechy charakterystyczne oscylatora kwantowego
Równanie S. dla oscylatora:
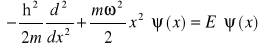
Wprowadzając zmienną: ![]()
oraz operatory kreacji i anihilacji otrzymujemy:
![]()
Uproszczone w ten sposób równanie S. daje rozwiązania w postaci wartości własnych - skwantowanych poziomów energetycznych:
![]()
Funkcji własnej ψ odpowiada jedna wartość własna energii, zatem poziomy energetyczne nie są zdegenerowane. Najniższy poziom energii dla n = 0 jest dodatni, czyli oscylator kwantowomechaniczny nigdy się nie zatrzyma, nie można zatem osiągnąć temperatury 0 K. Jest to w pełni zgodne z zasadą nieoznaczoności - gdyby bowiem oscylator zatrzymał się, miałby znany zerowy pęd oraz znane położenie.
Widmo oscylatora kwantowego jest dyskretne. Drgania cząsteczek tylko w przybliżeniu pasują do modelu oscylatora harmonicznego, zgodność występuje dla najniższych poziomów energii, czyli dla małych drgań cząsteczek. Dla dużych drgań cząsteczek, powyżej pewnej wartości x energia przyjmuje stałą wartość.
Stany (poziomy) energetyczne oscylatora kwantowego są równoodległe, rozkład energii jest nieciągły. Do ok. 100 K w ekwipartycji energii uczestniczą tylko translacyjne stopnie swobody cząstek, do ok. 1000 K - stopnie translacyjne oraz rotacyjne. Dla wysokich temperatur powyżej 1500 K w ekwipartycji energii uczestniczą również stopnie oscylacyjne. Wraz ze wzrostem temperatury zmienia się zatem ciepło właściwe materii.
12. Rotator kwantowy (hamiltonian i własności rozwiązań)
Hamiltonian rotatora kwantowego zapisuje się we współrzędnych sferycznych.
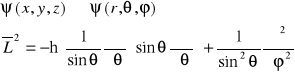
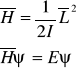
Energia rotatora nie zależy od liczby kwantowej m. Dla danej liczby J:
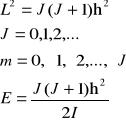
2J+1 funkcji stanu odpowiada tej samej energii - stany charakterystyczne energii (oraz kwadratu momentu pędu) są (2J+1)-krotnie zdegenerowane. Wartości własne rzutu momentu pędu na oś z są również kwantowane:
![]()
13. Hamiltonian i liczby kwantowe dla atomu wodoru
Hamiltonian opisujący ruch dwu cząstek (jądra i elektronu) przyciągających się wzajemnie z siłą zależną tylko od ich względnej odległości ma postać:
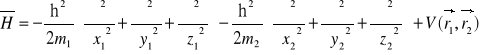
lub wprowadzając współrzędne środka masy X, Y, Z oraz współrzędne względne x, y, z:
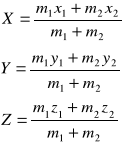
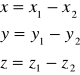
oraz masę zredukowaną i masę całkowitą układu:
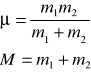
otrzymuje się alternatywną postać hamiltonianu:
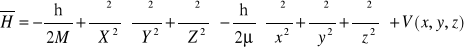
Ruch elektronu w atomie scharakteryzowany jest za pomocą: energii, momentu pędu, rzutu momentu pędu na wybraną oś, rzutu spinu elektronu. Każda z tych zmiennych dynamicznych jest wielkością kwantowaną; określają to liczby kwantowe:
n = 0,1,2,3,… - główna liczba kwantowa, określa wartość energii elektronu
n=nr+l+1
nr - radialna liczba kwantowa
l - poboczna (orbitalna) liczba kwantowa, określa wartość momentu pędu elektronu
l = 0,1,2,…, (n-1)
Oznaczenia orbitali stosowane w chemii kwantowej: 0 - s, 1 - p, 2 - d, 3 - f.
m - magnetyczna liczba kwantowa, określa wartość rzutu momentu pędu na oś z
![]()
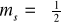
- magnetyczna liczba spinowa, określa rzut własnego momentu pędu na wybraną oś
Stan zdegenerowany elektronu występuje, gdy tę samą energię mogą mieć elektrony w różnych stanach kwantowych, określanych liczbami kwantowymi.
14. Zniesienie degeneracji ze względu na liczbę kwantową orbitalną i magnetyczną
Dla danego n mamy ![]()
funkcji własnych.
W atomie wieloelektronowym następuje zniesienie degeneracji ze względu na orbitalną liczbę kwantową l (czyli różne l - różne energie). Spowodowane jest to wzajemnym oddziaływaniem elektronów:
- przyciąganie elektrostatyczne każdego elektronu z jądrem
- odpychanie elektrostatyczne elektronów między sobą
- oddziaływania magnetyczne elektronów.
Elektron bliższy jądra jest pod działaniem potencjału ![]()
, gdzie Z - liczba elektronów, a elektron na dalszych orbitach czuje potencjał pomniejszony. W pobliżu jądra występuje mniej dokładne ekranowanie ładunku dodatniego przez pozostałe elektrony. Stąd energia elektronu zależy nie tylko od liczby n, ale również od l (elektrony o mniejszym momencie pędu docierają bliżej jądra).
15. Zachowanie się momentu magnetycznego w stałym polu magnetycznym
Traktując atom jako obwód elektryczny otrzymujemy zależności:
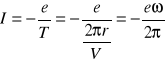
- natężenie prądu
![]()
- dipolowy moment magnetyczny [Am2]
![]()
, ![]()
- moment pędu elektronu
![]()
- magneton Bohra (moment magnetyczny na 1. orbicie w atomie wodoru)
![]()
- moment magnetyczny elektronu o liczbie kwantowej l
Dla momentu magnetycznego w polu magnetycznym:
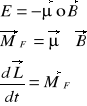
Mamy zmianę momentu pędu pod wpływem działającego momentu siły. Wektor momentu pędu (a zatem również proporcjonalnego do niego momentu magnetycznego) wykonuje ruch precesyjny wokół wektora pola B. Częstość precesji jest proporcjonalna do wartości pola magnetycznego:
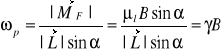
gdzie:
γ - stosunek giromagnetyczny.
16. Spin i moment magnetyczny elektronu - dozwolone wartości
Elektron ma własny moment pędu zwany spinem i związany z nim własny moment magnetyczny μs - magnetyczny moment spinowy. Wprowadzenie tych wielkości wiąże się z faktem, że orbitalny moment pędu ![]()
wyraża się przez współrzędne i pędy, wielkość L2 nie jest na ogół stałą ruchu. Orbitalna liczba kwantowa nie musi być dobrze określona i może służyć do opisu cząstki jedynie w pewnych przypadkach.
Wprowadzając spinowy moment pędu S, który spełnia podstawowe związki komutacyjne, S2 komutuje ze zmiennymi dynamicznymi i S nie da się wyrazić przez r i p, otrzymujemy operator S2 będący stałą ruchu o dozwolonych wartościach:
![]()
gdzie:
s - spinowa liczba kwantowa, całkowita (dla np. fotonów) lub połówkowa (dla np. elektronów).
Dodatkowo rzut spinu na oś z wyraża się zależnością:
![]()
Spinowy moment magnetyczny:
![]()
17. Oddziaływanie spin-orbita
Każdy elektron w atomie ma dwa momenty pędu: orbitalny i spinowy. Momenty te oddziałują ze sobą, a także oddziałują ze sobą momenty magnetyczne różnych elektronów. Sposób powiązania tych momentów nazywany jest sprzężeniem spin-orbita. Typy sprzężeń:
- sprzężenie Russela-Saundersa (L-S): występuje w atomach, gdzie oddziaływania spin-orbita jest małe w porównaniu do oddziaływań elektrostatycznych; polega na dodaniu wektorowym momentów spinowych wszystkich elektronów - powstaje wypadkowy moment spinowy atomu:
![]()
Podobnemu sumowaniu podlegają magnetyczne momenty orbitalne tworząc wypadkowy moment orbitalny:
![]()
- sprzężenie J-J: zwykle w atomach prostych, w których oddziaływanie spin-orbita jest duże; sumuje się momenty spinowe i orbitalne dla każdego elektronu, tworząc wypadkowy moment magnetyczny elektronu
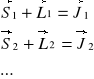
Następnie dodaje się momenty poszczególnych elektronów:
![]()
18. Rozszczepienie poziomów w polu magnetycznym. Efekt Zeemana
Zewnętrzne słabe pole magnetyczne rozszczepia poziomy energetyczne w atomie zdejmując degenerację ze względu na kierunki pełnego momentu pędu.
Pole magnetyczne B0 powoduje precesję spinowego momentu magnetycznego (analogicznie jak w przypadku momentu magnetycznego orbitalnego) po powierzchniach stożkowych stycznych w punkcie. Rozszczepienie pociąga za sobą rozbicie poziomu energetycznego z różnicą energii (tzw. energią rozszczepienia) wynoszącą:
![]()
19. Zjawisko rezonansu magnetycznego (jądrowego i elektronowego)
Elektronowy rezonans magnetyczny zachodzi, gdy elektron poddany jest działaniu zewnętrznych pól magnetycznych o kierunkach wzajemnie do siebie prostopadłych:
![]()
przy czym wektor indukcji jednego z pól jest zmienny w czasie:
![]()
Działanie pola okresowo zmiennego powoduje regularne, harmoniczne przerzucanie elektronu między rozszczepionymi pod wpływem pola B0 dyskretnymi poziomami energetycznymi (w sensie mechanicznym: nutacje ruchu precesyjnego wektora momentu magnetycznego μs względem wektora B0).
Jeżeli ![]()
(częstość precesji), to nutacje mają maksymalną amplitudę, moment magnetyczny ulegać będzie przekręcaniu (spin zmienia orientację z położenia +½ w -½). W sensie kwantowomechanicznym są to fale elektromagnetyczne o częstościach gigahercowych, tzw. elektronowy rezonans paramagnetyczny (ESR, EPR).
![]()
,
υ - rzędu GHz.
EPR nie ma zastosowania w strukturach nieuporządkowanych (złożonych z atomów różnych pierwiastków), ponieważ nie występuje w nich znane jednorodne pole magnetyczne - brak jednolitego tła do badania składu materii. W strukturach takich wykorzystuje się rezonans jądrowy NMR, zachodzący dla jąder atomowych. Moment magnetyczny jądrowy nie zależy bowiem od otoczenia - jądro jest dobrze izolowane przez chmurę elektronową. Fale rezonansowe mają w tym przypadku częstotliwości megahercowe, wygodne do badania w zakresie fal radiowych.
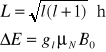
μN - magneton jądrowy
20. Atom w stałym polu elektrycznym. Efekt Starka
Zmiana poziomów energii atomu spowodowana wpływem jednorodnego zewnętrznego pola elektrycznego o natężeniu E (zmiana częstości widm optycznych) nosi nazwę zjawiska Starka. Stanom o różnych wartościach rzutu całkowitego momentu pędu na kierunek pola Jz odpowiadają różne energie, tj. pole elektryczne znosi degenerację względem kierunków momentu pędu.
Atomy w substancjach obojętnych tworzą dipole elektryczne (samoistne lub indukowane). Moment dipolowy jest proporcjonalny do natężenia pola elektrycznego:
![]()
Stałe, jednorodne pole elektryczne ustawia moment dipolowy równolegle do linii pola:
![]()
Dla pola gradientowego ![]()
występuje wciąganie momentów dipolowych do środka pola.
Zjawisko Starka liniowe - rozszczepienie poziomów na podpoziomy jest symetryczne, a wielkość przesunięcia podpoziomów względem poziomu nierozszczepionego jest proporcjonalna do natężenia pola elektrycznego:
![]()
Zjawisko Starka kwadratowe - środek ciężkości podpoziomów jest przesunięty w stronę mniejszych energii w stosunku do poziomu nierozszczepionego, a przesunięcie podpoziomów jest proporcjonalne do kwadratu natężenia pola:
![]()
Poziom energetyczny może pozostać nierozszczepiony (dla J = ½) - następuje tylko jego podwyższenie, o czym mówi twierdzenie Kramersa.
21. Przejścia wywołane zmiennym polem elektrycznym. Reguły wyboru
Zmienne pole elektryczne określone jest wektorem natężenia pola:
![]()
Zakładając polaryzację pola wzdłuż osi z:
![]()
otrzymuje się związki:
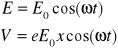
gdzie V jest energią oddziaływania fali. Wprowadzając oznaczenia poziomów energetycznych atomu:
E0 - poziom podstawowy ψ(1)
E1 - poziom wzbudzony ψ(2)
oraz zakładając, że:
![]()
otrzymuje się rozwiązanie równania S. w postaci:
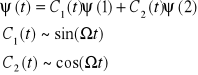
odzwierciedlające oscylacyjne przechodzenie atomu z jednego stanu energetycznego w drugi. Reguły wyboru pozwalają określić, które z przejść pomiędzy poziomami energetycznymi w atomie są wysoce prawdopodobne, mało oraz wcale nieprawdopodobne. Absorpcja następuje przy przejściu atomu ze stanu podstawowego na wzbudzony przy jednoczesnym pochłonięciu kwantu ![]()
. Emisja polega na wyprowadzaniu kwantu ![]()
podczas przejścia atomu ze stanu wzbudzonego w podstawowy. Jeżeli elektron przechodzi do stanu niższego z jednoczesną emisją światła, to emisja nazywana jest spontaniczną.
22. Konsekwencje nierozróżnialności cząstek dla wiązania chemicznego
W opisie kwantowym cząstki są nierozróżnialne, gdy są to cząstki tego samego rodzaju (identyczne). Zasada nieoznaczoności oznacza bowiem niemożliwość obserwacji toru cząstki, czyli zlokalizowanie i ponumerowanie w pewnej chwili czasu wszystkich cząstek nie daje nic z punktu widzenia ich identyfikacji w chwilach późniejszych.
Równanie S. dla większej liczby cząstek jest rozwiązywalne tylko przy założeniu, że cząstki nie oddziałują na siebie. W wyniku przestawienia cząstek miejscami funkcja falowa układu może zmieniać się tylko o nieistotny czynnik fazowy. Przy dwóch przestawieniach powinno zatem być:
![]()
czyli:
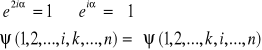
Taki wynik ma sens fizyczny, ponieważ tylko kwadrat funkcji falowej ma interpretację fizyczną. Istnieją zatem 2 rozwiązania: funkcja falowa może być symetryczna (nie zmienia znaku przy zamianie cząstek) lub antysymetryczna (zamiana cząstek zmienia znak funkcji).
Elektrony w atomie opisywane są funkcją falową antysymetryczną - są to fermiony. Ich cechą charakterystyczną jest fakt, że dwa fermiony nie mogą być w tym samym stanie kwantowym, zatem przeskok elektronu z jednego poziomu energetycznego na drugi pociąga przeskok odwrotny drugiego elektronu tak, aby sumaryczna energia układu pozostała stała. Jest to podstawa budowy cząsteczkowych wiązań chemicznych. W cząsteczce nie można już powiedzieć, że elektron jest związany z danym jądrem atomowym, stan układu różni się od stanu atomów nie oddziałujących.
23. Podstawowe założenia metody kombinacji liniowych i metody wiązań walencyjnych
a) Metoda wiązań walencyjnych
Omówienie na przykładzie cząsteczki H2:
A i B - jądra atomowe
1 i 2 - elektrony
Gdy odległość między jądrami atomów rAB duża, możemy traktować cząsteczkę jako dwa nie oddziałujące atomy. Przy takim założeniu słuszne są poniższe wyrażenia dotyczące hamiltonianu, energii oraz funkcji falowej:
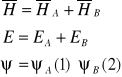
ponieważ:
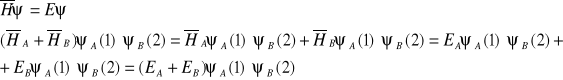
Przy zbliżaniu jąder atomów do siebie prawdopodobieństwo znalezienia elektronu 1 występuje zarówno przy jądrze A, jak i przy jądrze B (cząstki 1 i 2 są identyczne). Funkcja falowa ma wówczas postaci:
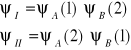
Sumaryczna funkcja falowa jest kombinacją liniową tych funkcji:
![]()
Ostatecznie równanie S. ma postać:
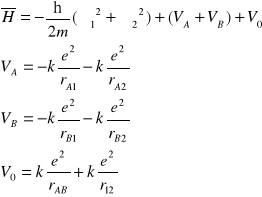
i jest rozwiązywalne tylko za pomocą metod przybliżonych.
b) Metoda kombinacji liniowych - służy do obliczania energii stanu podstawowego cząsteczki i jest uogólnieniem metody wiązań walencyjnych na większą liczbę cząstek:
![]()
![]()
- dowolne funkcje
Z równania S.:
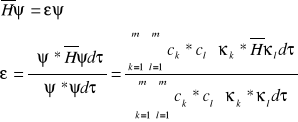
Wprowadzając oznaczenia:
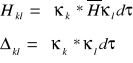
i różniczkując równanie![]()
dla energii stanu podstawowego otrzymujemy układ równań liniowych:
![]()
n = 1,2,…,m
którego kwadratowy wyznacznik przyrównujemy do 0 dla wyznaczenia rozwiązania nietrywialnego. Najniższa otrzymana wartość ε jest najlepszym przybliżeniem energii stanu podstawowego układu (cząsteczki).
24. Uwzględnienie jonowości wiązania
Metoda wiązań walencyjnych dość dobrze opisuje wiązania kowalentne. Dla wiązań jonowych należy dodatkowo uwzględnić funkcje falowe opisujące przeniesienie ładunku z jednego atomu do drugiego:
![]()
- gdy oba elektrony krążą wokół jądra A
![]()
- gdy oba elektrony krążą wokół jądra B.
Dla cząsteczek homojądrowych chemiczny sens struktur jądrowych jest niewielki. Dla cząsteczek heterojądrowych powinowactwo elektronu (energia wyemitowana przy tworzeniu się wiązania jonowego) dla różnych atomów jest różne. W tym przypadku funkcje ψIII i ψIV nie są równoznaczne i w wypadkowej funkcji wariacyjnej ψ należy je uwzględnić z różnymi stałymi.
25. Hybrydyzacja sp3, sp2, sp
Wiązania chemiczne nie muszą pochodzić od czystych orbitali s, p, d, f - mogą się pojawić tzw. orbitale zhybrydyzowane. Hybrydyzacja bierze się z faktu bardzo niewielkiej energii potrzebnej do przejścia z jednego orbitalu na drugi, orientacja przestrzenna orbitali zhybrydyzowanych pozwala zminimalizować elektryczne odpychania elektronów. Orbitale s i p mieszają się (wskutek oddziaływania) i tworzą wspólnie nowe stany - hybrydyzowane, równoległe orbitale. W atomie węgla C: (1s)2(2s)2(2px)1(2py)1:
Jeden elektron przechodzi z orbitalu s na p umożliwiając następujące hybrydyzacje:
sp - hybrydyzacja diagonalna (2 orbitale pod kątem 180° hybrydyzowane z orbitali s, p oraz 2 orbitale niezhybrydyzowane py i pz)
sp2 - hybrydyzacja trygonalna (3 orbitale pod kątem 120° hybrydyzowane z orbitali s, px, py - czwarty orbital niezhybrydyzowany pz)
sp3 - hybrydyzacja tetraedryczna (4 orbitale pod kątem 109° 28' utworzone przez 2 niesparowane elektrony z orbitalu s i 2 niesparowane elektrony z orbitali p).
Orbitale zhybrydyzowane mają inny kształt niż orbitale typu s lub typu p. Orbital hybrydyzowany skoncentrowany jest głównie po jednej stronie jądra atomowego i dzięki temu ma on silniejsze własności kierunkowe niż orbitale s i p. Hybrydyzacja orbitali występuje wyłącznie w cząsteczkach, nie w izolowanych atomach.
26. Wiązanie π i σ
Wszystkie wiązania pojedyncze są skierowane wzdłuż prostej łączącej jądra dwóch atomów i noszą nazwę wiązań σ. Przestrzeń wspólna wiązania jest symetryczna w stosunku do osi łączącej oba jądra atomów w cząsteczce. Pojedyncze wiązania mogą się tworzyć przez nałożenie się chmur elektronowych dwóch orbitali typu s, po jednym elektronie z każdego atomu, dając wiązanie typu s - s, jak to ma miejsce w cząsteczce H2. Atomy, które mają tylko niesparowane (wolne) elektrony typu p, tworzą wiązania typu p - p. Tego typu wiązanie występuje w cząsteczkach F2, Cl2, Br2 itp. Trzecim typem jest wiązanie s - p, pospolite m. in. w węglowodorach.
W węglowodorach nienasyconych, jak np. w etylenie, każdy z atomów węgla ma niesparowane elektrony na orbitalu p. Orbital ten nie jest hybrydyzowany i jest skierowany prostopadle do płaszczyzny wiązań σ, tzn. płaszczyzny cząsteczki. Równoległe do siebie chmury elektronowe obu orbitali p wskutek częściowego pokrycia się tworzą między obu atomami węgla dodatkowe wiązanie, zwane π. Ponieważ wiązania π powstają z niezhybrydyzowanych orbitali p lub d, nie wpływają one na kształt cząsteczki, zależy on bowiem od ukierunkowania w przestrzeni wiązań σ. Wiązanie π jest tym samym dużo słabsze od wiązania σ. Przestrzeń wzajemnego nakładania się orbitali jest prostopadła do osi łączącej jądra atomów w cząsteczce.
27. Natura widm cząsteczkowych
Emisja i absorpcja kwantów energii występuje w zakresie:
- widzialnym i nadfiolecie
- bliskiej podczerwieni
- dalekiej podczerwieni.
Mamy:
![]()
gdzie:
![]()
- energia przejścia elektronowego (rzędu 5÷10 eV)
![]()
- energia ruchów oscylacyjnych (dla cząsteczek dwuatomowych ![]()
eV)
![]()
- energia ruchów rotacyjnych (dla cząsteczek chemicznych rzędu 0,005 eV)
Długości fali dla poszczególnych energii wynoszą ![]()
:
λe < 1 μm - zakres widzialny, nadfiolet
λv = 12,5 μm - krótkofalowa podczerwień bliska
λr = 200 μm - długofalowa podczerwień daleka.
Przejścia elektronowe mogą pociągać za sobą szereg przejść oscylacyjnych. Stąd zamiast jednego prążka (np. fali o długości ok. 250 nm) otrzymuje się szereg prążków z odstępami co ok. 5 nm.
Każdemu przejściu oscylacyjnemu towarzyszą z reguły różne przejścia rotacyjne, stąd zamiast jednego prążka odpowiadającemu przejściu oscylacyjnemu otrzymamy szereg prążków w odstępach ok. 0,25 nm.
28. Funkcja falowa symetryczna i asymetryczna
Równanie S. dla większej liczby cząstek jest rozwiązywalne tylko przy założeniu, że cząstki nie oddziałują na siebie. W wyniku przestawienia identycznych cząstek miejscami funkcja falowa układu może zmieniać się tylko o nieistotny czynnik fazowy (stan układu nie powinien się bowiem zmienić). Przy dwóch przestawieniach powinno zatem być:
![]()
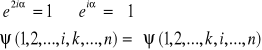
Taki wynik ma sens fizyczny, ponieważ tylko kwadrat funkcji falowej ma interpretację fizyczną. Istnieją zatem 2 rozwiązania: funkcja falowa może być symetryczna (nie zmienia znaku przy zamianie cząstek) lub antysymetryczna (zamiana cząstek zmienia znak funkcji).
Symetria funkcji falowej nie zależy od czasu. Jeśli ψ symetryczne, to:
![]()
symetryczne
![]()
symetryczne.
29. Fermiony
Fermiony są to cząstki opisywane przez funkcję falową antysymetryczną. Zasada budowy takiej funkcji dla dwóch identycznych cząstek 1,2 w dwóch różnych stanach kwantowych α, β:
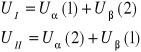
Rzeczywistość fizyczna opisywana jest przez sumy powyższych funkcji falowych. Dla dwóch fermionów w różnych stanach:
![]()
przy czym gdy α = β mamy zerowanie się funkcji falowej: Ua = 0, co nie ma sensu fizycznego. Fermiony nie mogą zatem znajdować się w tym samym stanie kwantowym (stąd różne spiny elektronów na tych samych orbitalach). Maksymalna liczba fermionów na zdegenerowanym poziomie energetycznym równa jest krotności degeneracji.
Fermiony posiadają ułamkową liczbę spinową - są to np. elektrony, protony i neutrony. Statystykę kwantową fermionów w układzie odizolowanym (o stałej energii wewnętrznej) opisuje rozkład Fermiego-Diraca.
![]()
- prawdopodobieństwo zapełnienia stanu kwantowego o energii E
![]()
- potencjał chemiczny w zerze absolutnym, zwany energią Fermiego (najwyższa energia stanu zapełnionego w T = 0 K)
Dla dużych energii E - EF >> 2kT rozkład Fermiego przechodzi w rozkład Boltzmana:
![]()
więc dla dużych energii cząstek lub dużych temperatur znika znaczenie kwantowych własności cząstek i mogą one być opisywane jako cząstki klasyczne.
30. Bozony
Bozony są to cząstki opisywane symetryczną funkcją falową. Dla układu n takich cząstek funkcja taka ma postać sumy permutacji iloczynów pojedynczych funkcji falowych:
![]()
gdzie:
![]()
- operator permutacji cząstek.
Bozony są cząstkami o spinie całkowitym - np. fotony.
Statystykę kwantową bozonów opisuje rozkład Bosego-Einsteina:
![]()
Rozkład ten dla dużych energii również przechodzi w rozkład Boltzmana. Odchylenie w zachowaniu gazów cząstek Bosego i Fermiego od zachowania się gazu klasycznego nosi nazwę zwyrodnienia.
![]()
Tθ - temperatura degeneracji
k - stała Boltzmana
n - koncentracja cząstek
Gdy układ ma temperaturę T<Tθ, to jest układem zdegenerowanym, tzn. że własności kwantowe cząstek mają znaczenie (stosuje się statystyki F-D lub B-E). W przeciwnym razie układ jest niezdegenerowany i stosowalny jest rozkład Boltzmana.
Poniżej Tθ bozony przyjmują poziom energetyczny ε = 0. Wraz ze zbliżaniem się do T = 0 K następuje kondensacja wszystkich cząstek na najniższym poziomie energetycznym (tzw. kondensaty Bosego-Einsteina silnie oddziałujące z falą elektromagnetyczną - spowalniające światło).
Wyszukiwarka
Podobne podstrony:
I, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa, ściągi
poruszane zagadnienia na wykładzie, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchnio
Pytania Obrobka cieplna i powierzchniowa calosc, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i
jakaś teoria, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa, ściągi
sciaga abcd, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa, ściągi
ocip sciaga2, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa, ściągi
kolos 2-ocip, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa, ściągi
OCiP KOLOS!!!, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa, ściągi
I, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa, ściągi
Obróbka powierzchniowa i cieplna ściąga, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierz
skrót wykładu, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa, wykłady
Fazy rozwoju materiałów - ściaga, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa
Pomiary twardości, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa, wykłady
Obróbka powierzchniowa i cieplna - ściąga 01, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i po
Krystaliczna struktura metali - laborka, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powier
Wyzarzanie i hartowanie 01.txt, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa,
Wyzarzanie i hartowanie 03, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa, wykł
Odpuszczanie, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa, wykłady
Otrzymywanie Stali, Automatyka i Robotyka, Semestr 3, Obróbka cieplna i powierzchniowa, wykłady
więcej podobnych podstron