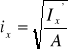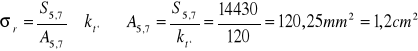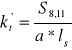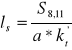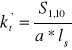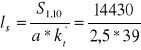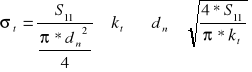Dane	Szkice i obliczenia	Wyniki
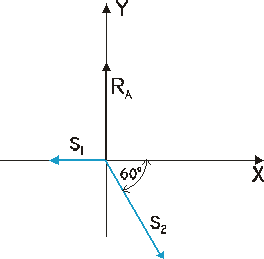
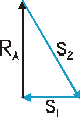
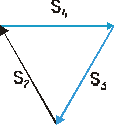
P = 25 kN RA = 25kN	Temat P = 25 kN a = 1500mm Obliczenie reakcji podpór Σ MiA = - P•a - P•2a + RB•3a = 0 RB = P = 25 kN Σ Fiy = RA + RB - P - P = 0 RA = P = 25kN Analiza kratownicy metodą analityczną Na niebiesko zaznaczono wektory o nieznanych wartościach Węzeł I Σ Fiy = RA - S1•sin60˚ = 0 → S2 = 28,86 kN Σ Fix = S2•cos60˚ - S1 = 0 → S1 = 14,43 kN	RA = 25 kN RB = 25 kN S1 = 14,43 kN S2 = 28,86 kN
Dane	Szkice i obliczenia	Wyniki
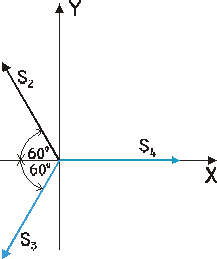
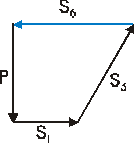
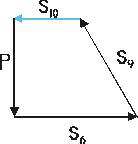
S2 = 28,86 kN S1 = 14,43 kN S3 = 28,86 kN	Węzeł III Σ Fiy = S2•sin60˚ - S3•sin60˚ = 0 → S3 = 28,86 kN Σ Fix = -S2•cos60˚ - S3•cos60˚ + S4 = 0 → S4 = 28,86 kN Węzeł II Σ Fiy = -P + S5•sin60˚ + S3•sin60˚ = 0 → S5 = 0 Σ Fix = S3•cos60˚ + S1 - S6 = 0 → S6 = 28.86 kN	S3 = 28,86 kN S4 = 28,86 kN S5 = 0 S6 = 28,86 kN

Dane	Szkice i obliczenia	Wyniki
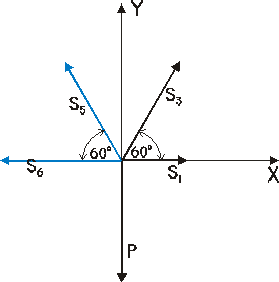
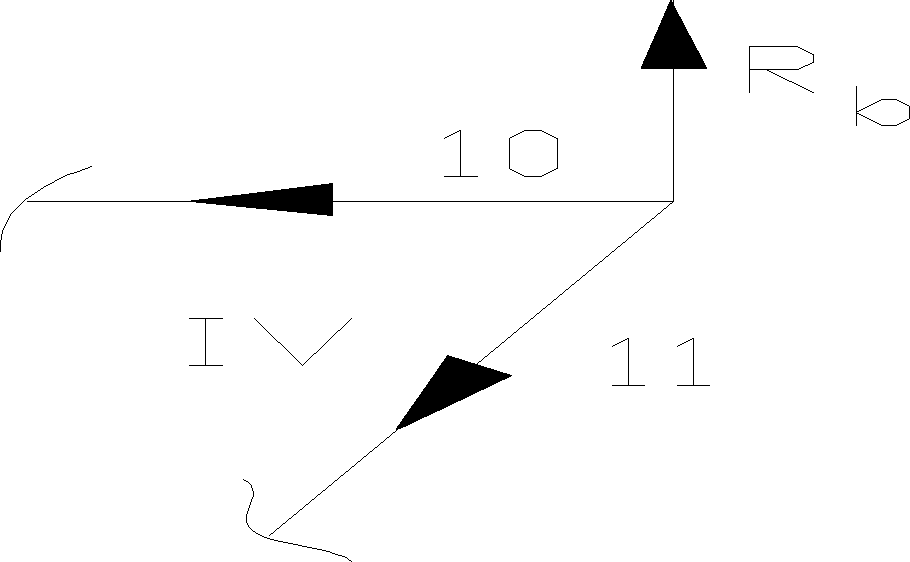
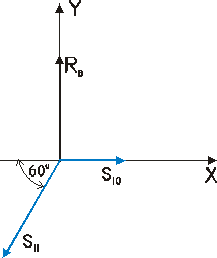
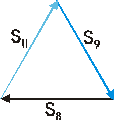
S4 = 28,86 kN S8 = 28,86 kN	Węzeł IV Σ Fiy = S7•cos60˚ = 0 → S7 = 0 Σ Fix = -S4 + S8 = 0 → S8 = 28,86 kN Węzeł VI Σ Fix = -S9•cos60˚ + S11•cos60˚ - S8 = 0 → S11 = 28,86 kN Σ Fiy = S9•sin60˚ + S11•sin60˚ = 0 → S9 = 28,86 kN	S7 = 0 S8 = 28,86 kN S11 = 28,86 kN S9 = 28,86 kN

Dane	Szkice i obliczenia	Wyniki
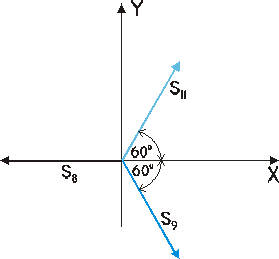
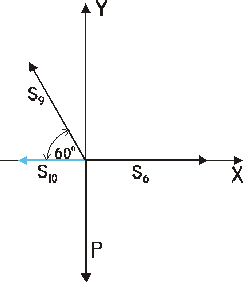
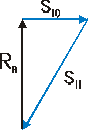
S11 = 28,86 kN S6 = 28,86 kN S10 = 14,43 kN S11 = 28,86 kN	Węzeł V Σ Fix = -S11 + S6 - S9•cos60˚ = 0 → S10 = 14,43 kN Węzeł VII Σ Fix = S10 - S11•cos60˚ = 0	S10 = 14,43 kN

Dane	Szkice i obliczenia	Wyniki
	Plan sił Cremony (jako sprawdzenie). Węzeł I Węzeł II Węzeł III Węzeł IV Węzeł V Węzeł VI

Dane	Szkice i obliczenia	Wyniki
	Węzeł VII Podsumowanie Siły w prętach mają następujące wartości: S1 = -14,43 kN S2 = 28,86 kN S3 = -28,86 kN S4 = -28,86 kN S5 = 0 S6 = -28,86 kN S7 = 0 S8 = 28,86 kN S9 = -28,86 kN S10 = -14,43 kN S11 = 28,86 kN. Minus oznacza, że pręt jest ściskany. Analiza węzła nr IV. Pręty 8 i 11 są rozciągane więc dobiorę ich profil korzystając z warunku na rozciąganie. Natomiast pręt 9 jest ściskany więc będę korzystał z warunku na wyboczenie.

Dane	Szkice i obliczenia	Wyniki
Re = 240 MPa xe = 2 S2 = 28,86 kN S11 = 28,86 kN S11 = -28,86 kN kc = 72 MPa Ix,y = 1,8 cm^4 A = 2,27 cm^2 g = 4 mm e= 8,7mm l=1500mm	Dobór materiałów, naprężeń dopuszczalnych i współczynników bezpieczeństwa. Wszystkie elementy kratownicy zostaną wykonane ze stali St3S. Dopuszczalne naprężenia na rozciąganie wynoszą. kr = Re/xe = 120 MPa. kc = 0,6*kr = 72 MPa. Dobór kształtowników na pręty nr 2 i 11. Σ2,11 = S2,11/A2,11 ≤ kc → A = S2,11/ kc A2,11 = 14430/72=200,4[mm^2]=2cm^2 Takie pole przekroju poprzecznego posiada kątownik L 30x30x4 Dobór kształtownika na pręt nr 11. Pręt ten ponieważ jest ściskany należy dobierać ze względu na wyboczenie (kątownik spawany obustronnie) Wstępny dobór kształtownika z warunku na ściskanie. Przyjmuje naprężenia ściskające kc=0,6*kr σc= ≤ kc*β → β*A9≥ Dobieram kątownik L30x30x4, rmax=5mm, r1max=2,5mm Sprawdzenie kątownika L30x30x4 z warunku na wyboczenie. Dla wybranego kształtownika odczytuje z norm moment bezwładności I oraz pole przekroju A. Obliczam moment bezwładności dla połączonego kątownika i blachy węzłowej, przyjmując jej grubość : gb=1,5*g Ix^'= Ix Iy^'= 2*(Iy+A*(e+gb/2)^2) Ponieważ Ix'< Iy' - zatem pręt jest bardziej narażony na wyboczenie względem osi x. Obliczam promień bezwładności: Korzystając ze wzoru λ = α•l/i obliczam smukłość pręta. λ = 119,2 Dla λ = 119,2 odczytuje z tablic wartość współczynnika β, który jest współczynnikiem zmniejszającym: β = 0,426 A = AL.* β A = 4,8 * 0,426 = 2,04 cm^4 Zatem warunek wyboczeniowy jest spełniony.	kc=72MPa kr = 120 MPa A2,11=2,27cm^2 β*A11= 2 cm^2 gb= 6,4 mm Ix' = 1,8 cm^4 Iy' = 8,7cm^4 ix = 0,89 cm L30x3045
Dane	Szkice i obliczenia	Wyniki
gmax = 4 mm z = 1 z0 = 0,65 kc = 72 MPa g1 = 3 mm g2 = 4 mm S2,11 = 28,86 kN k't = 46,8 MPa b = 30 mm e = 8,7 mm	Dobór blachy węzłowej. Korzystam z warunku: gbw = 1,6*gmax gdzie: gbw - grubość blachy węzłowej gmax - grubość najgrubszego elementu łączonego. gbw = 6,4 mm Ostatecznie dobieram blachę o grubości 8 mm. Blacha węzłowa jest wykonana z tego samego materiału co profile czyli St3S. 11. Dobór kształtowników na pręty 1 i 10. Takie pole przekroju poprzecznego posiada kątownik 25x25x3 o powierzchni A1,10=1,42 cm^2, Ix=Iy=0,80cm^4, e=0,71cm, a=25mm, g=3mm, rmax=3mm, r1max=3,5mm 12.Projektowanie połączenia spawanego dla katownika 11 Naprężenia dopuszczalne obliczą ze wzoru kt' = z•z0•kc gdzie: z - współczynnik jakości spoiny z0 - współczynnik uwzględniający charakter obciążenia statycznego kc - naprężenia dopuszczalne dla materiałów łączonych kt' = z*z0*kc [MPa] 13.Określenie grubości spoiny Wymiar „a” wszystkich spoin łączących kątowniki L25x25x3 oraz L30x30x4 z blachą węzłową przymuje jako: a = 0,7*g a1 = 2,1mm a2 = 2,8 mm Ze względów technologicznych przyjmuje wysokość spoiny równą a = 2,5 mm 14.Określenie długości spoiny w prętach nr 2 i 11. Obliczam sumaryczną obliczeniową długość spoin, tzn. ls = l1 + l2 ; przypadającą na jeden kątownik. → Spoiny ułożone na krawędziach półki kątownika znajdują się w różnych odległościach od osi działania siły S. Dla zapewnienia równomiernego obciążenia obydwu spoin należy spełnić warunek:	gbw = 8 mm kt' = 46,8 MPa a = 2,5 mm ls = 417 mm
ls = 417 mm g=3mm b=17,9mm e= 7,1mm S11=28,86 kN kt=72 MPa	Zatem: ls = l1 + l2 → ls =3,5* l2 → Do obliczonych wartości l1o i l2o dodaje 2*a w celu uwzględnienia kraterów na końcach spoin, zatem rzeczywiste długości spoin wynoszą: l1 = l1o + 2*a l2 = l1o + 2*a 15.Określenie grubości spoiny Wymiar „a” wszystkich spoin łączących kątowniki L25x25x3 z blachą węzłową przymuje jako: a = 0,7*g a = 2,1 mm Ze względów technologicznych przyjmuje wysokość spoiny równą a = 2,5 mm dla obydwu kształtowników. 16.Określenie długości spoiny w prętach nr 1 i 10. Obliczam sumaryczną obliczeniową długość spoin, tzn. ls = l1 + l2 ; przypadającą na jeden kątownik. → Spoiny ułożone na krawędziach półki kątownika znajdują się w różnych odległościach od osi działania siły S. Dla zapewnienia równomiernego obciążenia obydwu spoin należy spełnić warunek: Zatem: ls = l1 + l2 → ls =3,5* l2 → l1 = ls-l2 = 148-42 Do obliczonych wartości l1o i l2o dodaje 2*a w celu uwzględnienia kraterów na końcach spoin, zatem rzeczywiste długości spoin wynoszą: l1 = l1o + 2*a l2 = l1o + 2*a 17. Obliczenie połączenia nitowego korony Z warunku na ścinanie nita: 22,5 mm	l1o= 298 mm l2o = 119 mm l1 = 303 mm l2 = 124 mm a= 2,5 mm dn=25 mm

12

---