Definicja ruchu.
Ruchem nazywamy zmianę położenia jednego ciała względem drugiego ciała lub układu ciał.
Prędkość średnia.
Prędkość średnia wyraża się stosunkiem całkowitej przebytej drogi do czasu, w którym tę drogę przebyto.
![]()
Vśr - prędkość średnia [m/s, km/h]
Sc - całkowita droga [m, km]
tc - całkowity czas [s, h]
Prędkość chwilowa.
Prędkość chwilowa jest to granica, do której dąży stosunek przyrostu drogi do przyrostu czasu, gdy przyrost czasu dąży do zera.
![]()
Vch - prędkość chwilowa [m/s, km/h]
S - przyrost drogi [m, km]
t - przyrost czasu [s, h]
Ruch jednostajny.
Ruch jednostajny jest to taki ruch, w którym wielkością stałą jest prędkość, a droga jest wprost proporcjonalna do czasu.
![]()
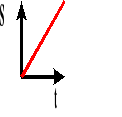
Prędkość wyraża się stosunkiem drogi do czasu.
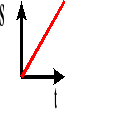
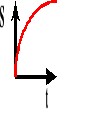
Wykres zależności drogi od czasu.
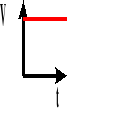
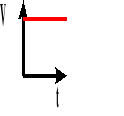
Wykres zależności prędkości od czasu.
V - prędkość [m/s, km/h]
S - droga [m, km]
t - czas [s, h]
Ruch jednostajnie przyspieszony.
Ruch jednostajnie przyspieszony jest to taki ruch, w którym w każdej sekundzie prędkość wzrasta o tą samą wartość. Wielkością stałą jest przyspieszenie.
![]()
Przyspieszeniem nazywamy stosunek przyrostu prędkości do czasu, w którym ten przyrost nastąpił.
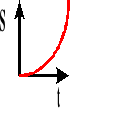
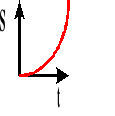
Wykres zależności drogi od czasu.
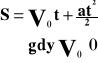
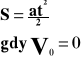
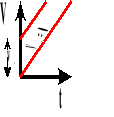
Wykres zależności prędkości od czasu.
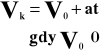
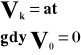
a - przyspieszenie [m/s2, km/h2]
V - przyrost prędkości [m/s, km/h]
t - czas [s, h]
S - droga [m, km]
V0 - prędkość początkowa [m/s, km/h]
Vk - prędkość końcowa [m/s, km/h]
Ruch jednostajnie opóźniony.
Ruch jednostajnie opóźniony jest to taki ruch, w którym w każdej sekundzie prędkość maleje o tą samą wartość.
![]()
Opóźnieniem nazywamy ujemny przyrost prędkości do czasu, w którym ten przyrost nastąpił.
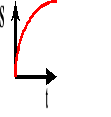
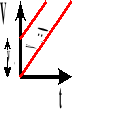
Wykres zależności drogi od czasu.
![]()
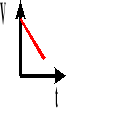
Wykres zależności prędkości od czasu.
![]()
a - opóźnienie [m/s2, km/h2]
V - przyrost prędkości [m/s, km/h]
t - czas [s, h]
S - droga [m, km]
V0 - prędkość początkowa [m/s, km/h]
Vk - prędkość końcowa [m/s, km/h]
I zasada dynamiki.
Gdy na ciało lub układ ciał nie działa żadna siła lub działające siły są w równowadze, to ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym.
II zasada dynamiki.
Gdy na ciało działa stała nie zrównoważona siła, to ciało porusza się ruchem jednostajnie przyspieszonym.
![]()
Przyspieszenie jest wprost proporcjonalne do działającej siły, a odwrotnie proporcjonalne do masy ciała.
a - przyspieszenie [m/s2, km/h2]
F - działająca siła [N=kg m/s2]
m - masa ciała [kg]
III zasada dynamiki.
Gdy ciało A działa na ciało B z pewną siłą, to ciało B działa na ciało A z taką samą siłą lecz przeciwnie skierowaną. Te dwie siły działają wzdłuż jednej prostej, są równe co do wartości bezwzględnej, lecz przyczepione są do dwóch różnych ciał. Układ nie może być w równowadze.
Jednostki siły układu SI.
Jednostki te wynikają ze wzoru na siłę:
![]()
1N jest to siła, która ciału o masie 1kg nadaje przyspieszenie 1m/s2.
![]()
1dyna jest to siła, która ciału o masie 1g nadaje przyspieszenie 1cm/s2.
![]()
F - działająca siła [dyna, N]
m - masa ciała [g, kg]
a - przyspieszenie [m/s2]
Jednostki siły układu ciężarowego.
![]()
W celu wyprowadzenia jednostki korzystamy ze wzoru.
1kG jest to siła, która ciału o masie 1 kg nadaje przyspieszenie ziemskie 9,81m/s2.
![]()
1G jest to siła, która ciału o masie 1g nadaje przyspieszenie ziemskie 9,81m/s2.
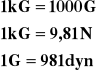
F - działająca siła [N, dyna]
m - masa ciała [g, kg]
a - przyspieszenie [m/s2]
P - działająca gramsiła (kilogramsiła) [G, kG]
g - przyspieszenie ziemskie [9,81m/s2]
Pęd.
Pęd jest to wektor o kierunku i zwrocie zgodnym z wektorem prędkości i liczbowo równy jest iloczynowi masy ciała i jego prędkości.
![]()
p - pęd [kg m/s]
m - masa ciała [kg]
V prędkość [m/s]
Popęd.
Popęd jest to wektor o kierunku i zwrocie zgodnym z wektorem siły i liczbowo równy jest iloczynowi siły i czasu.
![]()
- popęd [kg m/s]
F - działająca siła [N]
t - czas
Prawo zachowania pędu.
Z definicji przyspieszenia:
![]()
Z 2 zasady dynamiki:
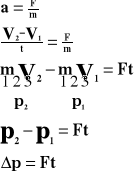
Przyrost pędu równy jest udzielonemu popędowi.
Jeżeli F=0 to p=0 - prawo zachowania pędu.
Gdy na ciało lub układ ciał nie działa żadna siła zewnętrzna lub działające siły są w równowadze, to ciało lub układ ciał nie zmienia swojego pędu.
a - przyspieszenie [m/s2]
V - przyrost prędkości [m/s]
t - czas [s]
F - działająca siła [N]
m - masa ciała [kg]
p - pęd [kg m/s]
Tarcie.
Tarcie zewnętrzne - siły występujące między powierzchniami stykających się ciał.
Tarcie kinetyczne - siła styczna do powierzchni przylegania i przeciwna do kierunku ruchu (np. ślizganie) jednego z tych ciał względem drugiego lub równoważąca zewnętrzne siły.
Tarcie statyczne - siła styczna do powierzchni przylegania ciał nieruchomych względem siebie.
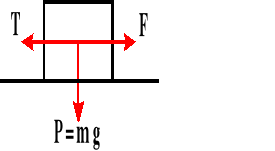
Ruch ciała po torze poziomym.
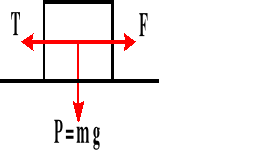
F<T - ciało stoi
F=T - ciało stoi lub porusza się ruchem jednostajnym prostoliniowym
F>T ciało porusza się ruchem jednostajnie przyspieszonym
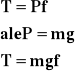
Na torze poziomym tarcie zależy wprost proporcjonalnie od ciężaru ciała i współczynnika tarcia.
Jeżeli ciało zostało wprowadzone w ruch z prędkością V (uzyskało energię kinetyczną) i w skutek działania siły tarcia zatrzymało się, to:
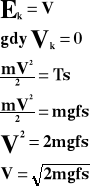
T - tarcie
F - siła
P - ciężar ciała
f - współczynnik tarcia
m - masa ciała
g - przyspieszenie ziemskie
Ek - energia kinetyczna
V - prędkość
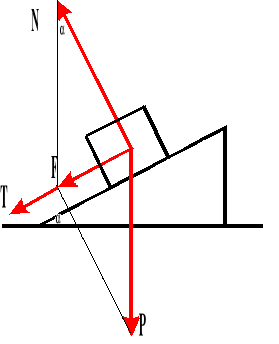
Ruch ciała pod górę równi pochyłej.
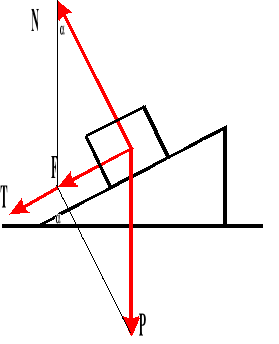
Gdy na ciało nie działa siła wciągająca, to ciało porusza się ruchem jednostajnie opóźnionym.
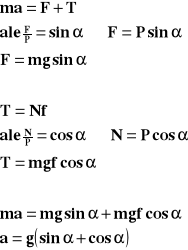
Powyższy wzór przedstawia wartość opóźnienia z jakim ciało porusza się pod górę równi pochyłej.
P - siła ciężkości
F - siła ściągania
T - siła tarcia
N - siła reakcji podłoża
m - masa ciała
a - opóźnienie
g - przyspieszenie ziemskie
f - współczynnik tarcia
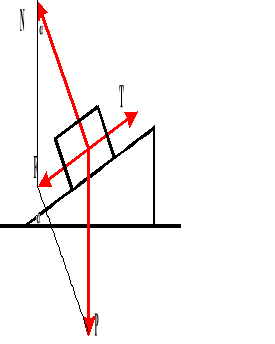
Ruch ciała w dół równi pochyłej.
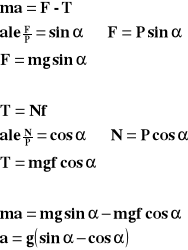
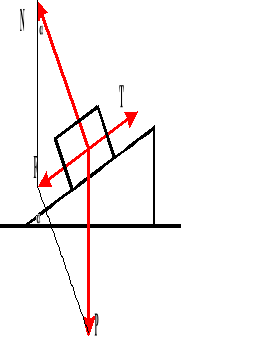
Powyższy wzór przedstawia wartość przyspieszenia z jakim ciało porusza się w dół równi pochyłej.
F<T - ciało stoi
F=T - ciało stoi lub porusza się ruchem jednostajnym prostoliniowym
F>T ciało porusza się ruchem jednostajnie przyspieszonym
P - siła ciężkości
F - siła ściągania
T - siła tarcia
N - siła reakcji podłoża
m - masa ciała
a - przyspieszenie
g - przyspieszenie ziemskie
f - współczynnik tarcia
Podstawowe pojęcia ruchu po okręgu.
Okresem nazywamy czas jednego pełnego obiegu.
![]()
Droga w tym czasie przebyta wynosi:
Częstotliwość jest to ilość obiegów przypadających na jednostkę czasu.
![]()
1Hz jest to taka częstotliwość, dla której w czasie 1s ciało dokonuje jednego obiegu.
Prędkość liniową obliczamy ze wzoru:
![]()
Prędkość kątowa wyraża się stosunkiem zakreślonego kąta do czasu, w którym ten kąt zakreślono.
![]()
Dla jednego okresu:
![]()
S - droga [m]
r - promień [m]
T - okres [s]
f - częstotliwość [Hz]
V - prędkość [m/s]
- prędkość kątowa [stopień/s]
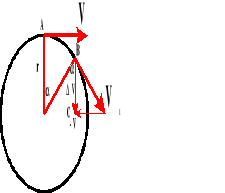
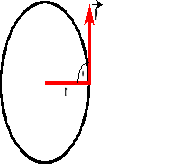
Przyspieszenie dośrodkowe.
![]()
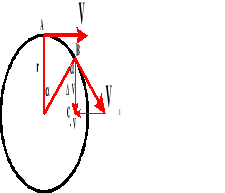
![]()
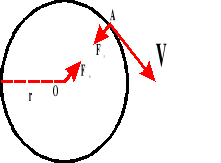
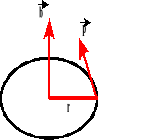
Bierzemy pod uwagę dwa trójkąty: OAB i BCD. Z rysunku wynika:
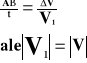
Dla małych kątów łuk AB równy jest odcinkowi.
Dzielimy licznik powyższej proporcji przez czas:
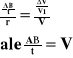
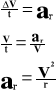
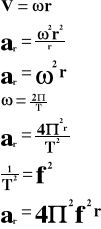
Wykorzystując wiadomości z tematu: „Podstawowe wiadomości o ruchu po okręgu”, wyprowadzamy wzór na przyspieszenie dośrodkowe:
ar - przyspieszenie dośrodkowe
AB - łuk
t - czas [s]
V - przyrost prędkości [m/s]
V1, V - prędkość [m/s]
r - promień [m]
T - okres [s]
f - częstotliwość [Hz]
- prędkość kątowa [stopień/s]
Siła dośrodkowa.
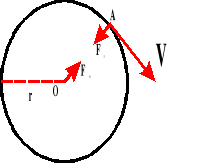
W ruchu po okręgu występują dwie siły:
Dośrodkowa Fr, która działa na ciało będące w tym ruchu;
Odśrodkowa F0, która działa na więzy.
Zgodnie z 1 zasadą dynamiki na ciało e tym ruchu musi działać siła.
Zgodnie z 2 zasadą dynamiki:
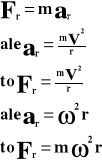
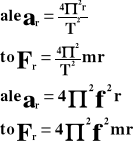
Fr - siła dośrodkowa [N]
F0 - siła odśrodkowa [N]
m - masa ciała [kg]
ar - przyspieszenie dośrodkowe
- prędkość kątowa [stopień/s]
r - promień [m]
T - okres [s]
f - częstotliwość [Hz]
V - prędkość [m/s]
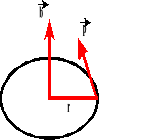
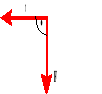
Reguła śruby prawoskrętnej.
Jeżeli śrubę prawoskrętną będziemy obracali zgodnie z kierunkiem ruchu ciała, to jej ruch postępowy wyznaczy nam kierunek i zwrot wektora momentu pędu.
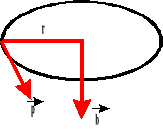
Moment pędu.
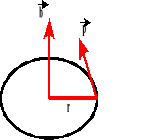
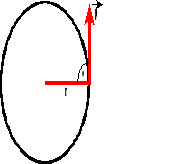
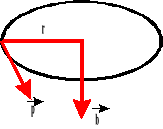
![]()
Moment pędu jest to wektor, którego kierunek i zwrot wyznacza reguła śruby prawoskrętnej.
Liczbowo moment pędu równy jest iloczynowi wektorowemu promienia wodzącego i pędu.
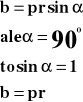
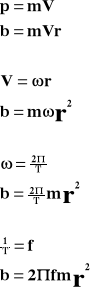
b - moment pędu
p - pęd
r - promień wodzący [m]
m - masa ciała [kg]
V - prędkość [m/s]
prędkość kątowa [stopień/s]
T - okres [s]
f - częstotliwość [Hz]
Zasada zachowania momentu pędu.
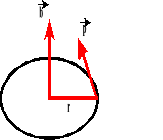
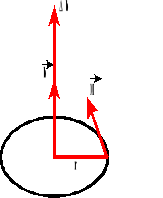
Gdy na ciało będące w ruchu po okręgu podziała moment siły, to ciało zmienia moment pędu.
![]()
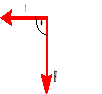
Moment siły jest to wektor, którego kierunek i zwrot wyznacza reguła śruby prawoskrętnej.
Liczbowo jest równy iloczynowi wektorowemu promienia wodzącego i działającej siły.
Jak wiemy przyrost pędu jest równy udzielonemu popędowi:
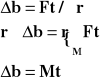
Gdy M=0, to b=0 - prawo zachowania momentu pędu.
Gdy na ciało będące w ruchu po okręgu nie działa moment siły, to ciało nie zmienia momentu pędu.
M - moment siły
r - promień wodzący [m]
F - działająca siła [N]
t - czas [s]
b - moment pędu
b - przyrost momenty pędu
Masa a ciężar właściwy. Gęstość a ciężar.
Ciężar jest wektorem (posiada punkt przyłożenia, kierunek działania, wartość i zwrot), a masa jest skalarem (liczbą). Masa dla danego ciała jest wielkością stałą (niezmienną), a ciężar zależy od przyspieszenia grawitacyjnego w danym punkcie.
![]()
Ciężar właściwy jest wektorem i też zależy od przyspieszenia grawitacyjnego w danym punkcie.
![]()
Ciężar właściwy wyraża się stosunkiem ciężaru ciała do jego objętości. Gęstość, czyli masa właściwa jest wielkością skalarną i dla danego ciała jest stała.
![]()
Gęstość wyraża się stosunkiem masy ciała do jego objętości.
![]()
P - ciężar ciała [G, kG]
m - masa ciała [g, kg]
g - przyspieszenie grawitacyjne
γ ciężar właściwy [G/cm3, kG/m3]
gęstość [kg/m3, g/mc3]
V - objętość [m3, cm3]
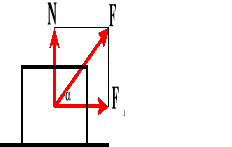
Praca.
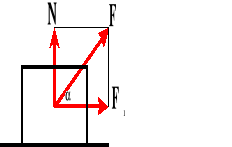
![]()
Praca wyraża się iloczynem siły przesuwającej ciało (równoległej do przesunięcia) i drogi, na której to ciało przemieszczono.
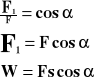
Siła wykonuje największą pracę wtedy, gdy jest równoległa do przesunięcia (=0, a cos0o=1).
![]()
1J jest to praca , którą wykonuje siła 1N na drodze 1m.
![]()
1erg jest to praca jaką wykonuje siła 1dyny na drodze 1cm.
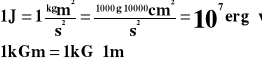
1kGm jest to praca, którą wykonuje 1kG na drodze 1m.
![]()
Jednostki pracy prądu:
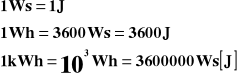
W - praca [J]
F - działająca siła [N]
s - droga [m]
- kąt
W - praca (dżul, kilogramometr)
Moc.
![]()
Moc wyraża się stosunkiem pracy do czasu, w którym ją wykonano.
1W jest to moc urządzenia, które w czasie 1s wykonuje pracę 1J.

M - moc [W]
W - praca [J]
t - czas [s]
Energia.
Energia jest to zasób pracy „nagromadzony” w ciele, która przez to ciało może być zwrócona.
Energia kinetyczna.
![]()
Energia kinetyczna jest to zasób pracy nagromadzony w ciałach będących w ruchu. Energia kinetyczna zależy wprost proporcjonalnie od masy ciała i kwadratu prędkości.
Ek - energia kinetyczna [J]
M - masa ciała [kg]
V - prędkość [m/s]
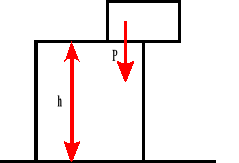
Energia potencjalna wysokości.
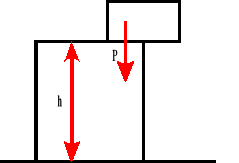
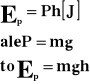
Energia potencjalna wysokości jest to zasób pracy nagromadzony w ciałach podniesionych na pewną wysokość. Energia potencjalna wysokości zależy wprost proporcjonalnie od ciężaru ciała i wysokości na jaką to ciało podniesiono.
Ep - energia potencjalna [J]
P - ciężar ciała
m - masa ciała [kg]
h - wysokość [m]
Energia potencjalna sprężystości.
![]()
Energia potencjalna sprężystości jest to zasób pracy nagromadzony w ciałach sprężystych i odkształconych o odcinek x.
Ep - energia potencjalna [J]
k - współczynnik sprężystości
x - wychylenie
Spadek swobodny.
Wszystkie ciała podniesione na pewną wysokość i puszczone swobodnie, poruszają się ruchem jednostajnie przyspieszonym z przyspieszeniem ziemskim.
Przebytą wysokość obliczamy ze wzoru:
![]()
A prędkość końcową:
![]()
Ponieważ ciało będące na wysokości posiada energię potencjalną, która tuż przy ziemi zamienia się na energię kinetyczną, to z tego faktu możemy obliczyć prędkość końcową:
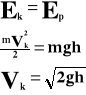
h - wysokość [m]
g - przyspieszenie ziemskie [9,81m/s2]
t - czas [s]
Vk - prędkość końcowa [m/s]
m - masa ciała [kg]
Rzut pionowy do góry.
Wszystkie ciała rzucone pionowo do góry poruszają się ruchem jednostajnie opóźnionym z opóźnieniem ziemskim.
Przebytą wysokość obliczamy ze wzoru:
![]()
A prędkość w dowolnym czasie:
![]()
Gdy ciało osiągnie wysokość maksymalną, wtedy energia kinetyczna zmienia się w energię potencjalną.
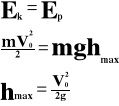
h - wysokość [m]
V0 - prędkość początkowa [m/s]
Vk - prędkość końcowa [m/s]
t - czas [s]
g - opóźnienie ziemskie [9,81m.s2]
Ek - energia kinetyczna [J]
Ep - energia potencjalna [J]
Rut pionowy w dół.
Wszystkie ciała rzucone pionowo w dół poruszają się ruchem jednostajnie przyspieszonym z przyspieszeniem ziemskim.
![]()
Przebytą wysokość obliczamy ze wzoru:
W momencie rzucenia ciało posiada energię całkowitą, równą sumie energii potencjalnej i kinetycznej.
![]()
Tuż przy powierzchni ziemi energia całkowita zamienia się w energię kinetyczną.
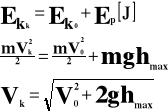
h - wysokość [m]
Ec - energia całkowita [J]
Ep - energia potencjalna [J]
Ek - energia kinetyczna [J]
V0 - prędkość początkowa [m/s]
Vk - prędkość końcowa [m/s]
g - przyspieszenie ziemskie [m/s2]
t - czas [s]
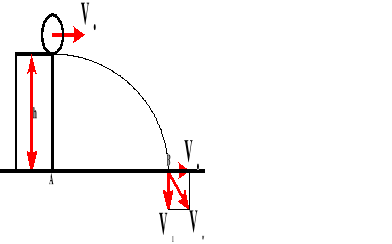
Rut poziomy.
Rut poziomy to po prostu rzut w kierunku poziomym.
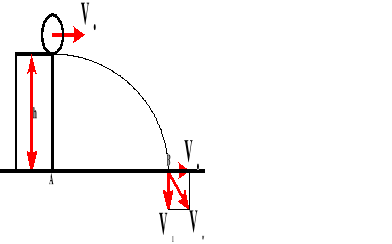
Rzut poziomy jest ruchem złożonym i składającym się z dwóch ruchów:
Jednostajnego w ruchu poziomym;
Spadku swobodnego.
Wysokość obliczamy ze wzoru:
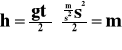
A czas:
![]()
Zasięg rzutu obliczamy z ruchu jednostajnego:
![]()
Prędkość wypadkową obliczamy z twierdzenia Pitagorasa:
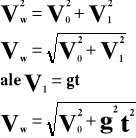
h - wysokość [m]
g - przyspieszenie ziemskie [m/s2]
t - czas [s]
AB - zasięg rzutu [m]
V0 - prędkość początkowa [m/s]
Vk - prędkość końcowa [m/s]
Vw - prędkość wypadkowa [m/s]
Rzut ukośny.
Rzut ukośny jest ruchem złożonym i składa się z:
W pierwszej fazie:
Rzutu pionowego do góry;
Ruchu jednostajnego w kierunku poziomym;
W drugiej fazie:
Ruchu jednostajnego w kierunku poziomym;
Spadku swobodnego.
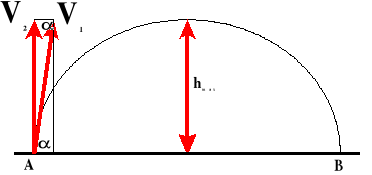
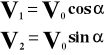
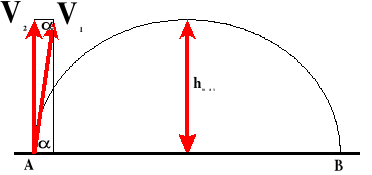
W obliczeniu wysokości maksymalnej decydującą ideę odgrywa druga prędkość, która na maksymalnej wysokości jest równa zero.
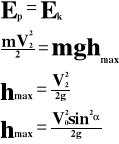
Całkowity czas trwania rzutu składa się z sumy czasów:
Wyrzucenia;
Spadania.
Te czasy są sobie równe.
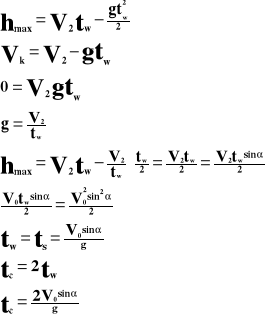
W kierunku poziomym ciało porusza się ruchem jednostajnym, a więc na zasięg rzutu ma wpływ całkowity czas trwania rzutu i składowy wektor pierwszej prędkości:
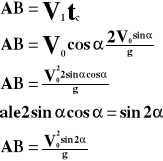
h - wysokość [m]
g - przyspieszenie ziemskie [m/s2]
Tc - całkowity czas [s]
Tw - czas wyrzutu [s]
Ts - czas spadania [s]
Ek - energia kinetyczna [J]
Ep - energia potencjalna [J]
V1, V2 - prędkości [m/s]
V0 - prędkość początkowa [m/s]
AB - zasięg rzutu [m]
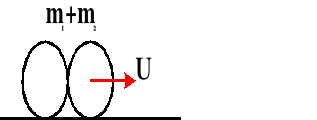
Zderzenia niesprężyste.
W tych zderzeniach biorą udział ciała niesprężyste. W tych zderzeniach spełnione jest prawo zachowania pędu, tzn. że suma pędów przed zderzeniem równa jest sumie pędów po zderzeniu. Nie jest zachowane prawo zachowania energii kinetycznej, bo w trakcie zderzenia część energii zostaje zużyta na odkształcenie trwałe ciała i energia kinetyczna po zderzeniu jest mniejsza niż przed zderzeniem.
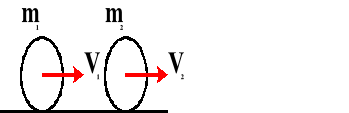
Przed zderzeniem:
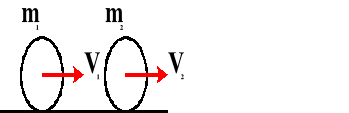
Po zderzeniu:
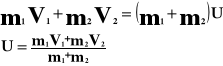
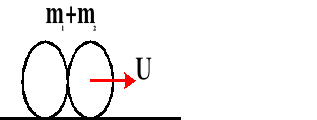
m1 - masa pierwszego ciała [kg]
m2 - masa drugiego ciała [kg]
V1 - prędkość pierwszego ciała przed zderzeniem [m/s]
V2 - prędkość drugiego ciała przed zderzeniem [m/s]
U - prędkość wspólna obu ciał po zderzeniu [m/s]
Zderzenia sprężyste.
W zderzeniach sprężystych biorą udział ciała sprężyste.
Spełnione są dwa prawa:
Prawo zachowania pędu - suma pędów przed zderzeniem równa się sumie pędów po zderzeniu;
Prawo zachowania energii kinetycznej - suma energii kinetycznych przed zderzeniem równa się sumie energii kinetycznych po zderzeniu.
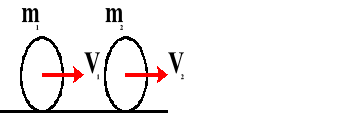
Przed zderzeniem:
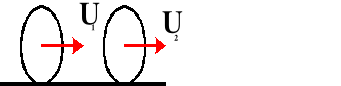
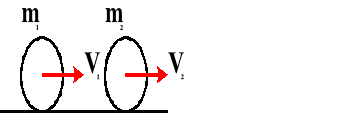
Po zderzeniu
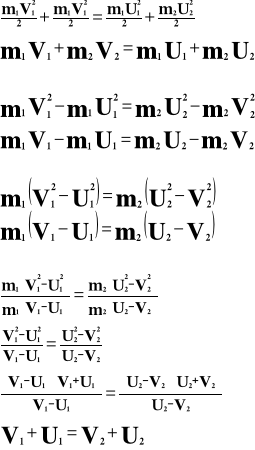
Suma prędkości przed zderzeniem i po zderzeniu jednego ciała równa jest sumie prędkości przed i po zderzeniu drugiego ciała.
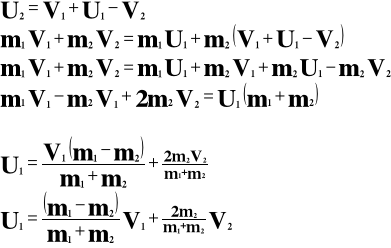
Analogicznie:
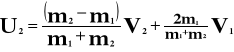
m1 - masa pierwszego ciała [kg]
m2 - masa drugiego ciała [kg]
V1 - prędkość pierwszego ciała przed zderzeniem [m/s]
V2 - prędkość drugiego ciała przed zderzeniem [m/s]
U1 - prędkość pierwszego ciała po zderzeniu [m/s]
U2 - prędkość drugiego ciała po zderzeniu [m/s]
Mechanika
Mechanika
36
35
![]()
![]()
![]()
![]()
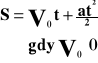

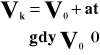
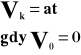
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
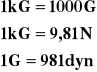
![]()
![]()
![]()
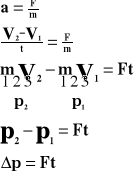
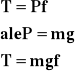
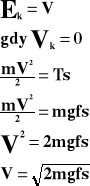
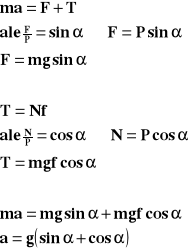
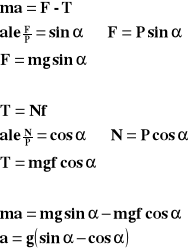
![]()
![]()
![]()
![]()
![]()
![]()
![]()
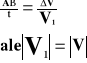
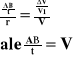
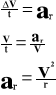
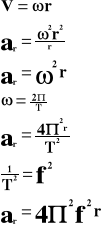
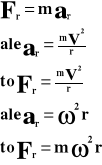
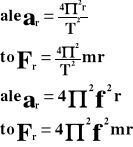
![]()
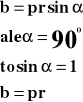
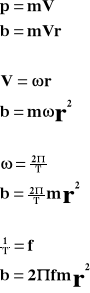

![]()
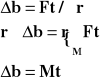
![]()
![]()
![]()
![]()
![]()
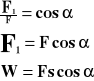
![]()
![]()
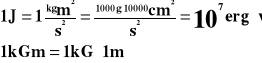
![]()
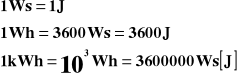
![]()

![]()
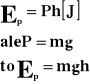
![]()
![]()
![]()
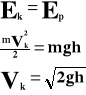
![]()
![]()
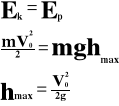
![]()
![]()
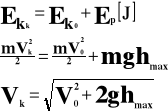
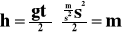
![]()
![]()
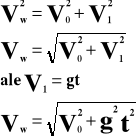
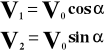
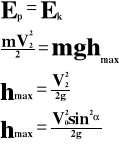
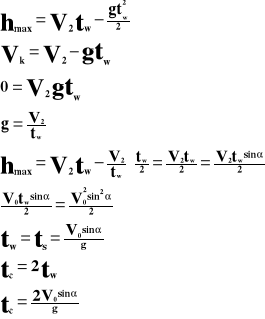
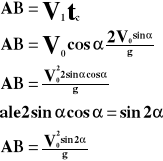
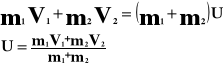
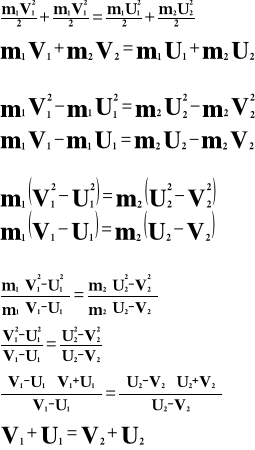
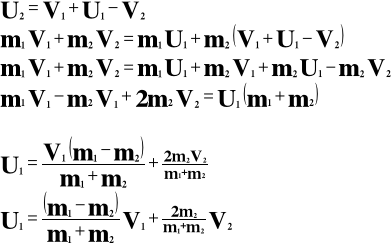
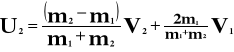
Wyszukiwarka
Podobne podstrony:
SPRAWOZDANIE NR 1, ZiIP, II Rok ZIP, Metrologia, Sprawozdanie nr 1
metrologia - błędy kształtu, ZiIP, II Rok ZIP, Metrologia, metrologia, Sprawozdania
metrologia Sprawozdanie 2
Sprawozdanie Metrologia ćw 3
Metrologia ćw 5 sprawozdaniez
Sprawozdanie metrologia cw17
metrologia Sprawozdanie 1
metrologia Sprawozdanie 5
metrologia Sprawozdanie 4
Zastosowanie kompesatorów prądu stałego v3, Politechnika Lubelska, Studia, Studia, Sprawozdania, ME
Metrologia - sprawozdania, Metrologia
20'', Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozdania, Lab
charakterystyki 2 2, Mechatronika AGH IMIR, rok 2, Metrologia sprawozdania, inncyh
metr-koło 4, Mechatronika AGH IMIR, rok 2, Metrologia sprawozdania, inncyh
Metrologia Spraw-4, Metrologia--sprawozdania
14'''''''''', Politechnika Lubelska, Studia, semestr 5, Sem V, Sprawozdania, sprawozdania, Sprawozda
metrologia Sprawozdanie 3 popr
Sprawozdanie Bunsch Metrologia
metrologia Sprawozdanie 2
metrologia sprawozdanie cwiczenie 3
więcej podobnych podstron