Połączenia śrubowe i gwintowe
Wprowadzenie
Połączenia śrubowe oraz gwintowe są połączeniami rozłącznymi, zaliczanymi do grupy połączeń kształtowo-ciernych, w których to połączeniach jednocześnie wykorzystywane są siły spójności materiału, z jakiego wykonane są elementy złącza oraz siły tarcia występujące na powierzchni przylegania gwintu zewnętrznego (śruby) i wewnętrznego (nakrętki) najczęściej zabezpieczające jedynie złącze przed samoczynnym luzowaniem.
Mianem połączeń śrubowych określa się połączenia pośrednie, realizacja których wymaga stosowania łączników w postaci śrub, wkrętów bądź też śrub i nakrętek.
Pojęciem połączenie gwintowe opisuje się natomiast połączenie bezpośrednie, w którym gwinty śruby i nakrętki wykonane są wprost na łączonych elementach.
Gwintem nazywa się obszar ograniczony boczną powierzchnią walca lub stożka jako powierzchnia odniesienia i powierzchnią gwintową.
Wykonując na walcu lub otworze walcowym bruzdę o stałym przekroju, przebiegającą wzdłuż określonej linii śrubowej walcowej otrzymuje się gwint walcowy zewnętrzny lub wewnętrzny.
Powierzchnią gwintową jest powierzchnia gwintu i bruzdy.
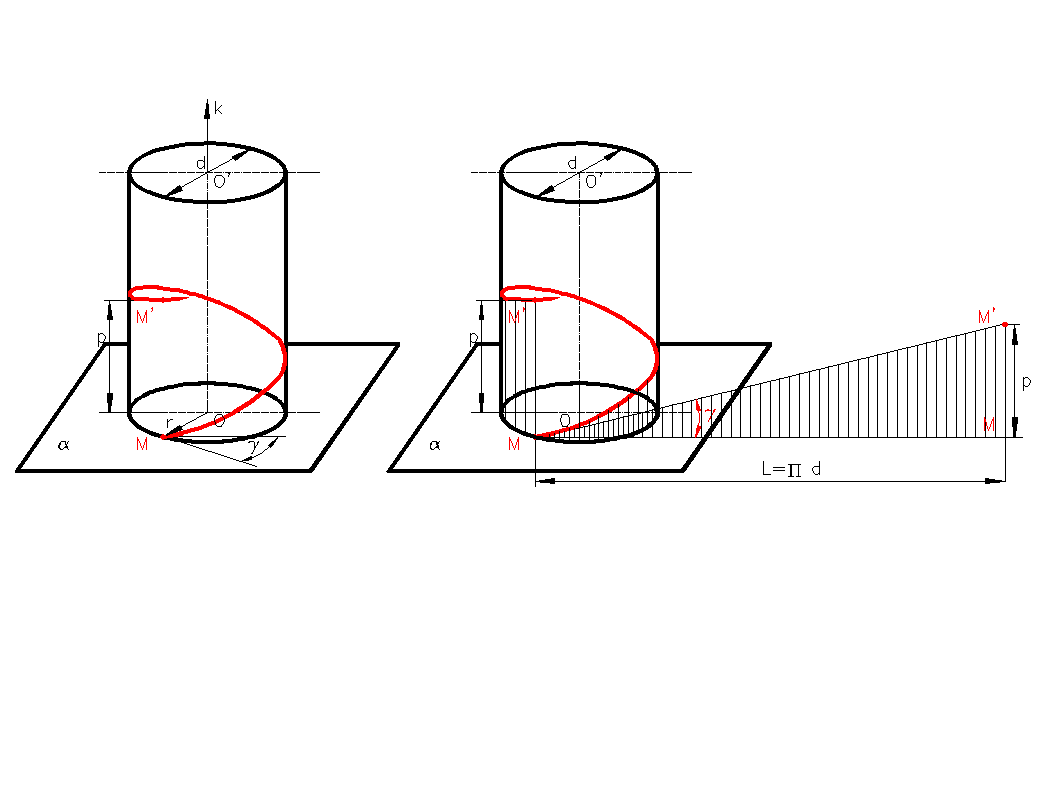
Rys. 1. Linia śrubowa walcowa i jej rozwinięcie na płaszczyźnie
Linia śrubowa walcowa jest to tor punktu /M/ wykonującego ruch obrotowy wokół punktu /O/ leżącego na płaszczyźnie /α/ przesuwającego się wzdłuż prostej /k/ prostopadłej do płaszczyzny.
Powstawanie tej linii ilustruje Rys.1.
Odległość /p/, o jaką przesuwa się płaszczyzna / α / na jeden pełny obrót punktu /M/ dookoła środka /O/ jest skokiem linii śrubowej.
Skok /p/ jest wielkością stałą jeżeli zachowany jest stały stosunek prędkości kątowej punktu /M/ dookoła punktu /O/ do prędkości przesuwania się płaszczyzny / α/.
Linia śrubowa o skoku /p/ opisana na walcu o średnicy /d/ w rozwinięciu na płaszczyznę tworzy prostą nachyloną pod kątem /γ/ do podstawy.
Kąt ten określa się mianem kąta nachylenia linii gwintowej i wyznacza z zależności:
![]()
Zarys i oznakowanie gwintów normalnych
Linia konturowa powstała w wyniku przecięcia powierzchni gwintowej płaszczyzną przechodzącą przez oś gwintu tworzy zarys gwintu.
W zależności od kształtu zarysu podstawowego rozróżnia się gwinty: trójkątne, trapezowe symetryczna i niesymetryczne, okrągłe i prostokątne /do celów specjalnych stosowane są również inne gwinty np. gwint rurowy/.
Zarysy odniesienia, w większości, objęte są przepisami normalizacyjnymi.
Znormalizowane są również: nominalna średnica gwintu, skok gwintu oraz kąt rozwarcia zarysu.
Pozostałe wymiary zarysów powiązane są z wartością skoku i średnicy nominalnej.
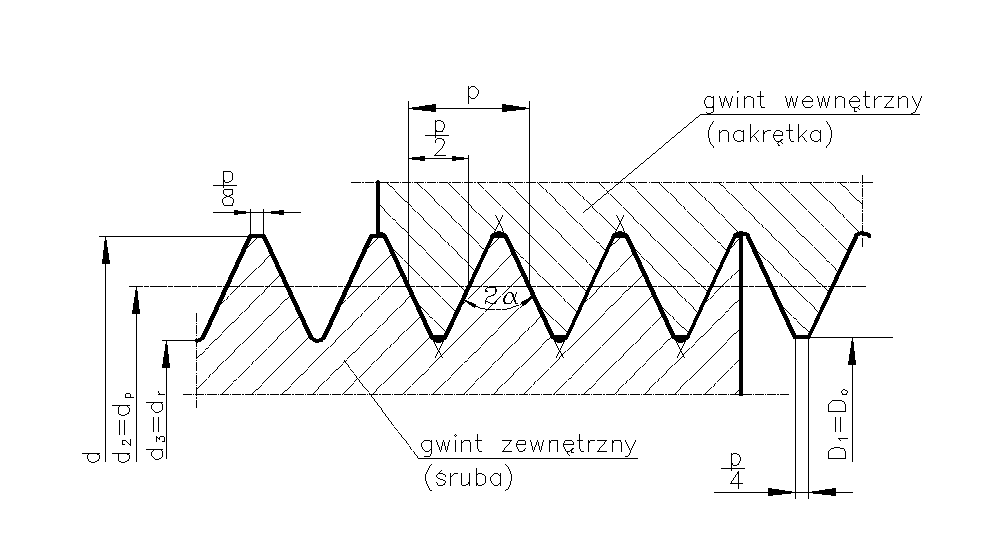
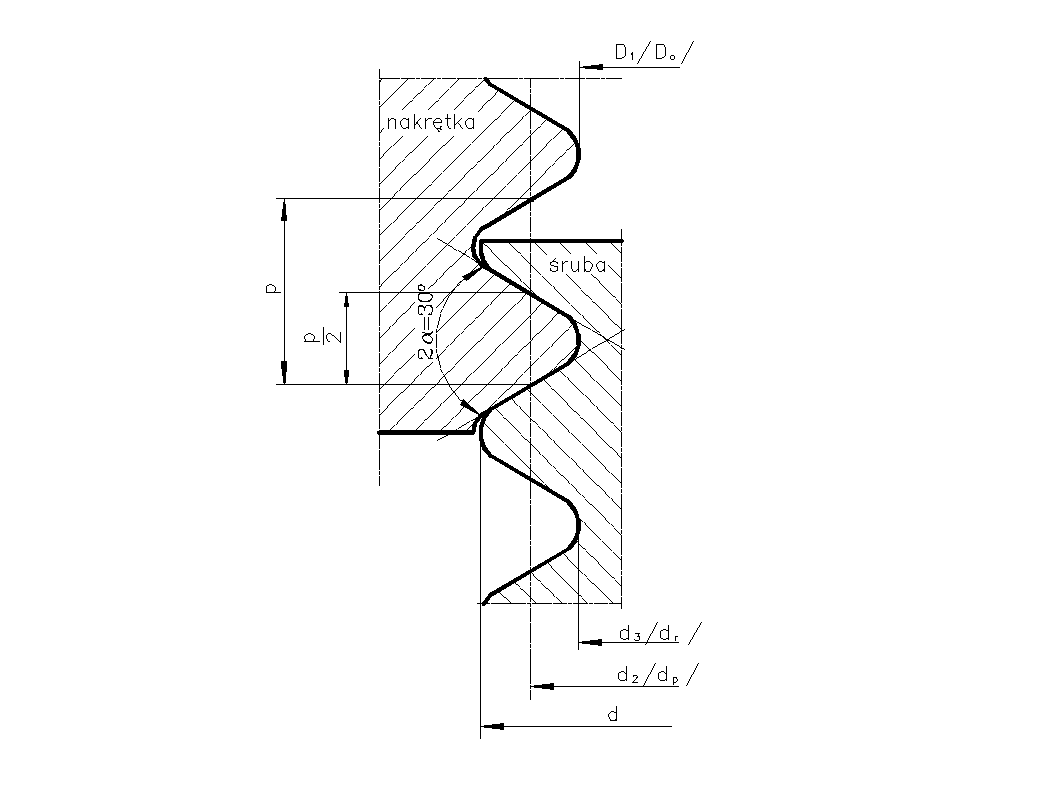
Rys. 2. Wymiary gwintu trójkątnego
gdzie:
d - średnica zewnętrzna (nominalna) śruby,
d2 /dp/ - średnica podziałowa gwintu śruby,
D1 /Do/ - średnica otworu w nakrętce,
d3 /dr/ - średnica rdzenia śruby,
α / 2 α / - kąt zarysu gwintu /kąt rozwarcia/,
p - podziałka gwintu.
Podziałką gwintu /p/ nazywa się odległość sąsiednich zwojów mierzoną na zarysie gwintu wzdłuż osi.
Dla gwintów jednokrotnych podziałka gwintu równa jest jego skokowi.
Skok gwintu stanowi przesunięcie zarysu zwoju wzdłuż osi po pełnym jego obrocie /skok jest wielkością wymiarową mierzoną na średnicy podziałowej/.
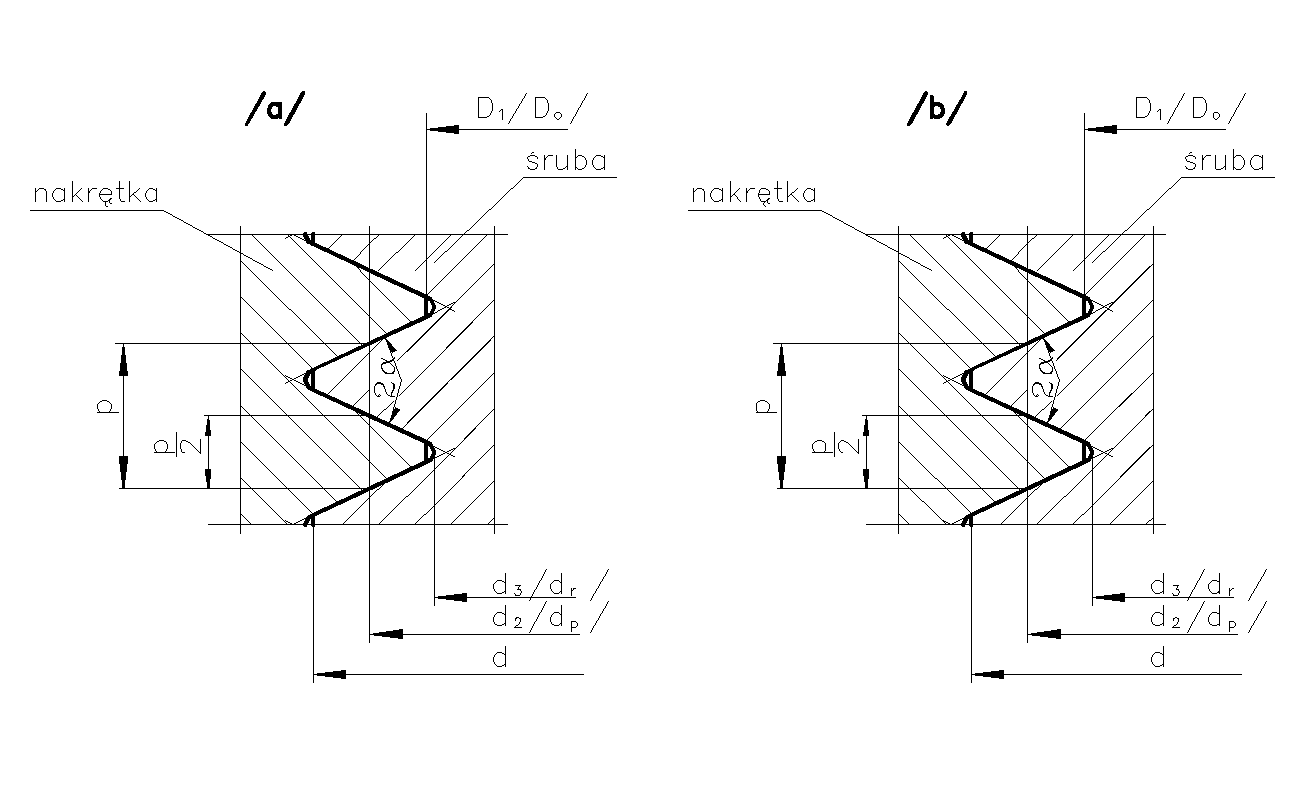
Rys. 3. Gwint trójkątny metryczny /a/ i calowy /b/
Oznaczenie gwintu metrycznego ISO /wg PN-ISO 724/ gwint trójkątny metryczny o średnicy nominalnej d=30mm, skoku gwintu p=2mm i kącie zarysu 2![]()
=60o
Oznaczenie:
M30x2
Oznaczenie gwintu calowego /wg PN-ISO 68-2/ gwint trójkątny calowy o średnicy nominalnej d=1” i kącie zarysu 2![]()
=55o .
Skok w oznaczeniu gwintu Whitworta ![]()
mm gdzie i - liczba skoków na jeden cal.
Oznaczenie:
1” x 1/6”
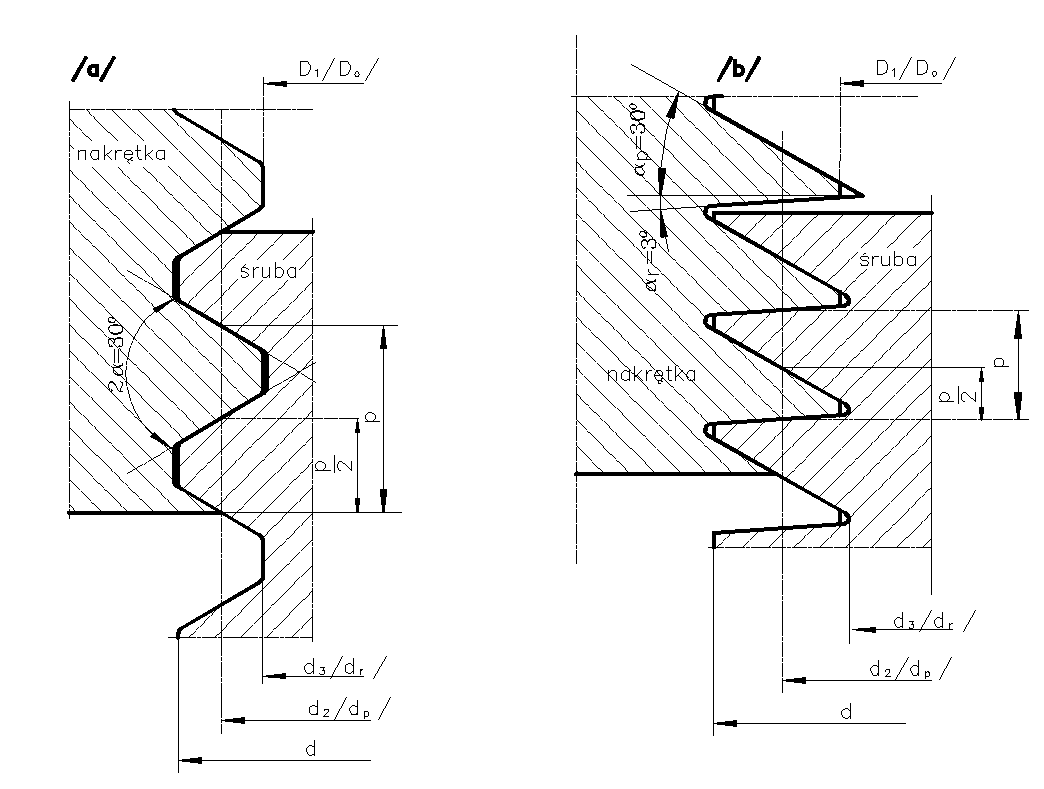
Rys.4. Gwint trapezowy symetryczny /a/ i niesymetryczny /b/
Oznaczenie gwintu trapezowego symetrycznego /wg PN-ISO 2904/ gwint trapezowy symetryczny o kącie rozwarcia zarysu 2α=30o, średnicy nominalnej d=52mm i skoku p=14mm.
Oznaczenie:
Tr52x14
Oznaczenie gwintu trapezowego niesymetrycznego /wg PN-88/M-02019 gwint trapezowy niesymetryczny o kącie pomocniczym αp=30o i kącie roboczym αr=3o, średnicy nominalnej d=80mm i skoku p=10mm.
Oznaczenie:
S80x10
Rys. 5. Gwint okrągły
Oznaczenie gwintu okrągłego o kącie zarysu 2α=30o średnicy d=1” i skoku ![]()
mm (gdzie /i/ jest liczbą skoków na 1”).
Oznaczenie:
Rd 1” x 1/6”
Obliczenia połączeń śrubowych
Tarcie w złączu śrubowym
W celu wyznaczenia związków między siłami działającymi na gwint rozwijamy go na płaszczyznę i rozpatrujemy jak równię pochyłą. Kąt pochylenia równi jest równy średniemu kątowi pochylenia gwintu /![]()
/. Ruch nakrętki obciążonej siłą Q pod działaniem siły obwodowej H równoważyć możemy jako ruch klocka (wycinka nakrętki) obciążonego siła Q po równi pochyłej pod działaniem siły Hp przy podnoszeniu i siły Ho przy opuszczaniu.
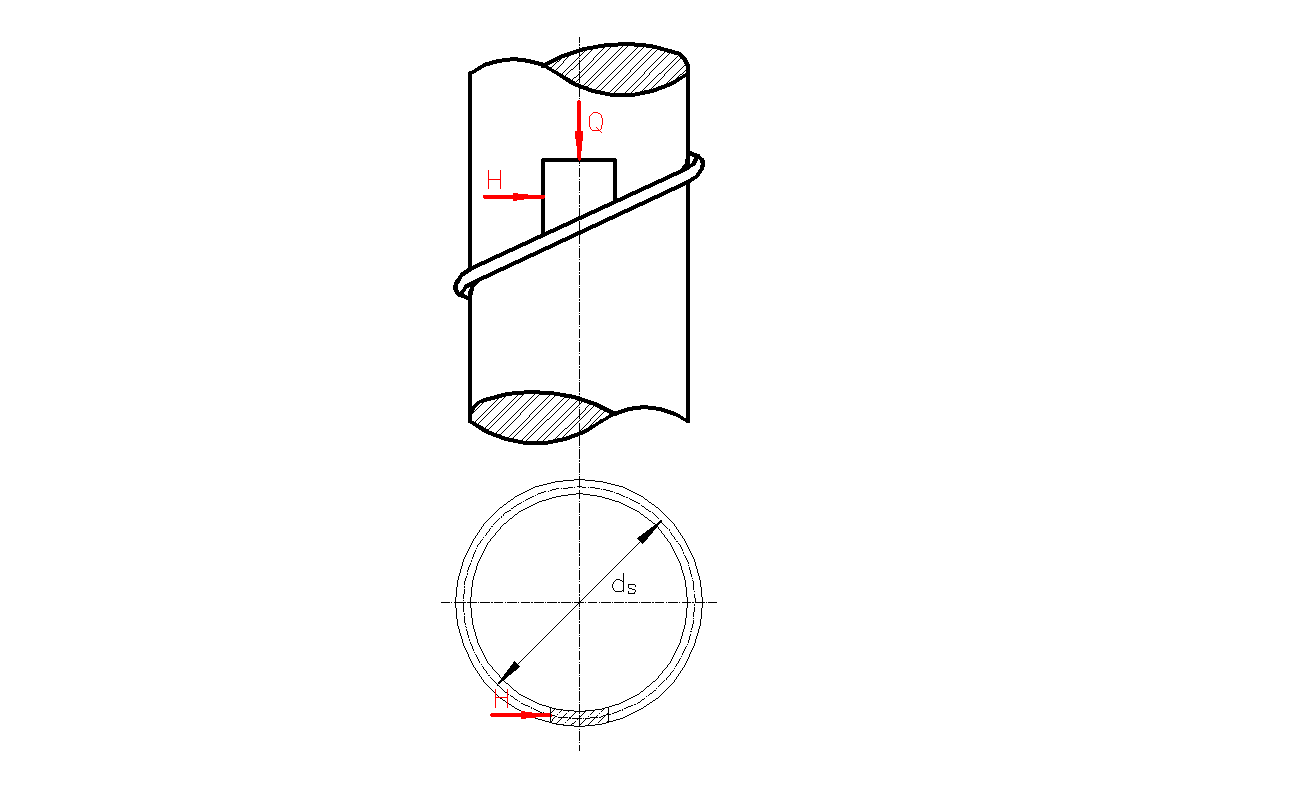
Rys. 6. Ruch nakrętki obciążonej siłą Q pod działaniem siły obwodowej H
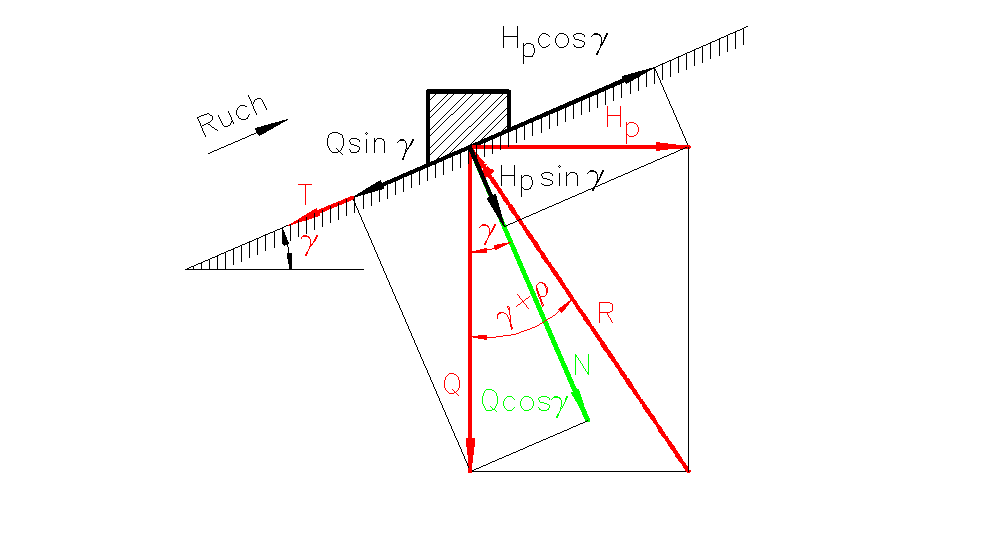
Rys. 7. Rozkład sił przy napinaniu-podnoszeniu
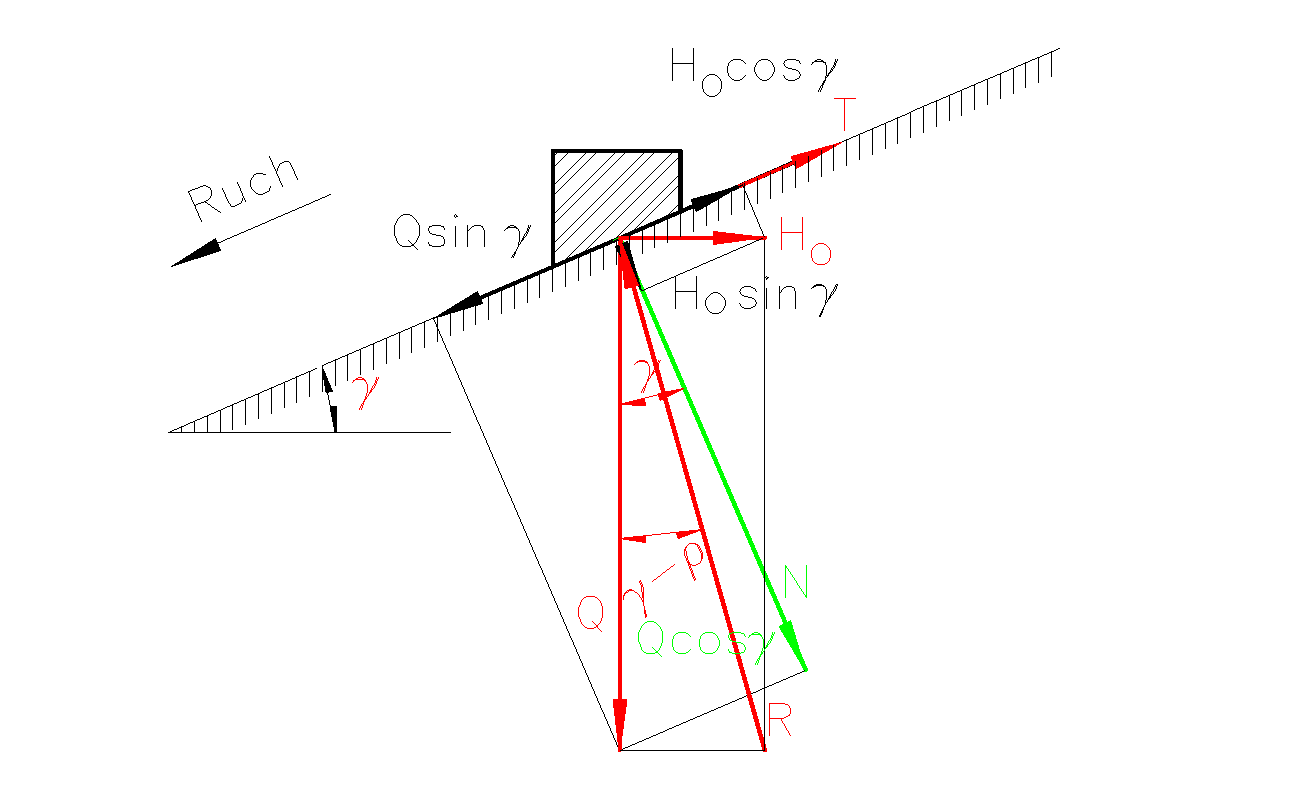
Rys. 8. Rozkład sił przy luzowaniu-opuszczaniu
Przy zamierzonym ruchu klocka po równi pochyłej w górę (Rys. 8) reakcja R odchyli się od normalnej do powierzchni styku o kąt tarcia ![]()
w kierunku ruchu. Kąt zawarty między kierunkiem siły Q i reakcją R wynosi ![]()
.
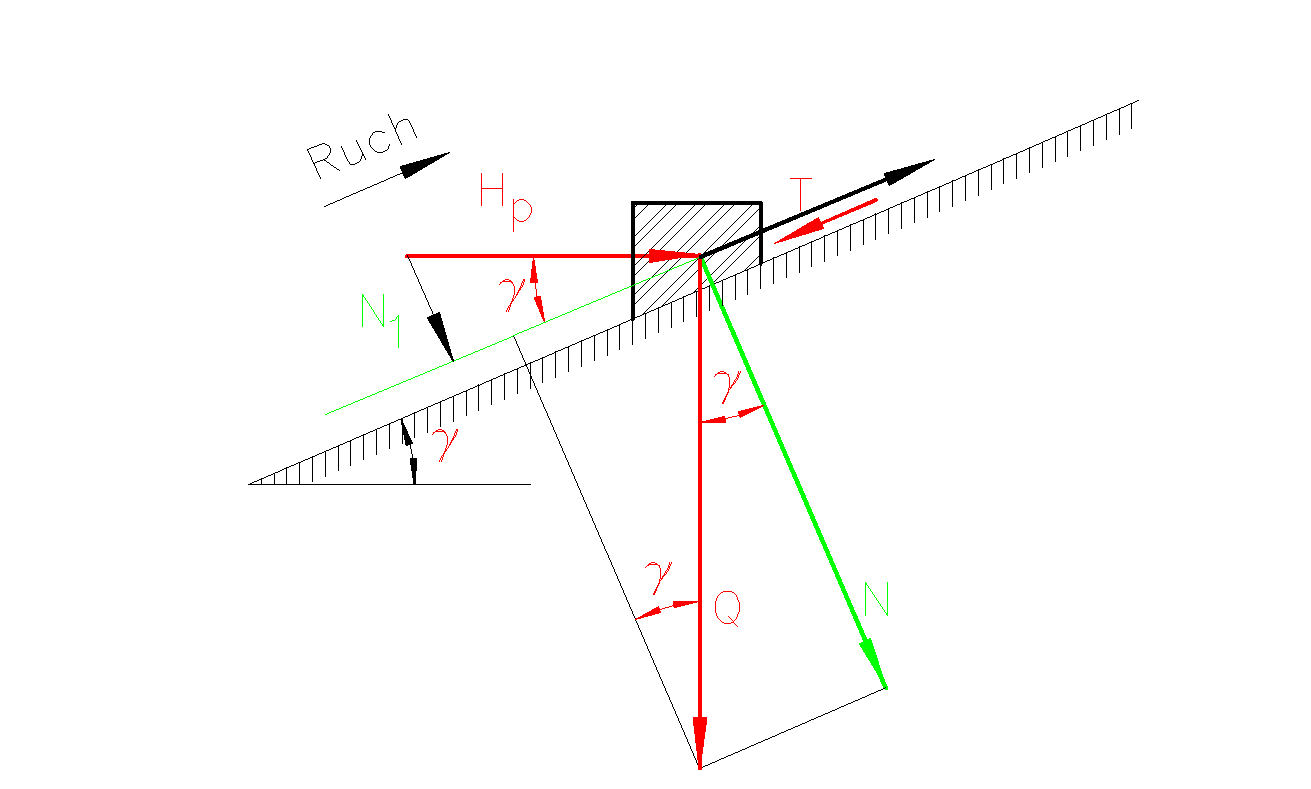
Rys. 9. Rozkład sił przy ruchu klocka w górę
Siłę obwodową przy podnoszeniu nakrętki Hp można wyznaczyć z warunku równowagi sił w kierunku równoległym do równi:
![]()
gdzie:
![]()
po podstawieniu
![]()
![]()
![]()
dzielimy licznik i mianownik przez cos![]()
![]()
podstawiamy ![]()
![]()
- kąt tarcia
![]()
![]()
Kąt jaki tworzy reakcja R przy ruchu nakrętki w dół wynosi ![]()
.
Siła obwodowa przy opuszczaniu nakrętki Ho wynosi:
![]()
Jeżeli część robocza zarysu gwintu tworzy kąt ![]()
( 2![]()
- kąt zarysu gwintu) z płaszczyzną prostopadłą do osi śruby (Rys. 10) to wzór
![]()
przybierze nieco inną postać, ponieważ przy tej samej sile Q wzrośnie siła tarcia przeciwdziałająca względnemu ruchowi śruby i nakrętki.
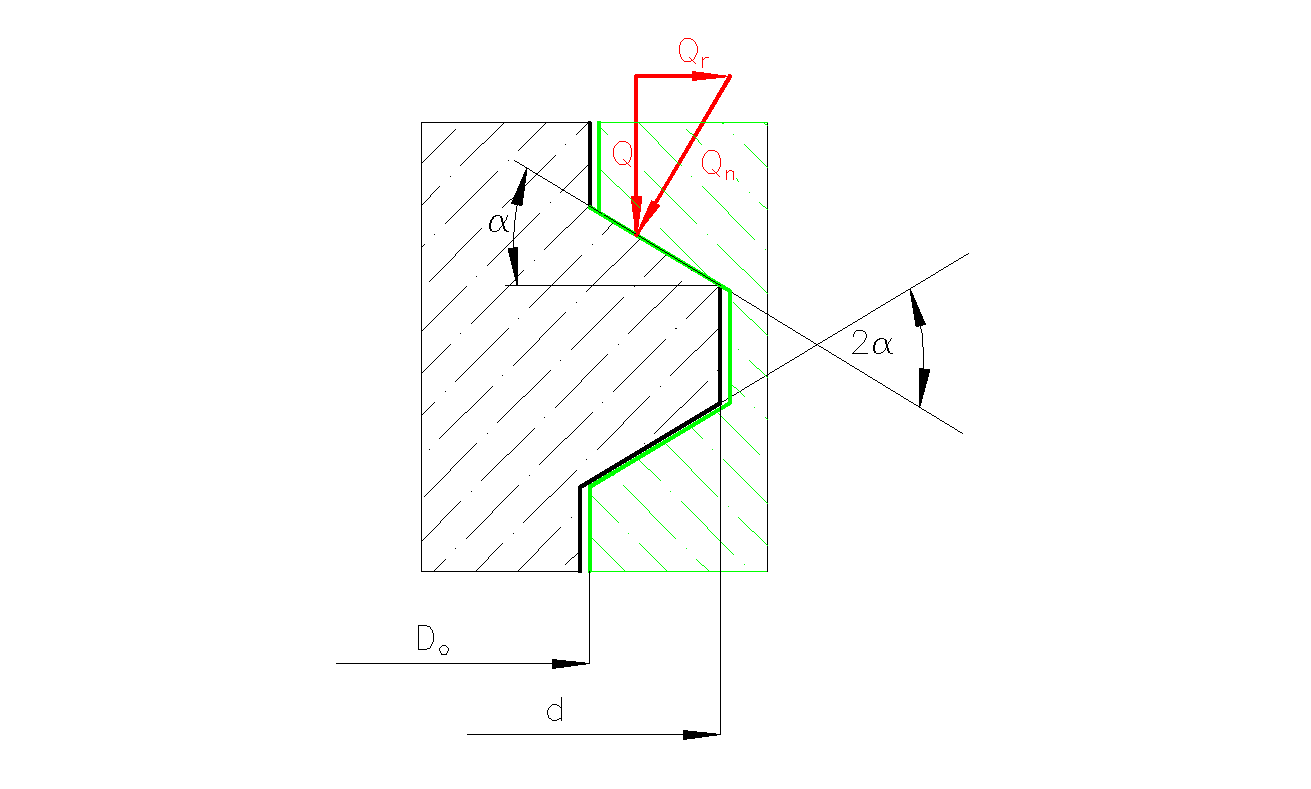
Rys.10. Rozkład siły Q na składowe normalną i promieniową
Siłę Q działającą równolegle do kierunku osi śruby możemy rozłożyć na składową Qn normalna do powierzchni roboczej gwintu i składową promieniową Qr (obie rozłożone równomiernie na całej powierzchni roboczej gwintu). Siła tarcia jest w tym przypadku równa
![]()
Wielkość ![]()
nazywamy pozornym współczynnikiem tarcia ![]()
- odpowiada jej pozorny kąt tarcia ![]()
![]()
Wzór na siłę obwodową H przy opuszczaniu lub podnoszeniu nakrętki przyjmie postać
![]()
Moment tarcia na gwincie wywołany przez siłę obwodową H wynosi
![]()
gdzie:
![]()
- średnia średnica gwintu
Jest zrozumiałe, że gwinty służące do łączenia części maszyn powinny być samohamowne, tzn. że powinien być spełniony warunek ![]()
.
Oznacza to, że pozorny kąt tarcia ![]()
powinien być jak największy, czyli przy stałym kącie tarcia ![]()
kąt ![]()
powinien być jak największy. Dlatego też śruby złączne wykonuje się z gwintem trójkątnym (2![]()
= 60o).
Śruby służące do napędzania części maszyn - śruby ruchowe - przenoszące moc konstruuje się z myślą o osiągnięciu przez nie jak największej sprawności. Te śruby wykonuje się z gwintem prostokątnym lub z gwintem trapezowym (mającym większą wytrzymałość).
Sprawność gwintu
Sprawnością ![]()
nazywamy stosunek pracy uzyskanej do pracy włożonej
![]()
W mechanizmie śrubowym przy podnoszeniu w czasie jednego obrotu praca uzyskana
![]()
![]()
![]()
![]()
praca włożona Lw zużyta na pokonanie siły biernej Q i oporów (tarcie w gwincie) jest równa
![]()
![]()
stąd sprawność gwintu
![]()
![]()
Optymalna wartość kąta pochylenia gwintu wynika z warunku![]()
i wynosi
![]()
zaś maksymalna sprawność połączenia
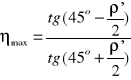
Łączniki śrubowe, które winny być samohamowne mają sprawność ![]()
mniejszą od 50%, kąt nachylenia gwintu ![]()
= 4o÷6o podnośniki, ![]()
= 1,5o÷5o śruby.
Złącza ruchowe natomiast powinny mieć sprawność jak największą (od 75% do 80%). Kąt pochylenia gwintu ![]()
= 18o÷25o (np. w prasach). Najwyższą sprawność można osiągnąć przy gwincie trapezowym niesymetrycznym, gdy obciążenie przenosi jego bok o kącie zarysu powierzchni roboczej ![]()
=3o.
Przy napinaniu śruby obok tarcia na gwincie wystąpi tarcie na powierzchni oporowej nakrętki, daje moment tarcia MT
![]()
gdzie:
![]()
- średnia średnica powierzchni styku śruby i nakrętki;
![]()
- współczynnik tarcia między powierzchniami nieruchomego przedmiotu i ruchomej śruby (nakrętki).
Sumaryczny moment tarcia występujący w złączu podczas dokręcania wynosi:
![]()
![]()
Przy napinaniu śruby nakrętką moment ![]()
musi być zrównoważony momentem ![]()
siły przyłożonej na klucz
![]()
[Nm]
gdzie
![]()
- siła ręki w [Nm];
![]()
- czynna długość klucza.
Obliczanie połączeń gwintowych
Projektowanie połączenia gwintowego polega na ustalaniu wymiarów łączników:
- przekroju rdzenia śruby,
- wysokości nakrętki,
- oraz sprawdzeniu wytrzymałości gwintu.
Dokładne obliczenia wytrzymałości gwintu jest niemożliwe, ponieważ rozkład nacisków na gwincie zarówno w kierunku promieniowym jak i osiowym jest nierównomierny. Warunek równomierności rozkładu nacisków na poszczególne zwoje gwintu jest spełniony tylko wtedy, gdy oba gwinty śruby i nakrętki mają dokładnie ten sam skok a ich odkształcenia są tego samego znaku i są równe, co do wartości. Najczęściej jednak śruba jest rozciągana, a następnie ściskana oraz nakrętka jest zwykle sztywniejsza od śruby. Skutkiem tych zjawisk pierwsze zwoje śruby w pobliżu powierzchni oporowej nakrętki są silnie przeciążone.
Nie znając prawdziwego rozkładu obciążenia posługujemy się uproszczonym rachunkiem przyjmując równomierny rozkład obciążenia, a obliczone naprężenia nominalne ograniczymy do wartości określonych dopuszczalnie.
Gwint może być narażony na zniszczenie powierzchni wskutek:
- nadmiernych nacisków powierzchniowych na współpracujących powierzchniach śruby i nakrętki,
- naprężeń gnących,
- naprężeń ścinających.
W śrubach obliczanych z warunku nacisków powierzchniowych wartości naprężeń gnących i ścinających są bardzo małe i dlatego obliczanie połączeń gwintowych przeprowadza się z warunku na naciski powierzchniowe.
Nacisk jednostkowy na powierzchni roboczej gwintu (Rys. 12) wynosi
![]()
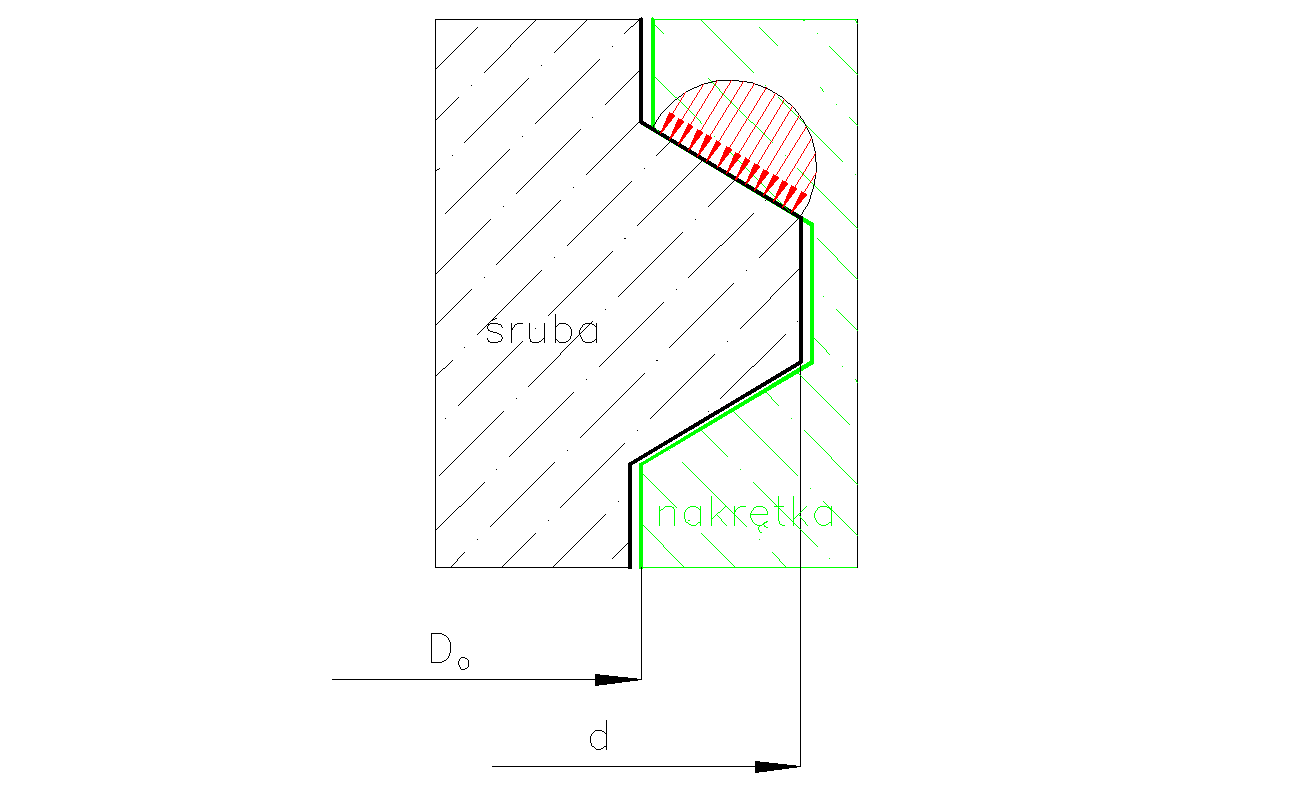
Rys. 12. Rozkład nacisków powierzchniowych
n - liczba czynnych zwojów połączenia (liczba stykających się zwojów śruby i nakrętki);
![]()
gdzie:
![]()
- siła normalna do powierzchni gwintu ![]()
;
![]()
- robocza powierzchnia gwintu ![]()
( F - pole rzutu powierzchni ![]()
na płaszczyznę prostopadłą do osi)
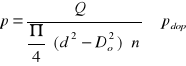
Ponieważ liczba czynnych zwojów n jest równa
![]()
gdzie:
![]()
- wysokość nakrętki,
![]()
- wielokrotność zwoju,
![]()
- skok gwintu.
Możemy wyznaczyć potrzebną wysokość nakrętki
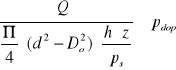
![]()
![]()
Nakrętka obliczona na nacisk zdolna jest przenieść większą siłę osiową niż rdzeń śruby na rozerwanie.
W przypadku normalnych łączników gwintowych tworzących połączenia spoczynkowe (śruby złączne) i wykonanych z tego samego materiału, co nakrętka wysokość nakrętki przyjmuje się ![]()
.
W przypadku gwintów rurowych wysokość nakrętki ![]()
; gdzie g - grubość ścianki rury.
Wysokość ![]()
nakrętki liczymy gdy:
- śruba i nakrętka wykonane są z różnych materiałów;
- połączenie jest ruchowe lub półruchowe;
- ze względów konstrukcyjnych trzeba zaprojektować nakrętkę o mniejszej od znormalizowanej wysokości.
Długość wkręcenia gwintu łącznika znormalizowanego tzw. czynnej długości gwintu ![]()
, w praktyce nie obliczamy. Najmniejsza czynna długość gwintu stalowego ![]()
, brązowego ![]()
, żeliwnego![]()
, a wykonanego ze stopu lekkiego ![]()
.
Obliczanie wytrzymałość rdzenia śruby
Obliczenia śruby i nakrętki uzależnione są od rodzaju i charakteru obciążenia śruby.
Przystępując do obliczeń wytrzymałościowych należy ustalić rodzaj i charakter obciążenia działającego na śrubę. Obciążenie śrub można sprowadzić do czterech najczęściej spotykanych przypadków:
-1.złącze samohamowne obciążone siłą osiową stałą albo zmienną bez wstępnego napięcia śruby,
-2.złącze samohamowne bez wstępnego napięcia obciążone siłą osiową i momentem skręcającym,
-3.złącze śrubowe obciążone siłą poprzeczną,
-4.śruby robocze.
Przypadek 1
Śruba skręcona swobodnie bez napięcia wstępnego, a następnie obciążona siłą osiową Q stałą lub zmienną (np. gwintowany koniec haka dźwigu).
Przekrój rdzenia śruby jest narażony na rozciąganie i musi być spełniony elementarny warunek wytrzymałościowy
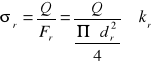
[MN/m2]
![]()
gdzie:
![]()
- siła rozciągająca śrubę w [MN],
![]()
- średnica rdzenia śruby w [m],
![]()
- dopuszczalne naprężenia na rozciąganie w [MN/m2].
dla obciążeń statycznych ![]()
(![]()
- granica plastyczności dla materiału śruby, ![]()
.
Dla obciążeń zmiennych tętniących 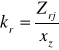
(![]()
- wytrzymałość zmęczeniowa przy jednostronnym rozciąganiu ![]()
, współczynnik ![]()
- dla obliczeń wstępnych.
Przypadek 2
Przekrój rdzenia śruby jest narażony na rozciąganie lub ściskanie siłą osiową ![]()
oraz na skręcanie momentem skręcającym ![]()
(np. nakrętka rzymska, podnośnik).
W tym przypadku naprężenia rozciągające (lub ściskające) wynoszą
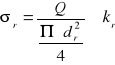
[MN/m2]
a naprężenia skręcające
![]()
gdzie:
![]()
a ![]()
moment tarcia na gwincie wywołany siłą obwodową ![]()
![]()
![]()
![]()
![]()
stąd
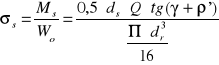
O wytężeniu materiału decyduje naprężenia zastępcze wg hipotezy Hubera
![]()
Stosunek ![]()
zwany współczynnikiem redukcyjnym wynosi:
- dla obciążeń statycznych ![]()
,
- dla obciążeń tętniących 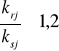
Dla śrub o gwincie metrycznym: ![]()
; ![]()
; ![]()
;
naprężenia skręcające wynoszą ![]()
;
naprężenia zastępcze ![]()
.
Wystarczy, więc obliczyć takie śruby jak gdyby były obciążone wyłącznie siłą osiową ![]()
na rozciąganie lub ściskanie.
Śruby ściskane należy ponadto sprawdzić na wyboczenie wg Eulera lub Tetmejera przyjmując promień bezwładności ![]()
.
Literatura S. Małuszyński „Podstawy Konstrukcji Maszyn i Urządzeń Pożarniczych” SGSP rozdz. 2.3. str. 50.
Przypadek 3
Śruba ma przenieść obciążenie poprzeczne ![]()
działające w płaszczyźnie styku elementów łączonych.
Jeżeli jest to śruba pasowana - mamy złącze kształtowe.
Opór pasowanego rdzenia śruby przeciw ścinaniu równoważy siłę poprzeczną ![]()
(Rys. 13).
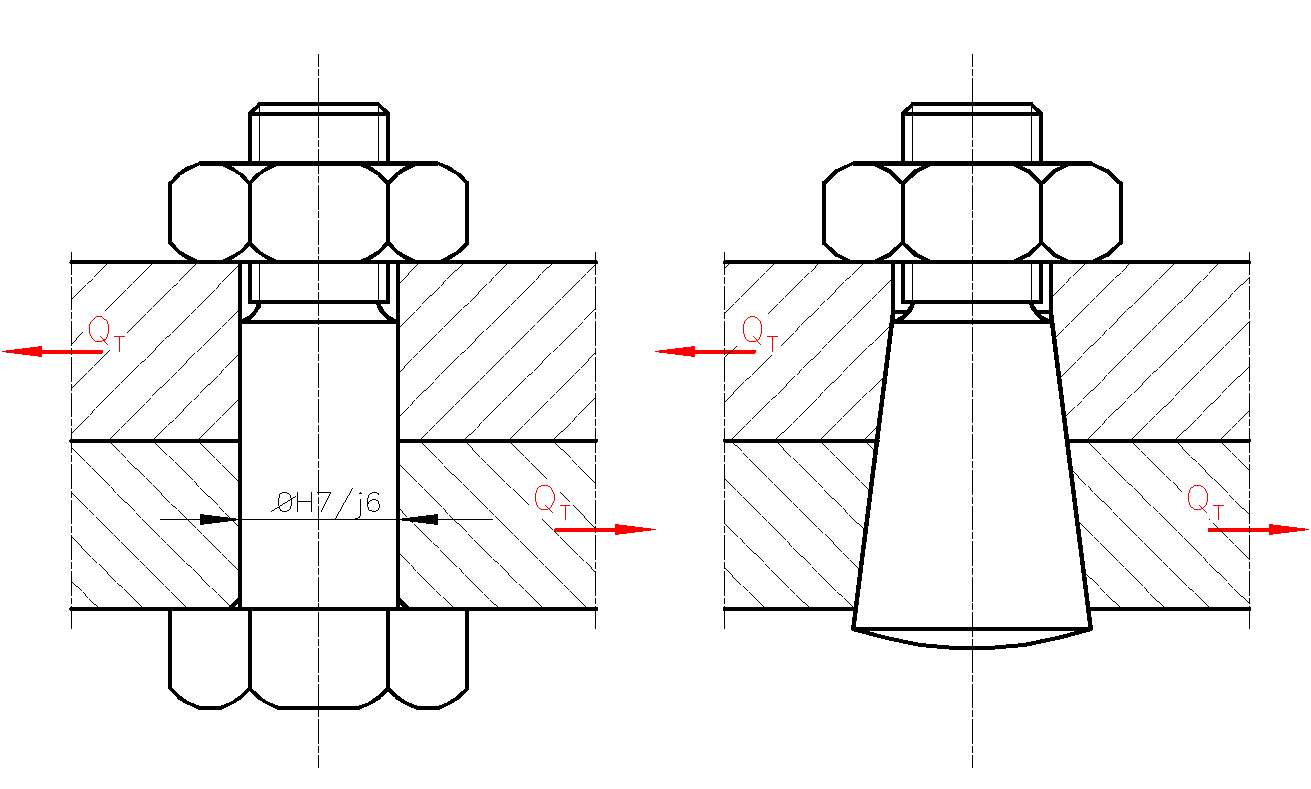
Rys. 13. Śruby pasowane
Nominalne naprężenia tnące w ścinanym przekroju śruby
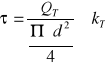
` [MN/m2]
gdzie:
![]()
- siła poprzeczna,
![]()
- średnica gwintu śrubowego,
![]()
- dopuszczalne naprężenia tnące - dla obciążeń statycznych ![]()
,
dla obciążeń wahadłowych ![]()
, dla pulsujących ![]()
.
Złącze może również ulec uszkodzeniu wskutek powstania trwałych odkształceń na ich bocznych ściankach po przekroczeniu granicznych nacisków powierzchniowych.
![]()
[MN/m2]
gdzie:
![]()
- grubość ścianki elementu obciążonego siłą ![]()
w [m],
![]()
- średnica otworu w miejscu pasowania śruby w [m],
![]()
- dopuszczalny nacisk powierzchniowy ![]()
.
Przypadek 4
Śruby robocze
Do śrub roboczych zalicza się śruby, które po obciążeniu siłą osiową obracane są względem nakrętki (np. gwintowe wrzeciona zaworów, śruby stosowane w podnośnikach śrubowych, śruby pociągowe w obrabiarkach).
Śruby robocze mają zwykle gwinty trapezowe o różnych kątach wzniosu.
Metodyka przeprowadzania obliczeń śrub roboczych
Wstępnie oblicza się przekrój śruby z warunku na rozerwanie i powiększa się go o 25%.
![]()
z tablicy gwintów trapezowych dobiera się śrubę o przekroju zbliżonym do obliczanego, przyjmując jednocześnie odpowiednią wartość kąta wzniosu ![]()
.
Dla taki dobranej śruby oblicza się naprężenia zastępcze i sprawdza warunek poprawnej konstrukcji wg zależności
![]()
[MN/m2]
gdzie
![]()
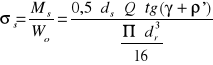
![]()
- średnia średnica gwintu,
![]()
- średnica rdzenia śruby,
![]()
współczynnik redukcyjny:
- dla obciążeń statycznych ![]()
,
- dla obciążeń tętniących ![]()
.
Obliczenia długich śrub ściskanych
Długie ściskane śruby oblicza się z uwzględnieniem wyboczenia. Teorią zjawiska wyboczenia zajmuje się nauka o wytrzymałości materiałów. Metodyka obliczeń w przypadku długich śrub ściskanych jest taka sama jak metodyka obliczeń słupów i prętów.
Rozpoczynamy od określenia smukłości pręta (śruby). Smukłość /![]()
/ nazywa się stosunek długości swobodnego wyboczenia /![]()
/ do ramienia bezwładności /![]()
/ (![]()
- promień bezwładności przekroju poprzecznego pręta).
![]()
długość swobodnego wyboczenia ![]()
zależy od sposobu mocowania pręta, ramię bezwładności ![]()
gdzie:
![]()
- moment bezwładności przekroju rdzenia śruby względem średnicy,
![]()
- przekrój rdzenia śruby,
tak więc smukłość
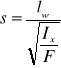
Rozróżnia się następujące przypadki ściskania prętów.
pręty nie ulegające wyboczeniu o smukłościach
![]()
w przypadkach śrub ściskanych o smułościach ![]()
obliczeń wyboczeniowych nie przeprowadza się, ograniczając się do obliczeń z warunku na ściskanie
![]()
gdzie:
![]()
- dopuszczalne naprężenia na ściskanie w [MN/m2].
pręty ulegające wyboczeniu trwałemu o smukłościach
![]()
większych od smukłości minimalnej a mniejszych od smukłości krytycznej dla danego materiału.
W tym przypadku naprężenia oblicza się z warunku na wyboczenia
![]()
gdzie:
![]()
- krytyczna wytrzymałość na wyboczenie określona ze wzoru Tetmajera
![]()
dla stali o module sprężystości ![]()
![]()
[MPa] ![]()
dla stali o module sprężystości ![]()
![]()
[MPa] ![]()
Po obliczeniu wytrzymałości na wyboczenie ![]()
wprowadza się współczynnik bezpieczeństwa
![]()
Wartość dopuszczalnego współczynnika bezpieczeństwa ![]()
przy obliczeniach wg Tetmajera
![]()
najczęściej ![]()
pręty ulegające wyboczeniu sprężystemu o smukłości /s/
![]()
większej od smukłości krytycznej dla danego materiału.
W tym przypadku wytrzymałość na wyboczenie określa się ze wzoru Eulera
![]()
dla stali o module sprężystości ![]()
![]()
dla stali o module sprężystości ![]()
![]()
Po obliczeniu wytrzymałości na wyboczenie sprawdza się współczynnik bezpieczeństwa ![]()
![]()
gdzie:
![]()
- dopuszczalny współczynnik bezpieczeństwa dla wytrzymałości na wyboczenie określonej ze wzoru Eulera
![]()
Parametrem decydującym o wyborze zależności, z której wyznaczone będzie naprężenie krytyczne /![]()
/ jest smukłość /![]()
/.
Smukłość /![]()
/ definiowana jest jako stosunek swobodnej długości wyboczenia /![]()
/ do promienia bezwładności przekroju /![]()
/:
![]()
Swobodna długość wyboczenia śruby zależy jedynie od sposobu jej zamocowania i wynosi:
![]()
[m]
gdzie:
![]()
- współczynnik zależny od sposobu zamocowania końców śruby;
![]()
- długość śruby w [m],
natomiast promień bezwładności jej przekroju:
![]()
gdzie:
![]()
- średnica rdzenia śruby w [m].
Po przekształceniu smukłość śruby określa zależność:
![]()
Po dobraniu znormalizowanych wymiarów gwintu trapezowego symetrycznego/ Tr d x ps / należy sprawdzić czy przyjęte na wstępie założenie, że wyboczenie będzie miało miejsce w obszarze odkształceń sprężystych, gdzie /λ> λkr/, jest prawdziwe.
W tym celu określa się rzeczywistą smukłość układu /λrz/:
![]()
gdzie:
d3 - znormalizowana średnica rdzenia śruby [m],
i porównuje ze smukłością krytyczną /λkr/ właściwą dla materiału, z którego wykonano śrubę.
Jeżeli okaże się, że smukłość rzeczywista /λrz/ jest równa lub większa od smukłości krytycznej /λkr/:
![]()
tzn, że wyboczenie zachodzi w obszarze wyboczenia sprężystego, obliczenia należy przeprowadzić wyznaczając średnicę rdzenia śruby /dr/ z zależności Eulera.
Wówczas do warunku wytrzymałościowego w postaci:
![]()
wprowadzamy krytyczne naprężenia ![]()
opisane zależnością Eulera:
![]()
[MPa]
gdzie:
![]()
i otrzymuje:
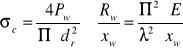
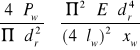
![]()
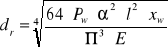
[m]
Połączenia śrubowe i gwintowe - wykład
-----------------------------------------------------------------------------------------------------------------
------------------------------------------------------------------------------------------------------------
Strona 26 z 27
Wyszukiwarka
Podobne podstrony:
PONTIAC GRAND PRIX 1988 2005
MERCEDES BENZ 300CE 1988
istorija russkoj mafii 1988 1994 bolshaja strelka
kpk, ART 564 KPK, 1988
Ballada o Januszku (1988) (TV), BALLADA O JANUSZKU
1988 (10)
JEEP WRANGLER 1988 2004
BMW 635CSi 1988
Karta Praw Podstawowych Unii Europejskiej rewizja 1988
MERCEDES BENZ 190E 1988
1988 frem (11)
BMW 750iL 1988
BUICK ELECTRA 1988 1990
MP 1988 025 0219 id 318266 Nieznany
MAZDA 626 1988
1988
1988
1988 frem (10)
1988 11 Żadło frontu N
1988 13 Kurs bojowy Bieszczady
więcej podobnych podstron