Dyfrakcja promieni rentgenowskich i jej zastosowanie.
Promieniowanie rentgenowskie jest to promieniowanie elektromagnetyczne o długości fali od ![]()
do![]()
, przy czym w badaniach strukturalnych stosuje się fale z zakresu ![]()
. Źródłem tych promieni są lampy rentgenowskie, izotopy promieniotwórcze, akceleratory cząstek mające ładunek elektryczny. Najczęściej jednak praktyczne zastosowanie ma lampa rentgenowska, która składa się z naczynia próżniowego i znajdujących się w nim elektrod: anody, katody i cylindra Wehnelta. Katodę stanowi drucik wolframowy nagrzewany do temperatury rzędu 2500K, który staje się źródłem swobodnych elektronów. Te elektrony po uformowaniu przez cylinder Wehnelta w postaci wiązki są przyspieszane polem elektrycznym panującym między katodą i anodą wytworzone poprzez przyłożone do nich dużej różnicy potencjałów. W wyniku tego przyspieszenia elektrony uzyskują dużą energie kinetyczną, którą tracą uderzając w anodę wywołując przy tym szereg niezależnych zjawisk, w których powstają widma promieniowania rentgenowskiego i w zależności od sposobu hamowania strumienia można je podzielić na widmo ciągłe charakterystyczne czyli liniowe.
Widmo ciągłe powstaje wtedy gdy hamowanie swobodnego elektronu na anodzie odbywa się jako szereg skokowych zmian jego energii przy kolejnych zderzeniach z atomami anody. Wiązka pędzących elektronów stanowi prąd elektryczny wytwarzający wokół siebie pole magnetyczne, które przy takich zderzeniach ulega zmianie dając początek falom elektromagnetycznym. Przy każdej zmianie energii ![]()
elektronu odpowiada emisja kwantu o energii ![]()
, spełniającej równość ![]()
. Całkowity bilans energetyczny możemy więc napisać w postaci
![]()
Wielkość energii poszczególnych kwantów ![]()
jest przypadkowa. Jeżeli elektron porusza się w kierunku anody z prędkością ![]()
, wówczas posiada energię kinetyczną ![]()
. Energię tę otrzymał wskutek przyspieszenia w polu elektrycznym. Pole to wykonało więc pracę równą ![]()
, gdzie ![]()
- jest napięciem między katodą i anodą a ![]()
- ładunek elektronu. Jeżeli cała energia kinetyczna elektronu zostanie w jednym zderzeniu przekształcona w kwant promieniowania rentgenowskiego to w tym przypadku ma on maksymalną częstotliwość lub też odpowiednio minimalną długość fali ![]()
, którą możemy wyznaczyć korzystając z zależności
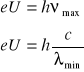
![]()
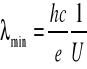
gdzie
![]()
stała Plancka, ![]()
częstotliwość drgań, ![]()
prędkość światła, ![]()
długość fali.
Promieniowanie liniowe zależy tylko od liczby emitującego je pierwiastka anody i stąd często nazywane jest promieniowaniem charakterystycznym. To widmo powstaje wtedy gdy jej atomu elektron powoduje przejście atomu w stan wzbudzony, który jest nietrwały i puste miejsce zostaje natychmiast zapełnione elektronem pochodzącym z dalszych powłok, a to związane jest z emisją kwantu o stosunkowo dużej energii określonej przez prawo Moseleya
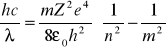
, gdzie ![]()
liczba porządkowa pierwiastka, ![]()
masa elektronu, ![]()
przenikalność elektryczna próżni.
A więc promieniowanie charakterystyczne emitowane jest w wyniku przeskoku elektronu z orbity ![]()
na orbitę o numerze ![]()
, przy czym zawsze ![]()
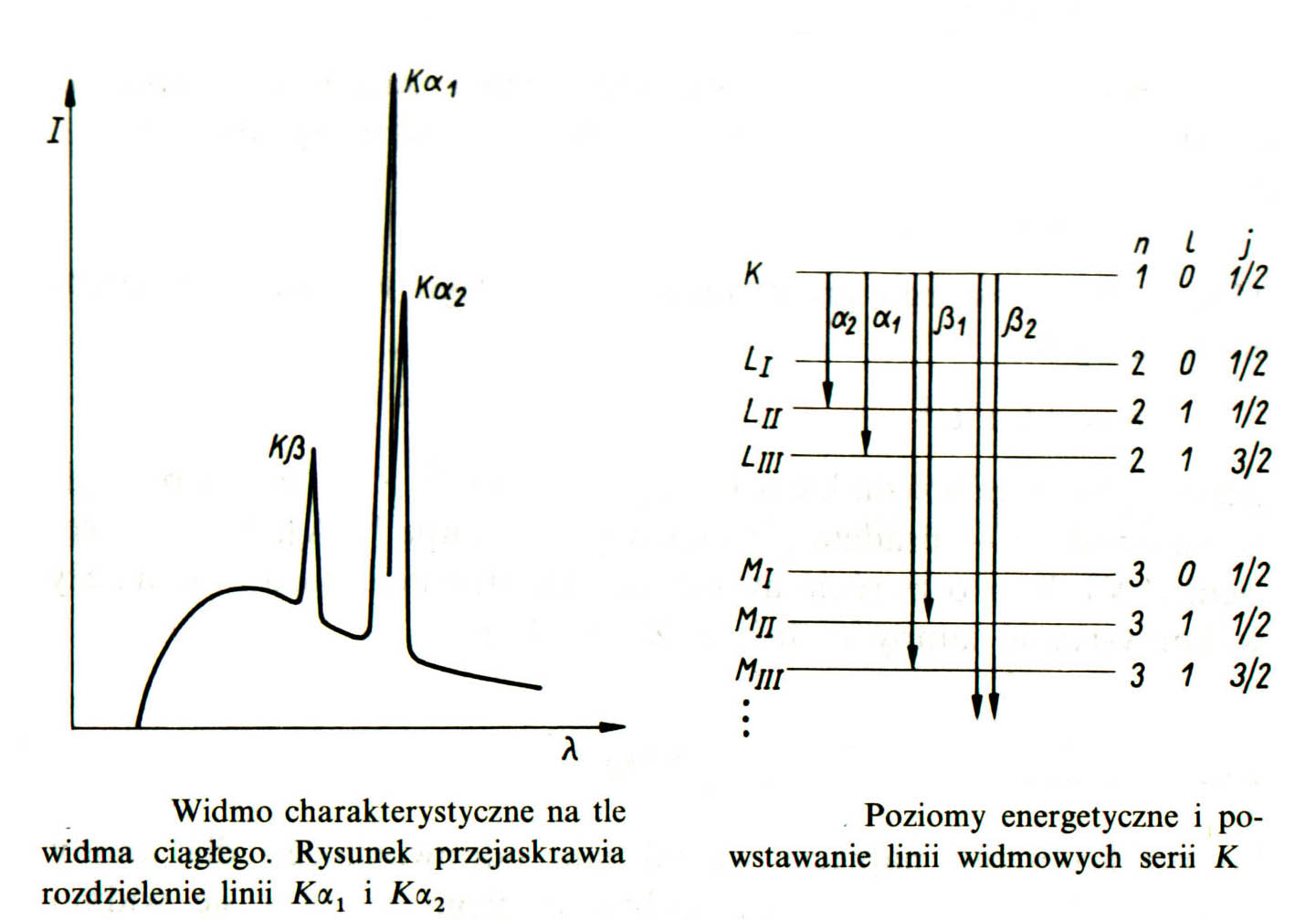
. W związku z tym długość fal tego promieniowania grupuje się w tzw. serie oznaczone dużymi kolejnymi literami alfabetu: K, L, M., N, itd. które określają na którą powłokę przechodzi elektron.
Widmo rentgenowskie składają się z dwóch widm nałożonych na siebie: widma ciągłego i liniowego, których natężenie zależne od długości fali przedstawia wykres:
W zjawisku Comptona wiązka promieni rentgenowskich o jednakowej długości fali przepuszczona zostaje przez materiał posiadający swobodne elektrony np. blok grafitowy. W wyniku czego promienie rozpraszane posiadają dwa maksymalne natężenie dla dwóch różnych długości fali. Jedno maksymalne natężenie jest dla fali padającej na ten blok, a drugie powstaje, dlatego że fotony tej wiązki zderzają się z luźno związanymi elektronami grafitu przekazując im część swojej energii, która wiąże się z zmianą długości fali. W procesie zderzenia się fotonu z elektronem zachowana jest nie tylko energia ale i pęd. Korzystając z tych zasad można wyznaczyć o ile zwiększy się długość fali rozproszonej.
![]()
,
![]()
częstotliwość fotonu przed i po zderzeniu, ![]()
masa spoczynkowa i relatywistyczna elektronu.
![]()
,
![]()
pęd fotonu przed i po kolizji.,![]()
prędkość elektronu uzyskana po zderzeniu z fotonem.
Korzystając z twierdzenia cosinusów można zapisać
![]()
.
Podstawiając za pęd fotonu zależność ![]()
uzyskujemy
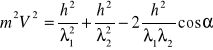
.
Równanie na zachowanie energii przekształcamy w następujący sposób
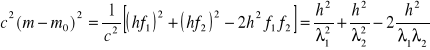
.
Odejmujemy od siebie dwa powyższe równania
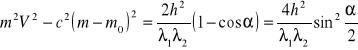
.
Za masę relatywistyczną podstawiamy
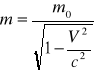
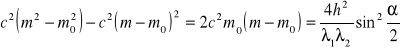
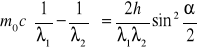
Na przesunięcie comptonowskie otrzymujemy wzór
![]()
.
Sieć przestrzenna, parametry sieci.
Kryształy są jednorodnymi anizotropowymi ciałami, które składają się
z atomów, jonów lub cząsteczek rozmieszczonych w prawidłowy sposób. Zastępując je (elementy strukturalne) ich geometryczna reprezentacją - punktami (węzłami) otrzymujemy sieć przestrzenną. W sieci tej możemy wyróżnić płaszczyzny i proste. Wszystkie równoległe płaszczyzny i wszystkie równoległe proste są sobie równoważne. Wobec tego, jeżeli w sieci przestrzennej określimy układ osi współrzędnych, to bezwzględne położenie płaszczyzny lub prostej nie ma znaczenia, istotne jest nachylenie płaszczyzny lub prostej względem osi układu.
Płaszczyznę określić można za pomocą pewnej zależności zdefiniowanej w taki oto sposób: stosunki odcinków, jakie dwie ściany odcinają na osiach współrzędnych liczby, wyrażają całkowite. się przez niewielkie Jeżeli jedną ze ścian przyjąć za jednostkową tj. ściana ta odcina na osiach układu odcinki 1, 1, 1 w jednostkach osiowych a, b, c, to można napisać:
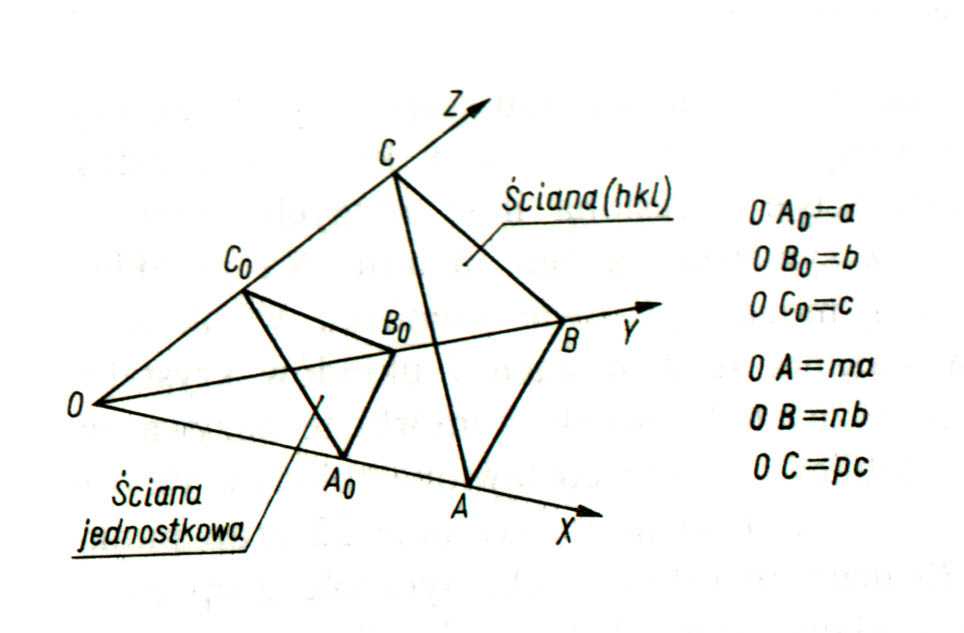
![]()
Trzy liczby całkowite h, k, l wzięte w nawias okrągły z opuszczeniem przecinków — (hkl) nazywają się wskaźnikami Millera. Inaczej można określić wskaźniki Millera, jako liczby wskazujące na ile części dana ściana (najbliższa początkowi układu) dzieli podstawowe periody a, b, c na osiach układu współrzędnych. Ten sposób określania wskaźników Millera jest przedstawiony na rysunku poniżej;
Prostą sieciową wyznaczają współrzędne dwóch węzłów. Przyjmując początek układu współrzędnych w jednym z węzłów, współrzędne drugiego węzła określają prostą sieciową — jej orientację. Symbolem prostej są liczby całkowite u, v, w wzięte w nawias kwadratowy [uvw].
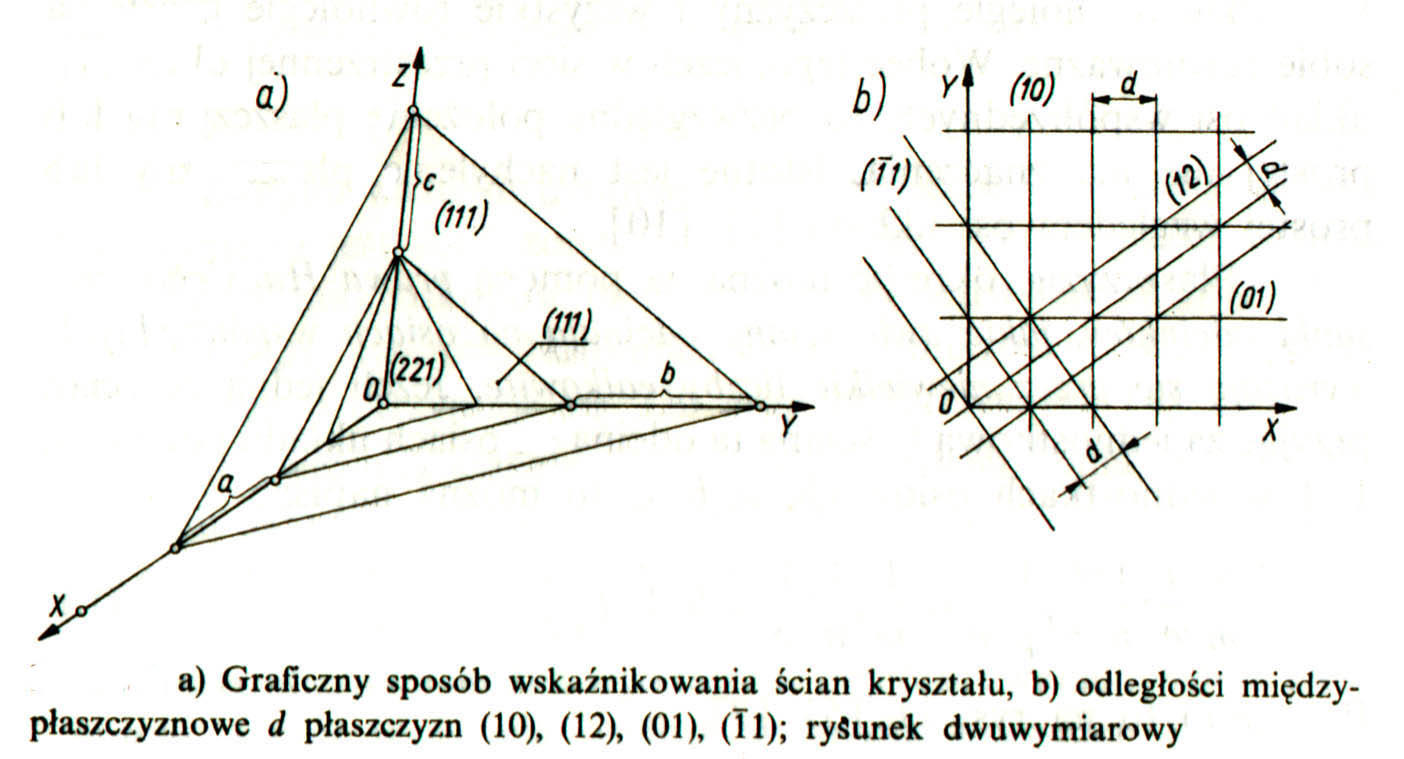
Wskaźnikowanie linii dyfrakcyjnych dla układów regularnych polega na wyznaczeniu dla każdej rozproszonej linii wskaźników h, k, l. Z prawa Bragga odległość międzypłaszczyznowa wynosi ![]()
, którą podstawiamy do równania ![]()
otrzymując ![]()
. Z tej równości uzyskujemy: ![]()
. Określając wskaźniki dla danej linii dyfrakcyjnej musimy określić kąt ![]()
pod jakim ugina się pojedyncza linia a następnie trzeba założyć z jakiego typu kryształem mamy do czynienia aby określić wskaźniki dla pierwszej linii. Następnie biorąc stosunek wartości ![]()
dla dwóch linii: pierwszej i „i-tej” mamy; 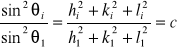
.Uzyskany wynik z pomiaru![]()
rozkładamy na trzy liczby całkowite hi, ki, li, które spełniają warunek ![]()
.
Max fon Laue dokonał analizy promieni rentgenowskich opisał to zjawisko matematycznie formułując równania, które są obecnie nazywane równaniami Lauego. Opisują one zjawisko dyfrakcji promieni na trójwymiarowej sieci przestrzennej a w szczególności na prostej i płaszczyźnie sieciowej. Przy opisie tych zjawisk Laue dokonał pewnych założeń: Kryształ ma prawidłową budowę bez jakichkolwiek zniekształceń, którego atomy są nieruchome. Następnie wiązka padająca na ten kryształ jest równoległa i nie jest przez niego pochłaniana.
Wiązka ta o długości fali λ pad pod kątem α0 na prostą sieciową o okresie identyczności a i zostaje ugięta pod kątem α. Rozpatrujemy promienie 1 i 2, których czoło wyznacza prosta PA. Na odcinkach AR i PB fale te mają do przybycia niejednakowe drogi. Różnica tych odcinków stanowi różnicę dróg ΔS rozważnych promieni:
![]()
![]()
.
Ugięte promienie mogą się wzajemnie wzmacniać jeżeli powyższa różnica dróg jest równa całkowitej wielokrotności długości fali, czyli gdy:
![]()
![]()
,
gdzie: h - liczba całkowita, λ - długość fali.
Mamy więc:
![]()
.
Uwzględniając, że:
![]()
otrzymujemy:
![]()
.
Jest to tzw. równanie Lauego określające kierunek rozchodzenia się wzmocnionego promienia interferencyjnego w przypadku ugięcia promieni na prostej sieciowej. W wszystkich innych kierunkach nie spełniających powyższego równania przy dostatecznej ilości węzłów na prostej sieciowej promienie wzajemnie się wygaszają. Gdy rozpatrzymy trzy proste sieciowe wzajemnie do siebie prostopadłe, której okres identyczności dla każdej wynosi kolejno: a, b, c, to wzmocniony promień interferencyjny powstanie wtedy, gdy jednocześnie będą spełnione trzy równania Lauego:
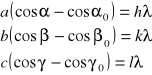
Równania Lauego i równanie Bragga opisują to samo zjawisko fizyczne wobec tego są sobie równoważne, co najłatwiej można wykazać dla układów prostokątnych. Rozpatrując regularną sieć przestrzenną (a=b=c), na którą padają promienie rentgenowskie równoległe do jednych z osi np. do osi ![]()
.
Promienie te tworzą z osiami krystalograficznymi następujące kąty
z osią x - kąt α0 = 90º
z osią y - kąt β0 =90º

z osią z - kąt γ0= 0º
Równania Lauego:
![]()
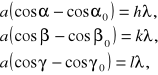
przyjmują więc w rozważanym przypadku następującą postać:
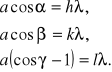
Ugięty promień R' tworzy z kierunkiem promienia padającego R:
-kąt γ - według teorii Lauego,
-kąt 2θ- według teorii Bragga.
Mamy więc: γ=2θ.
Podnosząc powyższe równania do kwadratu i dodając do siebie otrzymujemy
![]()
.
Dla układów prostokątnych:
![]()
,
![]()
.
Wyrażenie stojące po lewej stronie równości można przekształcić w następujący sposób:
![]()
,
![]()
Uwzględniając formę kwadratową dla rozważanego układu ![]()
![]()
i pierwiastkując obustronnie ![]()
otrzymujemy prawo Bragga
![]()
.
Opisuje ono podobnie jak równania Lauego zjawiska dyfrakcji promieni rentgenowskich na płaszczyznach sieciowych o wzajemnych odległościach równych dhkl . Z uwzględnieniem rzędów linii dyfrakcyjnych prawo Bragga ma postać:
![]()
, gdzie: n - rząd ugięcia, θ - kąt między promieniem padającym a płaszczyzną sieciową.
Metoda Debye'a-Schelerrera-Hulla jest podstawową metodą badania substancji polikrystalicznych, w której stosuje się filtrowaną wiązkę promieni rentgenowskich padającą na odpowiednio uformowany preparat polikrystaliczny. Te preparat wykonuje się w taki sposób aby zawierały duże ilości chaotycznie ułożonych krystalitów. Najczęściej napełnia się proszkiem cienkościenne kapilary szklane lub nakleja się proszek na szklaną nić. Płaszczyzny sieciowe o ustalonej odległości międzypłaszczyznowej są więc w preparacie ułożone również chaotycznie i uginają promienie rentgenowskie w różnych kierunkach, lecz zawsze pod tymi samymi kątami 2θ w stosunku do padających promieni. W wyniku tego promienie ugięte na tych samych płaszczyznach (hkl) różnych krystalitów tworzą powierzchnie stożkową o kącie rozwarcia 4θ. Osią wszystkich stożków dyfrakcyjnych jest kierunek wyznaczony przez oś wiązki pierwotnej. Kamerę Debye'a-Scherrera-Hulla stanowi metalowy wewnątrz wydrążony walec, na którego bocznej powierzchni o promieniu R umieszcza się film rentgenowski, na którym uzyskuje się układ linii dyfrakcyjnych symetryczny względem punktu na którego padałaby wiązka gdyby nie było preparatu. Linie rozmieszczone są w kolejności wzrostu kątów dyfrakcji od środka filmu ( θ=0º) do jego końców (θ=90º). Odległość 2L między dwoma dowolnymi symetrycznymi liniami dyfrakcyjnymi wynosi:
w mierze łukowej:
2L=4θ*R,
gdzie: L- odległość danej linii dyfrakcyjnej od środka kliszy.
w mierze kątowej:
![]()
Z tych zależności znając L i R można wyznaczyć kąt θ, z który jest potrzebny do określenia parametrów sieci i wskaźników h, k, l.
Wyznaczanie stałej Plancka
Tą stałą możemy wyznaczyć korzystając z wzoru na granicę krótkofalową
![]()
,
![]()
![]()
![]()
.
Podstawiając za λmin z równania Bragga dla pierwszego rzędu linii dyfrakcyjnych ![]()
, uzyskujemy wyrażenie
![]()
![]()
.
Znajdujemy zależność jak zmienia się θ dla krótkofalowej granicy od napięci U
anody czyli 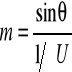
wyznaczmy stałą Planca.
1
9
P1![]()
![]()
P2
α
mV
β
y
α
x
z
β0
α0
R'
R
γ
Paweł Zygmunt
IV Fizyka z inf.
R
α0
α
2
1
A
P
BBB
Wyszukiwarka
Podobne podstrony:
pierwsza strona sprawozdania, fff, dużo
FIZYKA 47, fff, dużo
76bmoje, fff, dużo
Indukcyjność cewki, fff, dużo
Lab fiz 01, fff, dużo
Pomiar predkosci dzieku w powietrzu, fff, dużo
FIZ43'' 222222222, fff, dużo
Wyznaczanie temperatury Curie dla ferrytow, fff, dużo
fotometr Bunsena 75, fff, dużo
Lab fiz 05, fff, dużo
Lab fiz 24, fff, dużo
Lab fiz 04, fff, dużo
przenikalność, fff, dużo
Stala siatka dyfrakcji2, fff, dużo
wahadlo maxela 4422, fff, dużo
Fiz24 teoria, fff, dużo
więcej podobnych podstron