Obliczenia hydrologiczne
Przepływ absolutnie średni
Qs= 0.03171⋅Cs⋅P⋅A
Qs= 0.03171⋅0.4⋅0.656⋅1.21=0.0101 [m3⋅s-1]
gdzie:
A - powierzchnia zlewni - 1,21 km2
P - średni opad roczny - 656 mm = 0,656 m
Cs - współczynnik charakteryzujący rzeźbę terenu, odczytany z podręcznika: Cz.Zakaszewski „ Melioracje rolne” t.I. str.45
Przepływ absolutnie najniższy
Qo=0.2⋅υ⋅Qs
Qo=0.2⋅0.4125⋅0.0101=0.0008 [m3⋅s-1]
gdzie:
υ - współczynnik charakteryzujący rzeźbę terenu i przepuszczalność gleby, odczytany z podręcznika: Cz. Zakaszewski „ Melioracje rolne”
Qs - obliczony jak wyżej.
Przepływ najniższy doroczny
Q1=0.4⋅υ⋅Qs
Qs=0.4⋅0.4125⋅0.0101=0.0017 [m3⋅s-1]
gdzie:
υ - współczynnik charakteryzujący rzeźbę terenu i przepuszczalność gleby, odczytany z podręcznika: Cz. Zakaszewski „ Melioracje rolne”
Qs - obliczony jak wyżej.
Przepływ średni normalny
Q2=0.7⋅υ⋅Qs
Q2=0.7⋅0.4125⋅0.0101=0.0098 [m3⋅s-1]
gdzie:
υ - współczynnik charakteryzujący rzeźbę terenu i przepuszczalność gleby, odczytany z podręcznika: Cz. Zakaszewski „ Melioracje rolne”
Qs - obliczony jak wyżej.
Przepływ najwyższy tzw. katastrofalny
Q4=CW⋅m⋅P⋅A
Q4=0.155⋅24.937⋅0.656⋅1.21=3.0681 [m3⋅s-1]
gdzie:
Cw - współczynnik charakteryzujący rzeźbę terenu i przepuszczalności gleby, w tym obliczeniu przyjmowany na podstawie tzw. katalogu gruntu z podręcznika Cz. Zakaszewskiego „Melioracje rolne” t.I. str.45
m - współczynnik charakteryzujący wielkość powierzchni zlewni, odczytany z podręcznika Cz. Zakaszewski „ Melioracje rolne” t.I. str.48
P - średni opad roczny [m]
A - powierzchnia zlewni [km2]
Obliczenia wykonał: Bogusław Paśko
Przepływ doroczny wielki
Q3L=0.4⋅Q4
Q3L=0.4⋅3.06=1.2240 [m3⋅s-1]
Obliczenie przepływu maksymalnego wzorem Leovego.
Qmax(l, z) = Q3(l, z) = k1⋅k2⋅k3⋅k4⋅P(l, z)⋅A [m3⋅s-1]
gdzie:
k - współczynniki zależne od parametrów lokalnych zlewni:
k1L = 2,75 - dla wód letnich
k2 = 0,44
k3 = 0,99
k4 = 1
k1, k2, k3, k4 - współczynniki odczytane z podręcznika :
E. Czetwertyński „Hydrologia” str. 351 - 352
Pl - opad letni [m]
A - powierzchnia zlewni [km2]
opad letni - Pl = 0,17⋅P = 0,17⋅ 0,656 = 0,164 [m]
Q3L = 2,75⋅0,44⋅0,99⋅1⋅0,122⋅1.21 =0,1768 [m3⋅s-1]
Obliczenia wykonał: Bogusław Paśko
Obliczenia hydrologiczne rowu A
Rodzaj użytków - grunty orne, trwałe użytki zielone
Przepływ miarodajny - 1,22 m3⋅ s-1
Nachylenie skarp - 1 : 1.5
Projektowana głębokość - 1.30 m
Zakładam t - napełnienie rowu wodą Q3L
t = h - s [m]
gdzie:
s - rezerwa zależna do rodzaju użytków
t = h - s = 1,30 - 0,30 = 1,0 m
Obliczenie pola powierzchni przekroju poprzecznego
![]()
![]()
Obliczenie obwodu zwilżonego
![]()
![]()
![]()
Obliczenie promienia hydraulicznego
![]()
![]()
![]()
Obliczenie współczynnika prędkości
wzorem Bazina
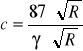
gdzie:
γ , - współczynnik szorstkości koryta rowu
dla dobrze utrzymanego koryta γ - 1.2
Obliczenia wykonał: Bogusław Paśko
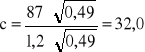
Obliczenie prędkości przepływu wody w rowie
![]()
Imin,=4 ‰
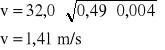
obliczenie przepływu rzeczywistego ( Qobl.)
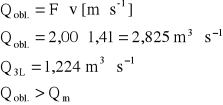
Obliczenia dla doboru odpowiedniego typu ubezpieczenia koryta rowu.
I. Wartości prędkości maksymalnych dla określonych rodzajów ubezpieczeń:
1. Darniowanie na płask
v = 1.0 m⋅s-1
2. Płotek , darniowanie kożuchowe, kiszka faszynowa
v = 1.25 m⋅s-1
3. Płotek podwójny bardzo staranne darniowanie, płytki chodnikowe
v = 1.5 m⋅s-1
4. Bruk z kamienia uszczelniony mchem, prefabrykowane płytki korytowe
v = 2.5 m⋅s-1
5. Bruk podwójny, płytki korytowe
v = 3.5 m⋅s-1
6. Mur z kamienia uszczelniony cementem
v = 4.5 m⋅s-1
Obliczenia wykonał: Bogusław Paśko
II. Obliczenie wartości spadku granicznego dla maksymalnej wartości prędkości
przy danym typie ubezpieczenia:
a) płotek podwójny bardzo staranne darniowanie, płytki chodnikowe.
Obliczenia rozpoczynam od wstawienia vmax. dla najsłabszego ubezpieczenia.
![]()
po przekształceniu otrzymuję:
![]()
![]()
![]()
Mając wcześniej ustalone wielkości b i n obliczam t z równania kwadratowego:
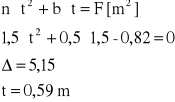
wielkości napełnienia t dla danego rodzaju ubezpieczenia przy prędkości wody vmax. a następnie wielkości obwodu zwilżonego O:
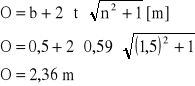
obliczam również wielkości c i R
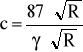
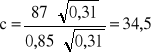
![]()
![]()
![]()
Obliczam spadek graniczny dla ubezpieczenia płotek podwójny bardzo staranne darniowanie,
płytki chodnikowe.
![]()
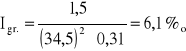
Obliczenia wykonał: Bogusław Paśko
b) bruk z kamienia uszczelniony mchem, prefabrykowane płytki korytowe
Obliczenia rozpoczynam od wstawienia vmax. dla najsłabszego ubezpieczenia.
![]()
po przekształceniu otrzymuję:
![]()
![]()
![]()
Mając wcześniej ustalone wielkości b i n obliczam t z równania kwadratowego
Mając wcześniej ustalone wielkości b i n obliczam t z równania kwadratowego:
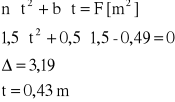
wielkości napełnienia t dla danego rodzaju ubezpieczenia przy prędkości wody vmax. a następnie wielkości obwodu zwilżonego O:
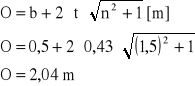
obliczam również wielkości c i R
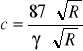
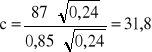
![]()
![]()
![]()
Obliczam spadek graniczny dla ubezpieczenia płotek podwójny bardzo staranne darniowanie,
płytki chodnikowe.
![]()
Obliczenia wykonał: Bogusław Paśko
c) bruk podwójny, płytki korytowe
Obliczenia rozpoczynam od wstawienia vmax. dla najsłabszego ubezpieczenia.
![]()
po przekształceniu otrzymuję:
![]()
![]()
![]()
Mając wcześniej ustalone wielkości b i n obliczam t z równania kwadratowego
Mając wcześniej ustalone wielkości b i n obliczam t z równania kwadratowego:
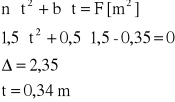
wielkości napełnienia t dla danego rodzaju ubezpieczenia przy prędkości wody vmax. a następnie wielkości obwodu zwilżonego O:
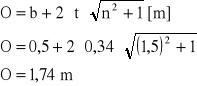
obliczam również wielkości c i R
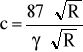
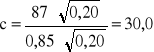
![]()
![]()
![]()
Obliczam spadek graniczny dla ubezpieczenia płotek podwójny bardzo staranne darniowanie,
płytki chodnikowe.
![]()
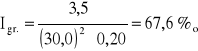
Obliczenia wykonał: Bogusław Paśko
Współczynnik szorstkości γ do wzoru Bazina
Współczynnik szorstkości γ może przyjmować następujące wartości
(C. Zakaszewski , Melioracje rolne, Odwodnienia t 1. PWR i L 1964 tab. 25)
1.Bardzo gładkie ściany (deski heblowane, gładka wyprawa cementowa) - 0.06
2.Gładkie ściany (deski nie heblowane, mur z ciosów lub cegły, mury betonowe i
żeliwne, bardzo dobre ściany bet. itp.) - 0.16
3.Nie gładkie ściany (dobry mur z kamienia łamanego) z betonu - 0.46
4. Mniej staranny mur z kamienia łamanego, bardzo niedokładne obetonowane skały,
bruk kamienny (kocie łby) ścianki ziemne w zwartych gruntach dobrze utrzymane,
ściany gładko kute w skale - 0.85
5. Koryta ziemne w zwykłym stanie koryta brukowane lecz nieco zarośnięte - 1.30
6. Koryta ziemne źle utrzymane, zarośnięte wodorostami, o dnie kamienistym lub z
otoczakami itp. - 1.75
Współczynnik szorstkości m do wzoru Kuttera
Współczynnik szorstkości m może przyjmować następujące wartości
(C. Zakaszewski , Melioracje rolne, Odwodnienia t 1. PWR i L 1964 tab. 26)
1. Ściany cementowe, czyste gładkie - 0.12
2. Ściany z desek drewnianych, heblowanych i dobrze dopasowanych - 0.15
3. Ściany z desek drewnianych dopasowanych, przewody stalowe i żelazne nowe oraz
żelbetonowe - 0.20
4. Czyste kanały kamionkowe, wodociągowe przewody żeliwne po dłuższym
użytkowaniu ściany z desek ni heblowanych - 0.25
5. Ściany staranie murowane z cegły - 0.27
6. Ściany z bali drewnianych i zwykłego muru z cegły - 0.35
7. Ściany z kamienia ciosanego - 0.45
8. Ściany ze starego muru wykonany i utrzymany - 1.50
9. Kanał ziemny zarośnięty trawą - 2.00
10. Kanał ziemny zaniedbany, zarośnięty trawą, o dnie zamulonym lub zarzucony
głazami - 2.50
Obliczenia wykonał: Bogusław Paśko
Obliczenie objętości robót ziemnych
rów „A”
Stacja |
Odległość między stacjami |
Przekrój projektowany |
Objętość |
Objętość narastająca |
|||
|
|
głębokość |
szerokość dna w [m] i nach. skarp |
powierzchnia |
|
|
|
|
|
|
|
na stacji |
średnia |
|
|
|
[m] |
[m] |
|
[m2] |
[m2] |
[m3] |
[m3] |
0+00 |
44
|
1,30 |
b = o,50 m nachylenie 1 : 1,5 |
3,19 |
3,47
|
152,46
|
0,00 |
0+44
|
|
1,42
|
|
3,74
|
|
|
152,46
|
|
30
|
|
|
|
3,47
|
103,95
|
|
0+74
|
|
1,30
|
|
3,19
|
|
|
256,41 |
|
32
|
|
|
|
3,66
|
117,12
|
|
1+06
|
|
1,50
|
|
4,13
|
|
|
373,53
|
|
18
|
|
|
|
3,66
|
65,88
|
|
1+24
|
|
1,30
|
|
3,19
|
|
|
439,41
|
|
26
|
|
|
|
3,19
|
82,94
|
|
1+50
|
|
1,30
|
|
3,19
|
|
|
522,35
|
|
46
|
|
|
|
3,19
|
146,74
|
|
1+96
|
|
1,30
|
|
3,19
|
|
|
669,09
|
|
20
|
|
|
|
3,19
|
63,80
|
|
2+16
|
|
1,30
|
|
3,19
|
|
|
732,89
|
|
22
|
|
|
|
3,28
|
72,05
|
|
2+38
|
|
1,34
|
|
3,36
|
|
|
804,94
|
|
24
|
|
|
|
3,28
|
78,60
|
|
2+62
|
|
1,30
|
|
3,19
|
|
|
883,54
|
|
32
|
|
|
|
3,19
|
102,08
|
|
2+94
|
|
1,30
|
|
3,19
|
|
|
985,62
|
|
24
|
|
|
|
3,19
|
76,56
|
|
3+18
|
|
1,30
|
|
3,19
|
|
|
1062,18
|
|
22
|
|
|
|
3,37
|
74,14
|
|
3+40
|
|
1,38
|
|
3,55
|
|
|
1136,32
|
|
22
|
|
|
|
3,37
|
74,14
|
|
3+66
|
|
1,30
|
|
3,19
|
|
|
1210,46
|
|
26
|
|
|
|
3,19
|
82,94
|
|
3+80
|
|
1,30
|
|
3,19
|
|
|
1293,40
|
|
14
|
|
|
|
3,19
|
44,66
|
|
4+06
|
|
1,30
|
|
3,19
|
|
|
1338,06
|
|
44
|
|
|
|
3,19
|
140,36
|
|
4+50
|
|
1,30
|
|
3,19
|
|
|
1478,42
|
|
18
|
|
|
|
3,19
|
57,42
|
|
4+68
|
|
1,30
|
|
3,19
|
|
|
1535,84
|
|
32
|
|
|
|
3,56
|
113,92
|
|
5+00
|
|
1,46
|
|
3,93
|
|
|
1649,76
|
|
12 |
|
|
|
3,56 |
42,72 |
|
5+12 |
|
|
|
3,19 |
|
|
1692,48 |
|
|
|
|
|
|
|
|
Obliczenia wykonał: Bogusław Paśko
Obliczenie rozstawy drenowania
Obliczenie rozstawy drenowania rozpoczynam od odczytania i zsumowania zawartości części spławialnych i 1/3 części pyłu drobnego. Dla poszczególnych warstw gruntu wynoszą one kolejno: warstwa I - 39 %, warstwa II - 45%, warstwa III - 60 %.
Następnie z wykresu do określenia rozstawy drenów na glebach słabo przepuszczalnych
(k < 0,2 m⋅d-1) oraz na glebach okresowo nadmiernie uwilgotnionych odczytuję rozstawę drenowania dla poszczególnych warstw w zależności od sumy procentowej zawartości części spławialnych ( < 0,02 mm) + 1/3 procentowej zawartości pyłu drobnego (0,02 - 0,05 mm).
I warstwa l = 15,0 [m] ; II warstwa l = 13,5 [m] ; III warstwa l = 11,1 [m].
Uwzględniając poprawkę ze względu na zawartość Fe2O3 , oraz poprawkę ze względu na zawartość CaCO3 (poprawki do rozstawy sączków określonej na podstawie składu mechanicznego wg wytycznych z 1978 r. - tab. 5.51. dr hab. P. Prochal „Podstawy melioracji rolnych” t.1 PWR i L Warszawa 1986 r.) przyjmuję rozstawy drenowania
l warstwa L= 16,5 [m] ; II warstwa L = 14,2 [m] ; III warstwa L = 11,1 [m].
Przyjęta głębokość drenowania 0,90 [m]
Następnie rozstawę drenowania dla całego profilu obliczam na podstawie średniej ważonej:
![]()
[m]
gdzie:
Li - rozstawa drenowania dla poszczególnej warstwy [m] ( L1= 16,5;L2 = 14,2; L3 = 11,1)
hi - miąższość poszczególnych warstw [m] ( h1 = 0,4; h2 = 0,4; h3 = 0,1)
zi - głębokość środka warstwy od powierzchni terenu [m] ( z1 = 0,2; z2 = 0,6; z3 = 0,9)
![]()
[m]
Średnio warzona rozstawa drenowania dla całego profilu wyniosła L = 14,0 [m]
Uwzględniając poprawki ze względu, na opad i ze względu na spadek terenu (prawki do rozstawy sączków określonej na podstawie składu mechanicznego wg wytycznych z 1978 r.
- tab. 5.51. dr hab. P. Prochal „Podstawy melioracji rolnych” t.1 PWR i L Warszawa 1986 r.) rozstawa średnia poprawiona wyniosła L = 13,4 [m]
Przyjmuję rozstawę drenowania L = 13 [m]
1 |
2 |
3 |
Numer sądy |
0,4 |
0,4 |
0,1 |
Miąższość warstwy hn [m] |
0,2 |
0,6 |
0,9 |
Głębokość zalegającej warstwy Zn [m] |
36 |
41 |
55 |
Zawartość części spławialnych % |
9 |
12 |
15 |
Zawartość pyłu drobnego % |
43,7 |
48,0 |
42,0 |
Wskaźnik zwięzłości gleby Wn % |
|
13,5 |
11,1 |
Rozstawa odczytana z nomogramu [m] |
|
3,5 |
5,5 |
Zawartość Fe2O3 % |
9,0 |
4,5 |
6,5 |
Zawartość CaCO3 % |
16,5 |
14,2 |
11,1 |
Rozstawa poprawiona [m] |
|
Rozstawa średnia ważona [m] |
||
|
Opad [mm] |
||
32 |
Średni spadek terenu % |
||
13,4 |
Rozstawa średnia poprawiona [m] |
||
13 |
Rozstawa przyjęta |
||
Obliczenia wykonał: Bogusław Paśko
Obliczenie przepustu.
Schematyczny przekrój podłużny przepustu drogowego.
Obliczenie przepustu rurowego prowadzącego wodę całym przekrojem obliczam wg wzoru Weissbacha.
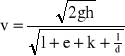
gdzie:
v - prędkość przepływu [m⋅s-1]
g - przyśpieszenie ziemskie [m/s2]
h - wysokość ciśnienia w m. Jest to wysokość zużyta przy przepływie wody przez przewód. Jeżeli wypływ jest wolny jest to wysokość równa odległości górnego zwierciadła wody od środka wylotu. Jeżeli wylot jest zatopiony, to jest równy różnicy poziomów wody górnej i dolnej. [m]
e - współczynnik dławienia
k - współczynnik chropowatości ( dla rur betonowych k = 0,02 )
l - długość przepustu [m]
d - średnica przepustu [m]
Obliczenie przepustu sprowadza się do doboru średnicy rury, która przeprowadzi przepływ doroczny wielki (Q3l).
Dane:
Q3l = Qm = 1,224 [m3⋅s-1]
l = 4,0 [m]
vdop = 2,0 [m⋅s-1]
Szerokość przepustu nie może być mniejsza niż szerokość dna rowu d>b
Obliczenie średnicy przepustu:
![]()
[m]
![]()
Fobl = 0,612 [m2]
![]()
dobl = 0,88 [m] Obliczenia wykonał: Bogusław Paśko
Mimo,że dobl<dkat=1,0m,warunek ostatni sprawdzający t + hstr < h - s nie jest spełniony n przyjmuję dwie rury.
![]()
dobl=![]()
]
Przyjmuję dkat = 0,8 [m]
dkat>dobl
2⋅![]()
=2⋅0,502 = 1,005 [m2]
Fkat=1,005[m2]
Fkat>Fobl
Sprawdzam czy vrzecz<vdop
![]()
vrzecz = 1,2 [m3⋅s-1]
Vrzecz<Vdop
Warunek został spełniony.
Obliczenie strat na przepuście.
Straty na przepuści powstają na wskutek:
Zmiany prędkości wody dopływającej i prędkości wody odpływającej
h1=![]()
[m]
Zmiany prędkości wody w rurociągu
h2=![]()
[m]
Strat na wlocie
h3=![]()
[m]
Oporów tarcia dla rurociągu
h4![]()
Ze względu na małą wartość pomijamy straty wynikające ze zmiany prędkości dopływającej i odpływającej. Biorąc pod uwagę w/w czynniki suma strat wyraża się wzorem:
![]()
[m]
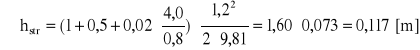
Σ hstr = 0,117 [m]
Następnie sprawdzam warunek czy:
t + hstr < h - s
0,8 + 0,117 < 1,30 - 0,30
0,917 < 1,0
Warunek został spełniony
Ostatecznie przyjmuję przepust kołowy z dwoma rurami o średnicy 2∅ = 0,8[m]
Obliczenia wykonał: Bogusław Paśko
Normy odpływów jednostkowych do wymiarowania zbieraczy w l⋅s-1⋅ha-1.
- tab. 5.57. dr hab. P. Prochal „Podstawy melioracji rolnych” t.1 PWR i L Warszawa 1986 r.)
Rodzaj gleby |
Spadek terenu ‰ |
Norma odpływu - przy opadach rocznych mm |
||||||
|
|
500 |
600 |
700 |
800 |
900 |
1000 |
> 1000 |
Gleby ciężkie zawierające powyżej 50 % części o średnicy < 0,02 mm |
do 20 |
0,40 |
0,45 |
0,60 |
0,80 |
1,20 |
1,50 |
1,80 |
|
20 - 40 |
0,35 |
0,40 |
0,55 |
|
|
|
|
|
> 40 |
0,30 |
0,35 |
0,50 |
|
|
|
|
Gleby średnie i lekkie zawierające 20 - 50 % o średnicy < 0,02 mm |
do 20 |
0,45 |
0,50 |
0,65 |
0,85 |
1,50 |
1,80 |
2,00 |
|
20 - 40 |
0,40 |
0,45 |
0,60 |
|
|
|
|
|
> 40 |
0,35 |
0,40 |
0,55 |
|
|
|
|
Gleby zawierające poniżej 20 % części o średnicy < 0,02 mm |
do 20 |
0,50 |
0,55 |
0,70 |
0,90 |
1,50 |
1,80 |
2,00 |
|
20 - 40 |
0,45 |
0,50 |
0,65 |
|
|
|
|
|
> 40 |
0,45 |
0,50 |
0,65 |
|
|
|
|
* Do ustalenia średnic zbieraczy należy przyjmować normę odpływu z dokładnością do 0,05 l⋅s-1⋅ha-1
Dla opadu 656 mm i średniego spadku terenu 32 ‰ przyjęto normę odpływu q = 0,6 l⋅s-1⋅ha-1
Obliczenia wykonał: Bogusław Paśko
b = 0.5 m
t = 1,0 m
h = 1,30 m
0
0
-10
+10
+5
+10
-5
∑hstr.
+1
i = 5%°
V1
V
d
h
L =5,0 [m]
Wyszukiwarka
Podobne podstrony:
SPRAW B1, Skrypty, UR - materiały ze studiów, studia, studia, 3 BOGDAN, ROK3~1, ODWODN~1
Jaz obl B1, Skrypty, UR - materiały ze studiów, studia, studia, 4 BOGDAN, Semestr I, Budownictwo wod
dom0, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 3, SEMESTR VI, Woiągi
Kopia Opis techniczny B, Skrypty, UR - materiały ze studiów, studia, studia, 4 STASZEK, Semestr II,
KOSZULKA, Skrypty, UR - materiały ze studiów, studia, studia, 3 STASZEK, Mechanika budowli
zapotrzebowanie, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr
crossgosp, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 3, SEMESTR V, Woi
ściana2, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VII, Żel
ściana3, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VII, Żel
dom1, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 3, SEMESTR VI, Woiągi
Cwiczenie 1, Skrypty, UR - materiały ze studiów, studia, studia, 3 STASZEK, Woiągi
ĆW.3.PKT.2, Skrypty, UR - materiały ze studiów, studia, Hydrologia-sylwek, CW3
kubaturap, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VII, N
TABELA CODZIENNYCH STANÓW WODY W ROKU 1973, Skrypty, UR - materiały ze studiów, studia, Hydrologia-s
Cwicz1, Skrypty, UR - materiały ze studiów, studia, studia, Bastek, Studia, Rok 4, Semestr VIII, Bud
Część obliczeniowa1, Skrypty, UR - materiały ze studiów, studia, studia, 4 BOGDAN, Semestr II, Wiejs
ZAPORA~7, Skrypty, UR - materiały ze studiów, studia, studia, 3 STASZEK, Zapory
1a, Skrypty, UR - materiały ze studiów, studia, studia, Błażej, Semestr I
więcej podobnych podstron