1. Wyznaczanie odpowiedzi skokowej układu I rzędu

Ćwiczenie 1:

- Wyznaczyć odp. układu I rzędu dla następujących warunków

a) zmiana warunku początkowego y_1:= - 3 (pozostałe dane bez zmian x=(n) a1:= - 0.5 )

b) zmiana mnożnika b=2 (pozostałe dane bez zmian x=(n) a1:=-0.5 y_1=0)

c) zmiana współczynnika równania a1 = - 4/5 (pozostałe dane bez zmian x=(n) b=1 y_1=0)

d) zmiana wspólczynnika równania a1 = 1/4 (pozostałe dane bez zmian x=(n) b=1 y_1= -4 )

e) zmiana wymuszenia (opóźnienie) x=(n-2) ( dane a1= -0.5 b=1 y_1=0 )

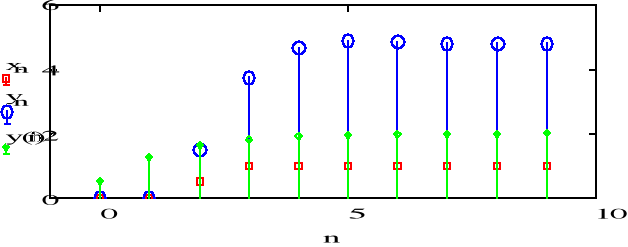
f) zmiana wymuszenia x=13sin( n) ( dane a1= -0.5 b=1 y_1=0 ustawić N=20)

Zapisać równanie rekurencyjne i narysować schemat blokowy dla podpunków b,c,d

Jak zmienia się kształt sygnału oraz jego położenie względem wykresu w przykładzie

Jaki jest stan ustalony odpowiedzi. Jaki ma związek z wsp. a1 i b. Jak wsp. a1 i b wpływają na

rozwiazanie i kształt odpowiedzi.

Jak warunek początkowy wpływa na odpowiedź układu

a)

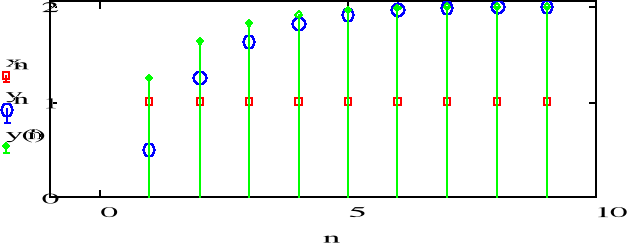
b)

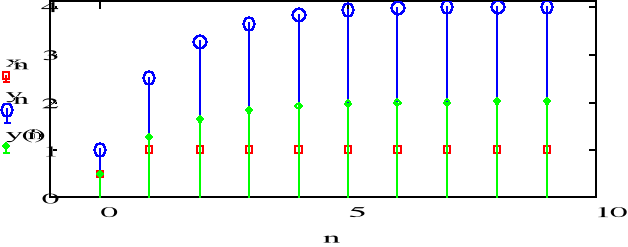
-równanie rekurencyjne.

c)

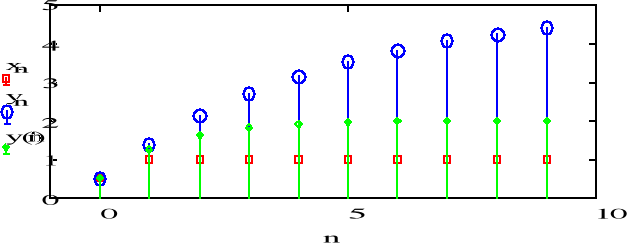
-równanie rekurencyjne.

d)

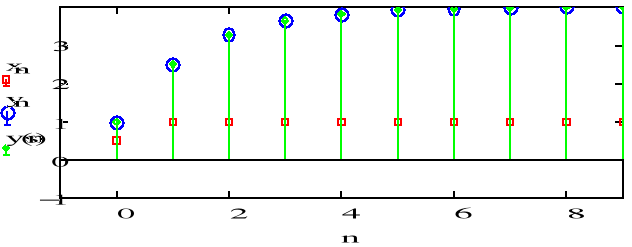
-równanie rekurencyjne.

e)

f)

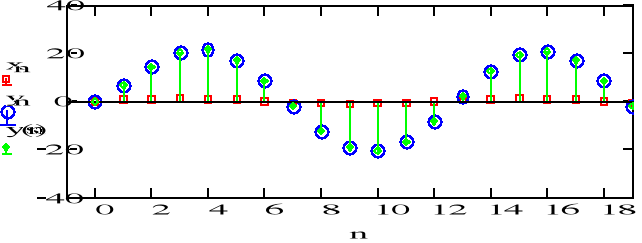
Odpowiedź sygnału dąży do stałej wartości. Im większy jest mnożnik sygnału wejściowego, tym większa wysokość sygnału odpowiedzi. Zwiększenie wartości wsp. a1 powoduje zmniejszenie nachylenia sygnału odpowiedzi. Im większa jest wartość warunku początkowego, tym większa początkowa wartość odpowiedzi. Wartość y zależy od wartości pierwszego sygnału odpowiedzi.

2) Wyznaczanie odpowiedzi impulsowej układu I rzędu

Ćwiczenie 2:

- Wyznaczyć odp. impusową układu I rzędu dla następujących warunków

a) zmiana warunku początkowego y_1:= 4 (pozostałe dane bez zmian x=(n) a1:= -0.5 )

b) zmiana warunku poczatkowego y_1:= -4 (pozostałe dane bez zmian x=(n) a1:= -0.5 )

c) zmiana współczynnika równania a1 = -4/5 (pozostałe dane bez zmian x=(n) b=1 y_1=0)

d) zmiana wspólczynnika równania a1 = 3/4 (pozostałe dane bez zmian x=(n) b=1 y_1=0 )

e) zamiana wymuszenia (opóźnienie) x=(n-2) ( dane a1= -0.5 b=1 y_1=0 )

f) zmiana wymuszenia (opóźnienie) x=(n-2) ( dane a1= -0.5 b=1 y_1=4 )

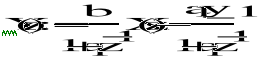
Napisać równanie rekurencyjne i narysować schemat blokowy dla podpunktów c,d i wyznaczyć transmitancję układu H(z)

Jak zmienia się kształt sygnału oraz jego położenie względem wykresu w przykładzie

Jaka jest wartość odpowiedzi dla dużych n.

Jak wsp. a1 wpływa na rozwiazanie i kształt odpowiedzi.

Jak warunek początkowy wpływa na odpowiedź układu.

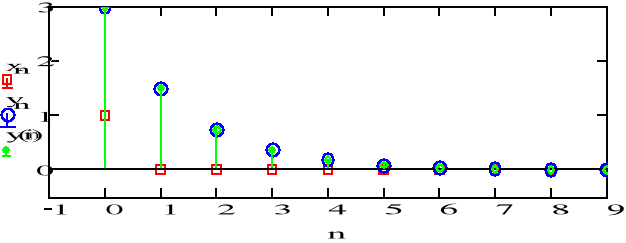
a)

y_1:= 4

x=d(n)

a1:= -0.5

b)

y_1:= -4

x=d(n)

a1:= -0.5

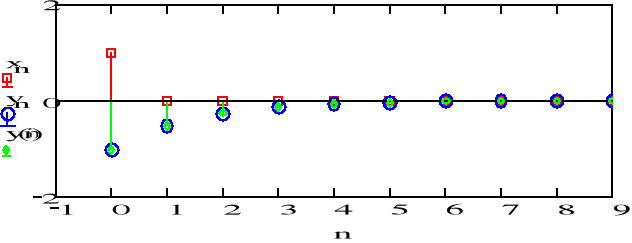
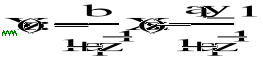
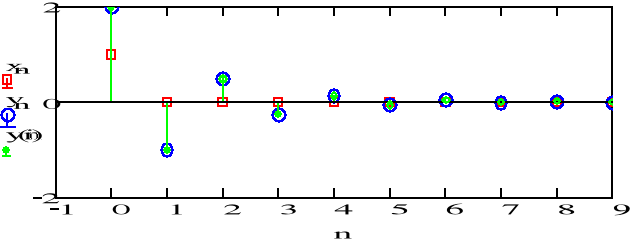
c)

a1 = -4/5

x=δ(n)

b=1

y_1=0

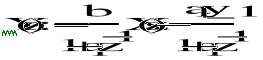
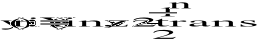
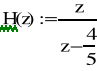
- transmitancja

d)

a1 = 3/4

x=δ(n)

b=1

y_1=0

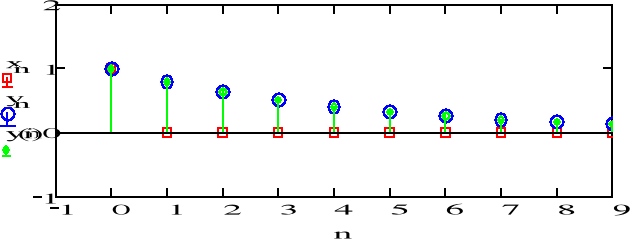
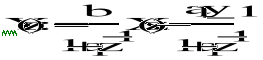
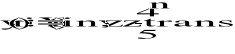
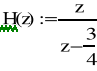
- transmitancja

e)

x=δ(n-2)

a1= -0.5

b=1

y_1=0

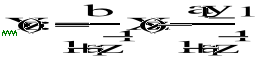
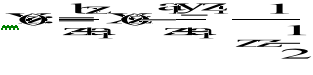
f)

a1= -0.5

b=1

y_1=4

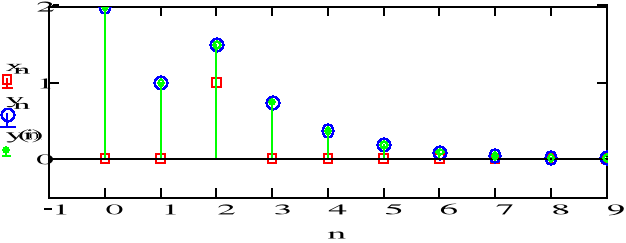
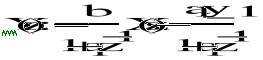
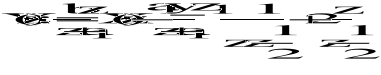
Sygnał jest coraz mniejszy, dąży do zera. Od wsp. a1 zależy czy wykres jest nad, czy pod osią. Warunek początkowy wpływa na to, od jakiej wartości rozpoczyna się sygnał odpowiedzi.

3) Wyznaczanie odpowiedzi skokowej układu II rzędu

Ćwiczenie 3:

- Wyznaczyć odp. układu II rzędu (dwoma metodami) dla następujących warunków (dla a1 = -3/4 a2 = 1/8 )

a) zmiana jednego warunku początkowego y_1:= - 2 (pozostałe dane bez zmian y_2=0)

b) zmiana dwóch warunków początkowych y_1:= -2 i y_2= 8 )

c) zmiana mnożnika b=3 ( y_1=y_2=0)

d) zmiana wymuszenia (opóznienie o 2 ) x=(n-2) ( dane y_1=y_2=0 )

e) zmiana wymuszenia (opóznienie o 2 ) x=(n-2) i war.pocz y_1=0 y_2= -10 )

f) zmiana współczynników równania a1 = 4/5 a2 = 1/2 ( dane x=(n) b=1 y_1=y_2=0 )

g) zamiana wymuszenia x(n)=sin(pi/6 n) ( dane a1= -3/4 a2=1/8 y_1=y_2=0 )

Narysować schemat blokowy i napisać równanie rekurencyjne dla podpunków c, f

Jak zmienia się kształt sygnału oraz jego położenie względem wykresu w przykładzie

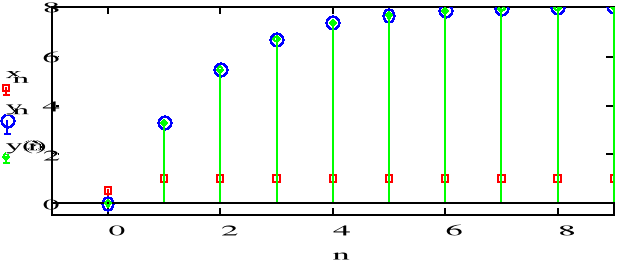
a)

DRUGA metoda - funkcja rekurencyjna

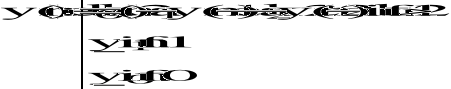
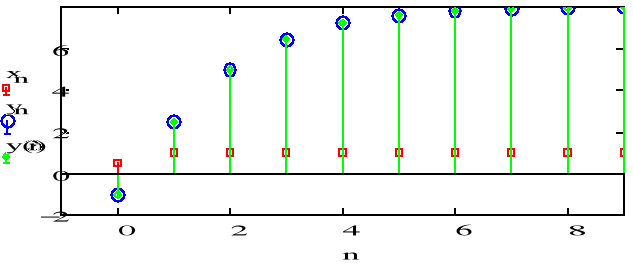
b)

DRUGA metoda - funkcja rekurencyjna

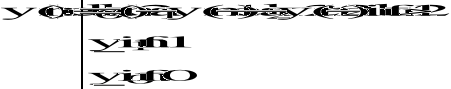
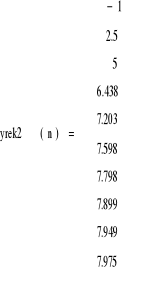
c)

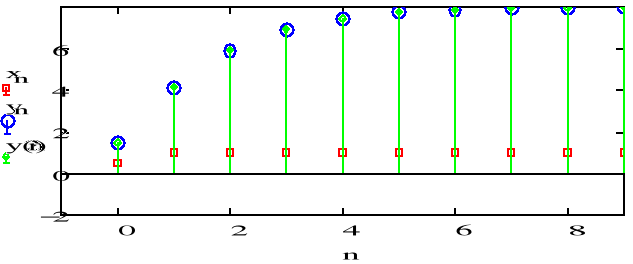
DRUGA metoda - funkcja rekurencyjna

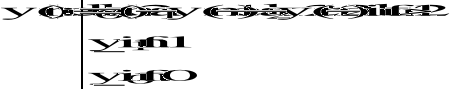
-równanie rekurencyjne.

d)

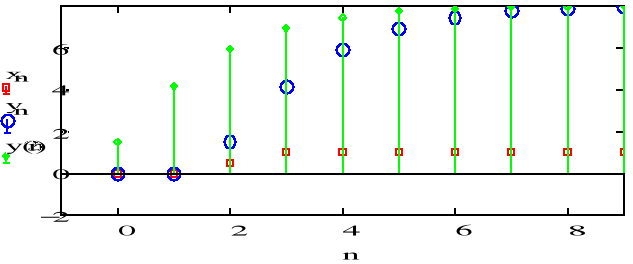
DRUGA metoda - funkcja rekurencyjna

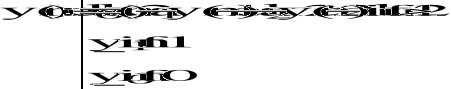
e)

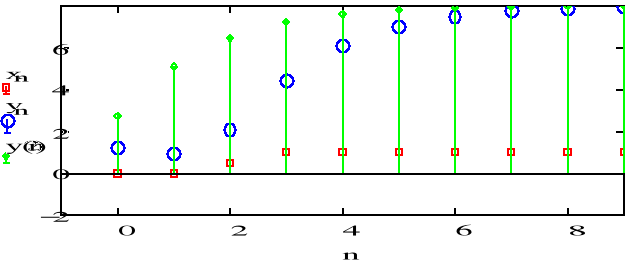
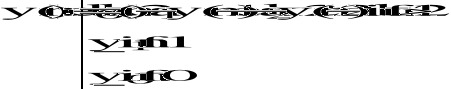
f)

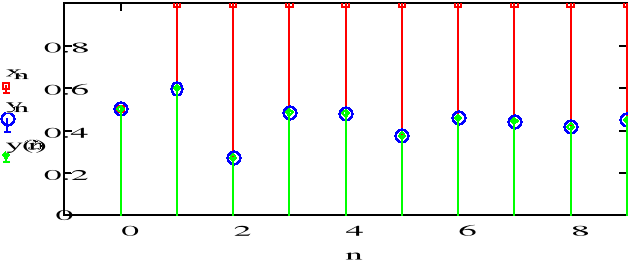
DRUGA metoda - funkcja rekurencyjna

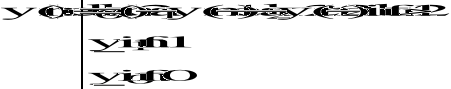
-równanie rekurencyjne.

g)

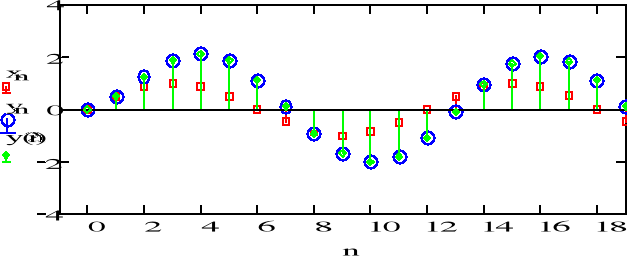
Sygnał dąży do wartości stałej dla dużych n. Wartość ta i kształt wykresu zależą od wsp. a1 i a2.

4) Wyznaczanie odpowiedzi impulsowej układu II rzędu

Ćwiczenie 4:

- Wyznaczyć odp. impusową układu (dwoma metodami) II rzędu dla następujących warunków

a) zmiana jednego warunku początkowego y_1:= 4 i y_2=0

b) zmiana warunków poczatkowych y_1:= -4 i y_2= -14

c) zmiana mnożnika b=3 (pozostałe dane bez zmian x=(n) y_1=y_2=0)

d) zmiana wymuszenia (opóźnienie) x=(n-2) ( dane b=1 y_1=y_2=0 )

e) zmiana wymuszenia (opóźnienie) x=(n-2) ( dane b=1 y_1=4 y_2=0 )

f) zmiana współczynnika równania a1 = 4/5 i a2 = 1/2 (bez zmian: x=(n), b=1, y_1=y_2=0)

Jak zmienia się kształt sygnału oraz jego położenie względem wykresu w przykładzie

Oblicz transmitancję układu H(z)

Jaka jest wartość odpowiedzi dla dużych n.

Jak wsp. a1 , a2 i b wpływają na rozwiazanie i kształt odpowiedzi.

Jak warunki początkowe wpływają na odpowiedź układu.

a)

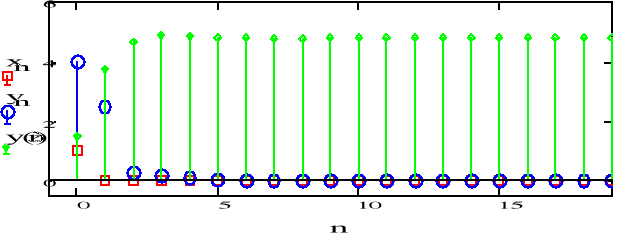
b)

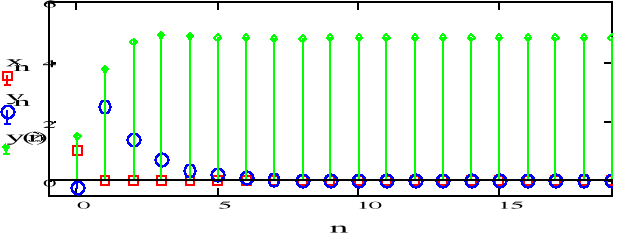
c)

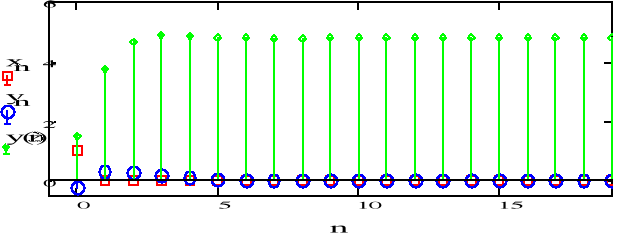
d)

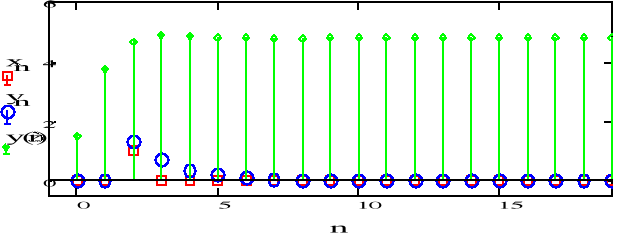
e)

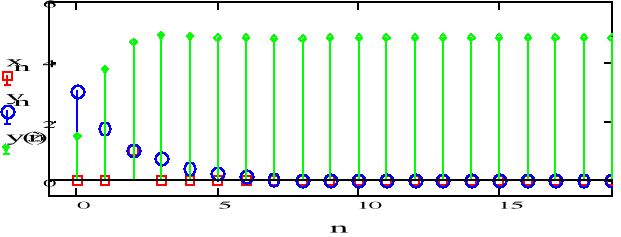
f)

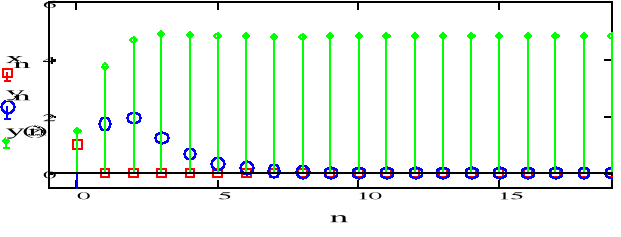
Wraz ze wzrostem n sygnał dąży do zera. Wraz ze wzrostem mnożnika zwiększają się wartości.

Od wsp. a1 i a2 zależy z której strony sygnał dąży do zera

Końcowe wnioski

Odpowiedź I rzędu ma wartość zależną od poprzedniego sygnału, natomiast odpowiedź II rzędu ma

wartość zależną od dwóch poprzednich sygnałów.

---