5. RACHUNEK WEKTOROWY

5.1. Wektor zaczepiony i wektor swobodny

Uporządkowaną parę punktów (A, B), wyznaczającą skierowany odcinek o początku w punkcie A i końcu w punkcie B, nazywamy wektorem zaczepionym w punkcie A i oznaczamy symbolem .

Wektory
to nie te same wektory chociaż AB i BA to ten sam odcinek.

Współrzędne wektora zaczepionego
definiujemy następująco:

= [(xB ; yB ; zB) - (xA ; yA ; zA)] = [xB - xA ; yB - yA ; zB - zA]

Gdy punktem początkowym wektora zaczepionego jest O (0; 0; 0), to współrzędne wektora
są identyczne ze współrzędnymi punktu B.

Przykład: Wyznaczyć współrzędne wektora zaczepionego w punkcie A(2; -1; 3) o końcu w punkcie B(4; 5; -1)

Rozwiązanie:

Otrzymujemy
= [4 - 2; 5 - (-1); -1 - 3] = [2; 6; -4].

Po dokonaniu odejmowań pozostają jako współrzędne wektora trzy liczby. Sytuacja, w której znamy tylko współrzędne wektora, nie opisuje zatem wektora zaczepionego.

Przykład: Dane są punkty A (0; 0; 0), B (1; 2; -1), C (1; 1; 1) i D (2; 3; 0). Obliczyć współrzędne wektorów zaczepionych
.

Rozwiązanie:

= [1 - 0; 2 - 0; -1 - 0] = [1; 2; -1];

= [2 - 1; 3 - 1; 0 - 1] = [1; 2; -1].

Wektory
mają więc takie same współrzędne.

Wektor swobodny jest to zbiór nieskończenie wielu wektorów zaczepionych o takich samych współrzędnych (reprezentantów danego wektora swobodnego).

W dalszych rozważaniach zarówno wektory zaczepione jak i swobodne będziemy krótko nazywać wektorami.

5.2. Współrzędne kartezjańskie wektora

Współrzędnymi kartezjańskimi prostokątnymi wektora
w przyjętym układzie współrzędnych OXYZ, oznaczanymi przez a_x , a_y , a_z , nazywamy współrzędne tego wektora na kolejnych osiach układu, utworzone przez umieszczenie początku wektora
w początku układu współrzędnych.

Rzutując zaczepiony w początku układu współrzędnych wektor, będący reprezentantem wektora swobodnego
, na osie układu współrzędnych, otrzymujemy wzory:

a_x = a cos α , a_y = a cos β , a_z = a cos γ ,

gdzie α , β , γ są to kąty, jakie tworzy wektor
z osiami OX, OY, OZ. Liczba a we wzorach (6.2) to długość wektora
. Współrzędne wektora
można więc zapisać w postaci

= [a_x ; a_y ; a_z] = [a cos α ; a cos β ; a cos γ]

Przykład: Dane są kąty kierunkowe wektora
o długości a =5: α =π/6, β = π/3, λ = π/2. Obliczyć współrzędne wektora
.

Rozwiązanie:

a_x = a cos α = 5 ⋅ cos π/6 = 5 ⋅ cos 30° = 5 ⋅
= 4,33

a_y = a cos β = 5 ⋅ cos π/3 = 5 ⋅ cos 60° = 5 ⋅ 0,5 = 2,50

a_z = a cos γ = 5 ⋅ cos π/2 = 5 ⋅ cos 90° = 5 ⋅ 0 = 0

5.3. Długość wektora. Wersory

Jeśli
= [a_x ; a_y ; a_z], to długość wektora
, oznaczaną
lub a (bez strzałki), obliczamy ze wzoru

Długość wektora
oznaczamy
lub po prostu AB

Przykład: Obliczyć długość wektora o początku w punkcie

A (2; -1; 3) i końcu w punkcie B (4; 2; -1).

Rozwiązanie:

= (4 - 2)² + (2 - (-1))² + (-1 -3)² = 4 + 9 + 16 = 29

Stąd

= AB =
5,385

Wektory o długości równej 1 (wektory jednostkowe), nazywamy wersorami.

Dla każdego wektora (oprócz wektora zerowego) można zbudować odpowiadający mu wersor. Jeżeli
= [a_x ; a_y ; a_z] , to wektor o współrzędnych równych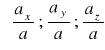
ma długość 1. Stąd dla kosinusów kierunkowych wektora mamy związek:

cos^2 α + cos^2 β + cos^2 γ = 1

Dwa wektory,
, są zgodnie równoległe, gdy współrzędne jednego z tych wektorów można otrzymać ze współrzędnych drugiego, mnożąc je przez liczbę dodatnią. Gdy ta liczba musi być ujemna - mamy wektory przeciwnie równoległe

Wersorem niezerowego wektora
= [a_x , a_{y ,} a_z], oznaczonym
, nazywamy wektor

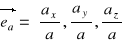
= [ cos α, cos β, cos γ ]

Szczególnymi wersorami są wersory osi układu współrzędnych.

.

5.4. Działania na wektorach

Wprowadzimy następujące działania na wektorach:

- dodawanie wektorów (wynik jest wektorem),

- mnożenie wektora przez liczbę(wynik jest wektorem),

- mnożenie skalarne wektorów (wynik jest skalarem, tzn. liczbą),

- mnożenie wektorowe wektorów (tylko w R³; wynik jest wektorem).

Sumą wektorów = [ax ; ay ; az] oraz = [bx ; by ; bz] jest wektor = [ax + bx ; ay + by ; az + bz]

Przykład:

Obliczyć sumę wektorów:

= [3; -2; 5] ,
= [-1; 4; -7] ,
= [-4; -1; 2]

Rozwiązanie:

= [3 - 1 - 4; -2 + 4 -1; 5 - 7 + 2] = [-2; 1; 0]

Iloczynem różnej od zera liczby λ ∈R i niezerowego wektora nazywamy wektor [λax ; λay ; λaz]

Jest to wektor o długości
, zgodnie równoległy z wektorem
, gdy λ > 0, a przeciwnie równoległy, gdy λ < 0.

Suma iloczynów wektorów i liczb nosi nazwę kombinacji liniowej wektorów i jest - oczywiście - wektorem:

,

i = 1,2, . . . ,n.

Dwa liniowo zależne wektory
(dla których istnieje równa wektorowi zerowemu kombinacja liniowa o współczynnikach różnych od zera, tzn. istnieją λ₁ i λ₂ takie, że
) nazywamy współliniowymi.

Przykład:

Wektory
= [4; -6; 5] i
= [-2; 3; -2,5] są liniowo zależne, gdyż
. Można stąd wyliczyć, że
- czyli są one zgodnie równoległe. Ponieważ są to wektory swobodne, więc można wybrać reprezentanta każdego z nich, zaczepionego np. w punkcie O (0; 0; 0). Wówczas wektory te leżą „jeden na drugim”, przy czym wektor
jest dwa razy dłuższy od wektora
.

Iloczynem skalarnym dwóch niezerowych wektorów , oznaczanym , nazywamy liczbę, określoną następująco: = axbx + ayby + azbz

Iloczyn skalarny niezerowego wektora przez siebie daje wynik równy kwadratowi długości tego wektora:

= a_xa_x + a_ya_y + a_za_z = a² czyli

Tabliczka mnożenia skalarnego wersorów osi:

	i	j	k
i	1	0	0
j	0	1	0
k	0	0	1

Przykład:

Obliczyć iloczyn skalarny wektorów
= [2; 3; -1] i
= [-1; 3; 2].

Rozwiązanie:

= 2⋅ (-1) + 3 ⋅ 3 + (-1) ⋅ 2 = -2 + 9 - 2 = 5

Kątem niezerowych wektorów , oznaczanym , nazywamy kąt, jaki tworzy jeden z tych wektorów z osią zgodnie równoległą do drugiego z wektorów.

Wprowadzimy teraz wzór na kosinus kąta pomiędzy wektorami
. Z rysunku widać, że
, skąd
, albo
, skąd mamy

c² = a² -
+ b²

Z tw. kosinusów mamy:

c² = a² + b² - 2ab cos

Stąd
= 2ab cos

lub

Warunek prostopadłości niezerowych wektorów:

W przypadku wektorów w przestrzeni wektorowej n-wymiarowej, mówimy o ortogonalności: dwa niezerowe wektory są ortogonalne, gdy ich iloczyn skalarny jest równy zero.

Iloczynem wektorowym wektorów
w trójwymiarowej przestrzeni wektorowej, oznaczanym
, nazywamy trzeci wektor,
, mający następujące cechy:

1.

2.

3. trójka wektorów
, zaczepionych w tym samym punkcie, jest ustawiona w takiej samej kolejności, jak wersory osi i, j, k (wektory
tworzą - analogicznie jak wersory osi - tak zwaną prawoskrętną trójkę wektorów).

Dla wersorów osi:

j × i = -k

k × j = -i

i × k = -j

Tabliczka mnożenia wektorowego

Ⴔ	i	j	k
i		k	-j
j	-k		i
k	j	-i

Własności iloczynu wektorowego.

Własności iloczynu wektorowego: 1. (antyprzemienność) 2. (rozdzielność względem dodawania) 3. dla dowolnego λ ∈R 4.

Przykład

Obliczyć iloczyn wektorowy wektorów
= [2; 3; -1] i
= [-1; 3; 2].

Rozwiązanie:

Mamy
= 2i + 3j - k oraz
= -i + 3j +2k

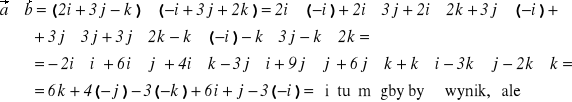
przekształcimy to wyrażenie do postaci następującej:

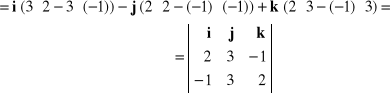
Stąd

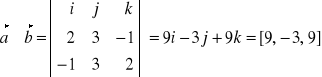
Uogólniając, dla wektorów
= [a_x ; a_y ; a_z] i
= [b_x ; b_y ; b_z]:

PAMIĘTAJMY:

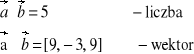
Przykład:

Obliczyć iloczyn wektorowy wektorów

= [2; 3; -1] i
= [-4; -6; 2].

Rozwiązanie:

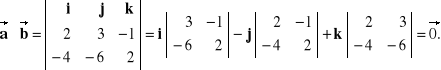
Wektory
 i 
są równoległe.

Wzór na sin kąta między wektorami:

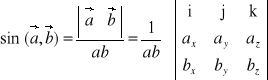
5.5. Rachunek wektorowy - podsumowanie

Wprowadziliśmy dwa podstawowe rodzaje wektorów: wektor zaczepiony i wektor swobodny.

Dla każdego wektora określone zostały:

długość (nazywana także modułem) - tak samo jak długość odcinka,

kierunek - od punktu początkowego do końcowego, a także

zwrot - czyli zgodna lub przeciwna równoległość w stosunku do drugiego wektora lub równoległej osi.

Położenie każdego wektora względem osi układu współrzędnych można określić przy pomocy kątów kierunkowych lub kosinusów kierunkowych.

Wektor o długości jednostkowej otrzymał nazwę „wersor”.

Wersory osi układu współrzędnych oznaczone zostały literami i, j, k. Tworzą one bazę przestrzeni wektorowej trójwymiarowej.

Wprowadzone zostały działania na wektorach:

- dodawanie wektorów (wynik jest wektorem), zapisywane:
;

- mnożenie wektora przez liczbę (wynik jest wektorem), zapisywane bez żadnego znaku między liczbą a wektorem:
R ;

- mnożenie skalarne wektorów (wynik jest skalarem, tzn. liczbą), zapisywane z użyciem kropki:
;

- mnożenie wektorowe wektorów (tylko w R³ ; wynik jest wektorem), zapisywane z użyciem krzyżyka:
.

Określone zostały warunki

- prostopadłości (ortogonalności) wektorów - z wykorzystaniem iloczynu skalarnego

- równoległości wektorów - z wykorzystaniem iloczynu wektorowego;

- współliniowości dwóch wektorów (znikanie ich kombinacji liniowej).

Wprowadzono wzory na kosinus kąta między wektorami ( z wykorzystaniem iloczynu skalarnego) i na sinus kąta między wektorami (z wykorzystaniem modułu iloczynu wektorowego).

5.6. Zadania

1. Dane są punkty A = (1; 1; 3) , B = (0; -1; 4) i C = (3; -5; 0). Wyznaczyć wektory
   

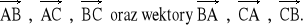
2. Dany jest punkt A = (1; -2; 3). Wyznaczyć punkt B, wiedząc, że a)
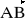
   = [3; 5; -4] , b)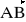
   = [0; 2; 0] , c)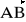
   = [-1; 2; -3].

3. Dane są wektory:
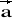
   = [1; 3; 4] ,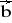
   = [-3; 0; 1] ,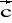
   = [1; 3; 3] oraz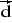
   = [-1; -3; -2]. Wyznaczyć wektor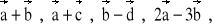                                
   
   .

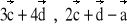
4. Dwa wektory,
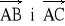
   , mają wspólny początek A ( 1, 2, 0), tę samą długość h = 2 i tworzą kąt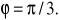
   a) Narysować te wektory oraz ich sumę i różnicę.                                                              b) Narysować kilka wektorów - reprezentantów wektora swobodnego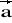
   , którego reprezentantem jest wektor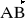
   .          c) Obliczyć moduł sumy i moduł różnicy wektorów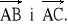
   

5. Dany jest równoległobok o bokach AB, BC, CD, DA. Wyrazić wektory
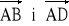
   przez wektory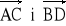
   .

6. Wektory
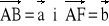
   są sąsiednimi bokami sześciokąta foremnego ABCDEF. Wyrazić wektory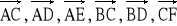
   za pomocą wektorów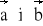
   .

7. Wektory
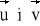
   o długościach u = 1, v = 2, tworzą kąt ϕ = 60°. Obliczyć
   .

8. Wektory
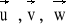
   mają moduły u = 4, v = 2, w = 6 i każde dwa z tych wektorów tworzą kąt równy π/3. Obliczyć:            a)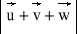
   b)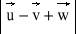
   c)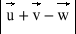
   

9. Dane są trzy liniowo niezależne wektory
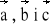
   . Zbadać liniową zależność wektorów.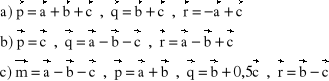
   

10. Mając dane wersory
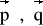
    tworzące kąt 45°, utworzono wektory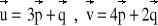
    i zbudowano na tych wektorach równoległobok. Obliczyć długości przekątnych tego równoległoboku.

11. Wyznacz długość wektora
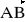
    , jego rzuty na osie układu współrzędnych, kąty, jakie tworzy z osiami współrzędnych dla następujących danych:                                                                    a) A (-1; 0; 3) , B (-2; 5; 0)                                                             b) A (0; 3; -4) , B (4; 0; -3)                                                             c) A (1; 2; -3) , B (-2; -4; 6)

12. Obliczyć wersory wektorów
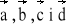
    z zadania 3.

13. Obliczyć iloczyn skalarny wektorów
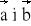
    , wiedząc, że            a) a =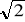
    , b = 3 ,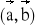
    = π/3                                                      b) a = 2 , b = 5 ,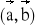
    = 0°                                                      c) a = 2 , b = 5 ,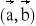
    = 120°                                                      d) a = 1 , b = 5 ,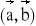
    = π/2                                                      Obliczyć kąt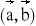
    wiedząc, że                                                      a) a =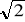
    , b = 5 ,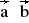
    = 5                                                         b) a = 2 , b = 3 ,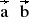
    = 6                                                          c) a = 2 , b = 3 ,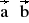
    = 0                                                         d) a = 2 , b = 3 ,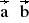
    = -6

14. Dane są punkty A = (0; -1; 3) , B (6; 5; -2) , C = (1; -2; 3).    Wykazać, że
    .

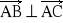
15. Dla jakich wartości parametru m                                             a) wektory [m² + 1; m; 1] i [10; 4; m] są równoległe?                   b) wektory [m²; -3; 0] i [m; m; m +2] są prostopadłe?

16. Zbadać, czy dwa poniższe wektory są równoległe lub prostopadłe. W przypadku równoległości wyrazić jeden z nich przez drugi:                                                                                 a)
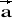
    = [1; 3; 4] ,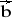
    = [-3; 0; 1]                                                        b)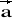
    = [1; 5; 0] ,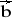
    = [2; 10; 1]                                                         c)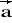
    = [1; 1; 1] ,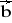
    = [-1; 1; 0]

17. Dane są cztery wektory. Wyrazić jeden z nich jako kombinację liniową pozostałych:                                                                  a)
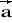
    = [1; 3; 4] ,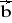
    = [-3; 0; 1] ,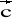
    = [1; 3; 3] ,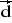
    = [-1; -3; -2]     b)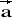
    = [1; 2; 1] ,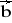
    = [-1; 0; 1] ,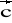
    = [3; 0; 0] ,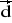
    = [0; 1; -2]      c)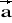
    = [6; 0; 1] ,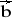
    = [1; 1; 2] ,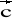
    = [-1; 0; 1] ,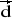
    = [0; 0; 1]      d)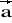
    = [3; 0; 1] ,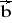
    = [1; 4; -2] ,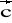
    = [5; 8; -3] ,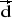
    = [2; -4; 3]

18. Wyznacz wektory prostopadłe do danych dwóch wektorów:      a)
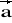
    = [1; 3; 4] ,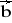
    = [-3; 0; 1]                                         b)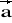
    = [1; 5; 0] ,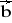
    = [2; 10; 1]                                         c)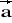
    = [1; 1; 1] ,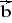
    = [-1; 1; 0]                                         d)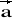
    = [2; -3; 1] ,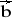
    = -4; 6; -2]

19. Wektor tworzy z osiami OX i OY kąty π/3 i π/4. Obliczyć kąt, który ten wektor tworzy z osią OZ.

20. Zbadać, czy oś o kosinusach kierunkowych 1/2, 1/2,
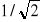
    jest prostopadła do osi o kosinusach kierunkowych 0,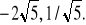
    

21. Oś p ma kosinusy kierunkowe 1/3, -2/3, 2/3. Obliczyć kosinusy kierunkowe osi s, wiedząc, że
    .

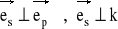
22. Udowodnić, że delta Kroneckera, może być zdefiniowana w trójwymiarowej przestrzeni wektorowej przy wykorzystaniu iloczynu skalarnego wektorów bazy, jeżeli osie układu współrzędnych nazwiemy OX = OX₁ , OY = OX₂ , OZ = OX₃, a wersory osi: i = e₁ , j = e₂ , k = e₃. Rozszerzyć rozumowanie na przestrzeń n-wymiarową.

4.14

B

A •

Z

a_z

O a_y

Y

a_x

α

O a_x X

oś OZ

wersor osi OX: i = [1; 0; 0] k

wersor osi OY: j = [0; 1; 0] j

wersor osi OZ: k = [0; 0; 1] i oś OY

oś OX

Rys. 6.5.

Wersory osi prostokątnego układu współrzędnych.

k

j

i

j -k

i lub po obróceniu

-k o kąt 180 ° i

j

k j

-i lub po obróceniu -i

o kąt 90°

j k

k

-j

i

← współrzędne wektora

← współrzędne wektora

a) Zapis:

b) Zapis: