Teoria Ruchu Pojazdów Samochodowych

Obliczenia trakcyjne pojazdu

Zestaw nr. 53

Wykonał:

Adam Piencek

SRD

sem. IV rok akademicki 2008/09

Założenia w konstrukcji samochodu i podstawowe obliczenia:

Założenia podane przez prowadzącego:

- masa skorupy nadwozia m_s = 300 [kg]

- prędkość maksymalna V_max = 151 [km/h]=41,94 [m/s]

- liczba pasażerów liczba pasażerów - 5

- napęd P (przedni)

Obliczenia wstępne

Długość: 3880mm

Szerokość: 1690mm

Wysokość: 1470mm

Wymiary ogumienia

Dobrałem ogumienie o oznaczeniu: 165/70 R14 81T

Szerokość opony: 165mm

Wysokość profilu opony: 70%*165 [mm] = 115,5 [mm]

R - opona radialna

Promień dynamiczny wynosi: r_d = 0,285 m

Wskaźnik nośności - 81 max 465 [kg]

Wskaźnik prędkości - T max 190 [km/h]

Rozmieszczenie mas w samochodzie:

Lp.	Poszczególne elementy samochodu	mi [kg]	xi [mm]	yi [mm]
1	Masa karoserii	312	2250	800
2	Silnik, skrzynia biegów	180	1100	500
3	Zawieszenie przednie + koła	130	900	300
4	Zawieszenie tylne + koła	95	3300	300
5	Zbiornik paliwa	70	3200	600
6	Przedni fotel + 2 pasażerów	175	2000	550
7	Tylny fotel + 3 pasażerów	255	2800	550
8	Bagaż	50	3700	700

Sylwetka boczna:

Sylwetka przednia:

Obliczam położenie środka masy według poniższych wzorów:

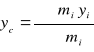
Względem osi x

x_c= 2213 [mm]

Względem osi y

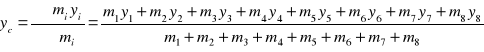
y_c= 569 [mm]

Masa całkowita: m_c= 1267 [kg]

Znając masę pojazdu, rozstaw osi i położenie środka ciężkości możemy wyznaczyć reakcje normalne drogi:

m_c=1267 [kg] l=2600

l₁=2213-900 = 1313 [mm]

l₂=2600-1313 = 1287 [mm]

Oś przednia:
6152,49 [N]

Oś tylna:
[N]

Moc na kołach

Moc na kołach = moc oporów powietrza + moc oporów toczenia

(na poziomej gładkiej nawierzchni w ruchu jednostajnym)

P_k = P_p + P_t [kW]

P_t = m_c · g · f_o · (1 + A_t · V_max²) · V_max

P_p = 0,646 · A_p · C_x · V_max³

gdzie: f_o - współczynnik oporu toczenia f_o = 0,012

A_t - współczynnik dla drogi asfaltowej A_t = 5 · 10^-4 [s²/m²]

C_x - współczynnik oporu powietrza C_x = 0,33

A_p = k · h · b - powierzchnia czołowa samochodu A_p = 1,86 [m2]

k - współczynnik wypełnienia k = 0,75

h - wysokość samochodu h = 1,47 [m]

b - szerokość samochodu b = 1,69 [m]

V_max - prędkość maksymalna

V_max = 151 [km/h] = 41,94 [m/s]

Podstawiając do wzorów otrzymałam:

P_t = 1267 · 9,81 · 0,012 ·(1 + 5 · 10^-4 · 41,94) · 41,94 ≈ 15 [kW]

P_p = 0,646 ·1,86 · 0,33 · 41,94³ ≈ 30 [kW]

P_k = 30 + 15= 45 [kW]

Dobór silnika

gdzie: η_m - sprawność mechaniczna

η_m=η_s · η_b · η_g

η_s - sprawność sprzęgła η_s=0,998

η_b - sprawność skrzyni biegów η_b=0,96

η_g - sprawność przekładni głównej η_g=0,95

Zatem: η_m = 0,99 · 0,96 · 0,95 = 0,9

= 50 [kW]

Silnikiem o zbliżonej mocy jest silnik stosowany w samochodach Chevrolet Aveo o pojemności 1,2 litra. Moc maksymalna tego silnika to 53 kW przy 5 400 obr/min, a maksymalny moment obrotowy 104 Nm przy 4400 obr/min.

P_max = 53 kW n_P = 5400obr/min

T_max = 104 Nm n_T = 4400obr/min

Moment obrotowy dla P_max wyliczam ze wzoru:

T_Pmax = 93,75 Nm

Moc dla T_max wyliczam ze wzoru:

P_Tmax = 47,91 kW

n [obr/min]	1000	1500	2000	2500	3000	3500	4000	4400	5000	5400	6000
Ps [kW]	12	19	24	30	35	40	44	47	52	53	40
Ts [Nm]	89	92	94	96	98	100	102	104	100	95	90

Przełożenie przekładni głównej

Przełożenie całkowite jest równe:

Promień dynamiczny (r_d ) przyjęty na początku wynosi r_d = 0,285 [m] ,tak wiec:

Przełożenie pierwszego biegu

Kryterium przyczepności

gdzie:

λ = 0,87 dla samochodu z napędem klasycznym

μ = 0,7 - współczynnik przyczepności

ƒ₀ = 0,012 - współczynnik oporu toczenia

km/h

Kryterium wzniesień

Maksymalne wzniesienie, jakie może pokonać samochód. Przyjmuję:

współczynnik przyczepności μ=0,7

współczynnik oporów toczenia f_o=0,012

dla napędu klasycznego tangens maksymalnego kąta wzniesienia

określa wzór:

km/h

Kryterium przyspieszeń

gdzie:

- współczynnik nieustalonych warunków pracy silnika

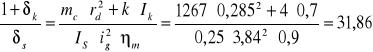
gdzie: k - liczba kół

k = 4

I_s - moment bezwładności ruchomych mas silnika

I_s = 0,25 [kg · m²]

I_k - moment bezwładności kół

I_k = 0,7 [kg · m²]

Podstawiając do i₁ otrzymuję:

km/h

Przełożenie biegu pierwszego i₁ przy założeniu V_1max = 40km/h

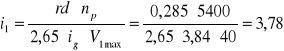
Minimalna liczba biegów oraz przełożenia biegów pośrednich

Minimalna liczba biegów:

Obliczamy ze wzoru:
gdzie:

α_1z - rozpiętość przełożeń skrzynki biegów:

oraz iloraz q_max:

Przyjmuję liczbę biegów z = 5

Dobór przełożeń biegów pośrednich na podstawie prostego postępu geometrycznego

i_z = i₅

i_z-1 = i₄ = i₅ · q

i_z-2 = i₃ = i₅ · q²

i_z-3 = i₂ = i₅ · q³

i_z-4 = i₁ = i₅ · q⁴

gdzie:
; a_1z = 3,87 ;

Zatem:

i₁ = 3,87

i₅ = 1

Dobór przełożeń biegów pośrednich na podstawie podwójnego postępu geometrycznego

i_z = i₅

i_z-1 = i₄ = i₅ · q₁

i_z-2 = i₃ = i₅ · q₁² · q₂

i_z-3 = i₂ = i₅ · q₁³ · q₂³

i_z-4 = i₁ = i₅ · q₁⁴ · q₂⁶

gdzie:

Podstawiając do wzorów otrzymuję następujące przełożenia:

Bilans mocy na kołach na poszczególnych biegach

Wykres ten obrazuje zależność P_k = f(V), czyli zależność mocy na każdym biegu

w funkcji prędkości. Prędkość maksymalna jest osiągana na biegu najwyższym przy mocy maksymalnej na kołach.

Moc na kołach obliczamy ze wzoru: P_k=P_op=P_s∗η_m gdzie η_m=0,9

n [obr/min]	1000	1500	2000	2500	3000	3500	4000	4400	5000	5400	6000
Pk [kW]	11	17	22	27	32	36	40	42	47	48	36
V1	7,35	11,03	14,70	18,38	22,05	25,73	29,40	32,34	36,75	39,70	44,11
V2	10,86	16,28	21,71	27,14	32,57	37,99	43,42	47,76	54,28	58,62	65,13
V3	15,47	23,21	30,95	38,68	46,42	54,16	61,89	68,08	77,37	83,56	92,84
V4	21,22	31,83	42,43	53,04	63,65	74,26	84,87	93,36	106,09	114,57	127,30
V5	28,01	42,01	56,01	70,02	84,02	98,02	112,03	123,23	140,04	151,24	168,04

Wykres trakcyjny

Wykres ten przedstawia zmiany siły napędowej na kołach w funkcji prędkości pojazdu: F_n = f(V) gdzie F_n obliczamy ze wzoru:

gdzie: X_n - siła napędowa

T_s - moment obrotowy

η_m - sprawność mechaniczna

i_g - przełożenie przekładni głównej

i_b - przełożenie biegu

r_d - promień dynamiczny

V dla danej prędkości obrotowej obliczam ze wzoru:

; n_s - prędkość obrotowa

n	1000,00	1500,00	2000,00	2500,00	3000,00	3500,00	4000,00	4400,00	5000,00	5400,00	6000,00
Ts	74,00	78,00	84,00	88,00	92,00	96,00	102,00	104,00	100,00	93,00	84,00
V1	7,35	11,03	14,70	18,38	22,05	25,73	29,40	32,34	36,75	39,70	44,11
Fn	3418,89	3603,70	3880,91	4065,71	4250,52	4435,32	4712,53	4804,93	4620,13	4296,72	3880,91
Fp	1,56	3,51	6,24	9,74	14,03	19,10	24,94	30,18	38,97	45,46	56,12
Fn-Fp	3417,34	3600,19	3874,67	4055,97	4236,49	4416,23	4687,59	4774,75	4581,15	4251,26	3824,79
D1	0,27	0,29	0,31	0,33	0,34	0,36	0,38	0,38	0,37	0,34	0,31
V2	10,86	16,28	21,71	27,14	32,57	37,99	43,42	47,76	54,28	58,62	65,13
Fn	2315,16	2440,30	2628,02	2753,16	2878,30	3003,45	3191,16	3253,73	3128,59	2909,59	2628,02
Fp	3,40	7,65	13,60	21,25	30,60	41,64	54,39	65,82	84,99	99,13	122,38
Fn-Fp	2311,75	2432,65	2614,42	2731,91	2847,71	2961,80	3136,77	3187,92	3043,60	2810,46	2505,63
D2	0,19	0,20	0,21	0,22	0,23	0,24	0,25	0,26	0,24	0,23	0,20
V3	15,47	23,21	30,95	38,68	46,42	54,16	61,89	68,08	77,37	83,56	92,84
Fn	1624,20	1711,99	1843,69	1931,48	2019,27	2107,07	2238,76	2282,66	2194,86	2041,22	1843,69
Fp	6,90	15,54	27,63	43,17	62,16	84,61	110,52	133,72	172,68	201,41	248,66
Fn-Fp	1617,29	1696,45	1816,06	1888,31	1957,11	2022,46	2128,24	2148,93	2022,18	1839,81	1595,03
D3	0,13	0,14	0,15	0,15	0,16	0,16	0,17	0,17	0,16	0,15	0,13
V4	21,22	31,83	42,43	53,04	63,65	74,26	84,87	93,36	106,09	114,57	127,30
Fn	1184,50	1248,53	1344,57	1408,59	1472,62	1536,65	1632,69	1664,70	1600,67	1488,63	1344,57
Fp	12,99	29,22	51,95	81,17	116,88	159,09	207,79	251,43	324,68	378,70	467,54
Fn-Fp	1171,51	1219,30	1292,62	1327,42	1355,74	1377,55	1424,89	1413,27	1276,00	1109,92	877,03
D4	0,09	0,10	0,10	0,11	0,11	0,11	0,11	0,11	0,10	0,09	0,07
V5	28,01	42,01	56,01	70,02	84,02	98,02	112,03	123,23	140,04	151,24	168,04
Fn	897,35	945,85	1018,61	1067,12	1115,62	1164,13	1236,88	1261,14	1212,63	1127,75	1018,61
Fp	22,63	50,91	90,51	141,43	203,66	277,20	362,06	438,09	565,72	659,85	814,63
Fn-Fp	874,71	894,94	928,10	925,69	911,96	886,92	874,82	823,04	646,91	467,89	203,98
D4	0,07	0,07	0,07	0,07	0,07	0,07	0,07	0,07	0,05	0,04	0,02

Wykres charakterystyki dynamicznej

Charakterystyka przedstawia zależność współczynnika dynamicznego w funkcji prędkości pojazdu D=f(V). Wskaźnik dynamiczny obliczam ze wzoru:

Wykres przyspieszeń

Wykres ten przedstawia przebieg przyspieszeń samochodu na poszczególnych biegach w funkcji prędkości pojazdu a=f(V). Wartość przyspieszenia obliczyłem ze wzoru:

Przyjmuję : I_k=0,7[kgm²], I_s=0,25[kgm²], ϑ=0,9

V1	7,35	11,03	14,70	18,38	22,05	25,73	29,40	32,34	36,75	39,70	44,11
D1	0,27	0,29	0,31	0,33	0,34	0,36	0,38	0,38	0,37	0,34	0,31
K1	0,25	0,27	0,29	0,30	0,31	0,33	0,35	0,35	0,34	0,31	0,28
X''1	1,65	1,77	1,90	2,03	2,09	2,22	2,35	2,35	2,28	2,09	1,90
V2	10,86	16,28	21,71	27,14	32,57	37,99	43,42	47,76	54,28	58,62	65,13
D2	0,19	0,20	0,21	0,22	0,23	0,24	0,25	0,26	0,24	0,23	0,20
K2	0,17	0,18	0,19	0,20	0,21	0,22	0,23	0,24	0,22	0,21	0,18
X''2	1,37	1,45	1,52	1,60	1,67	1,75	1,82	1,90	1,74	1,66	1,43
V3	15,47	23,21	30,95	38,68	46,42	54,16	61,89	68,08	77,37	83,56	92,84
D3	0,13	0,14	0,15	0,15	0,16	0,16	0,17	0,17	0,16	0,15	0,13
K3	0,11	0,12	0,13	0,13	0,14	0,14	0,15	0,15	0,14	0,13	0,11
X''3	0,99	1,08	1,16	1,16	1,24	1,23	1,31	1,31	1,22	1,13	0,95
V4	21,22	31,83	42,43	53,04	63,65	74,26	84,87	93,36	106,09	114,57	127,30
D4	0,09	0,10	0,10	0,11	0,11	0,11	0,11	0,11	0,10	0,09	0,07
K4	0,07	0,08	0,08	0,09	0,09	0,09	0,09	0,09	0,08	0,07	0,05
X''4	0,68	0,77	0,76	0,85	0,84	0,83	0,82	0,82	0,71	0,61	0,42
V5	28,01	42,01	56,01	70,02	84,02	98,02	112,03	123,23	140,04	151,24	168,04
D5	0,07	0,07	0,07	0,07	0,07	0,07	0,07	0,07	0,05	0,04	0,02
K5	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,05	0,02	0,01	-0,01
X''5	0,52	0,51	0,50	0,49	0,48	0,47	0,45	0,43	0,23	-0,01	-0,21

Wykres rozpędzania samochodu

Wykres przedstawia zależność prędkości w funkcji czasu V=f(t). Wykreślając ten wykres pominąłem czas przełączania biegów przez kierowcę.

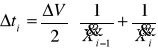
Podsumowanie:

Projektując samochód o zadanych parametrach dobrałem silnik z samochodu Chevrolet Aveo 1.2 . Porównam więc teraz mój projekt właśnie z tym samochodem:

Mój projekt Chevrolet Aveo 1.2

Masa	1276 kg	1000 kg
Moc max.	47,91 kW przy 5400 obr/min	54 kW przy 5400 obr/min
Przyspieszenie 0-100km/h	16,3 s	13,7 s
Moment max	93,75 [Nm] przy 4400 obr/min	104 [Nm] przy 4400 obr/min
Prędkość max	151 km/h	157 km/h

Analizując mój projekt i porównując go do istniejących już produkcji można powiedzieć, że posiadają one zbliżone parametry. Na tle istniejącej konstrukcji musze powiedzieć, że mój samochód mógłby być trochę bardziej dynamiczny i lżejszy.

ZADANIE 2.5

Stosując wymagania ECE (μ=0,8) dobierz współczynnik α. Dla dobranego α wyznacz max. nacisk na pedal hamulca przy którym nie będzie blokowania kół żadnej osi, gdy samochód ten hamuje na oblodzonej nawierzchni o współczynniku przyczepności μ1=0,3. Oblicz drogę hamowania.

DANE : m=1400[kg] μ₁=0,3 V₀=10[m/s] t₀=0,3 [s] l₁=1,2[m] l₂=1,3 [m] h=0,55 [m] k=11,8

γ=μ₁=0,8 = a_n/g → a_n = γ∙g = 0,8∙9,81 = 7,848 [m/s²]

α=Z1n/Z2n

Z_1n= (m∙g∙l₂)/l + (m∙a_n∙h)/l = 9558 [N]

Z_2n= (m∙g∙l₁)/l - (m∙a_n∙h)/l = 4175 [N]

α = 9558/4175 = 2,289

X_1n = μ₁∙[(mg∙l₂)/l + (m∙a_2n∙h)/l] = ?

a_2n = μ₁∙g = 2,943

X_1n = 2414 [N]

S_h = V₀∙t₀ + (V₀²)/2∙a_n = 19,99

ZADANIE 2.2

Wyznacz max. spóźnienie hamowania samochodu na drodze o współczynniku przyczepności μ₁=0,4 dopuszczając blokowanie kół. Optymalna intensywność hamowania uzyskiwana jest na drodze o współczynniku μ₁=0,8.

DANE : m=1500 [kg] μ₁=0,4 μ₂=0,3 α=1,81 l₁=1,33 [m] l₂ =1,17 m h=0,55 m

P→ a_n < (μ₁∙g∙l₂) / {[α/(α+1)]∙l - (l₁∙μ₁)} a_n < 3,302 [m/s²]

T→ a_n < (μ₁∙g∙l₁) / {[1/(α+1)]∙l + (h∙μ₁)} a_n < 4,703 [m/s²]

X_1n = μ₂∙Z_1n

X_2n = μ₁∙Z_2n

a_n = (μ₂∙g∙l₂) / {[α/(α+1)]∙l + (h∙μ₂)} a_n = 2,382 [m/s²]

ZADANIE 2.3.

Jaki powinien być kąt obrotu kierownicy, aby pojazd o podanych parametrach poruszał się z prędkością V po łuku o promieniu R ? Jaką cechę sterowności posiada ten pojazd ? Jak powinien zmieniać się kąt obrotu kierownicy, aby utrzymać zadany tor ruchu przy wzrastającej prędkości ?

DANE : m=1300 kg l₁=1,15 m l₂=1,25 m i_k=1/20 k₁=37000 [N/rad] k₂=32000 [N/rad] V=30 km/h = 8,33 m/s R=30 m

α_k=? = α/i_k

R = l/[tgα+(δ₂-δ₁)] → tgα = l/R - (δ₂-δ₁)

Y₁ = δ₁∙k₁ → δ₁=Y₁/k₁ Y₁=(Y_b∙l₂)/l δ₁=[(Y_b∙l₂)/l] / k₁ = {[(mV²)/R]∙(l₂/l)}/ k₁

Y₂ = δ₂∙k₂ → δ₂=Y₂/k₂ Y₁=(Y_b∙l₁)/l δ₂=[(Y_b∙l₁)/l] / k₂ = {[(mV²)/R]∙(l₁/l)}/ k₂

δ₁=0,0423 < δ₂=0,045 pojazd jest nadsterowny

tgα = (l/R) - δ₂ + δ₁ = 0,077 α=4,403 α_k =88,06

ZADANIE 2.4

Jaki jest promień ruchu pojazdu o danych parametrach, jeśli kąt obrotu kierownicy wynosi αk, a prędkość pojazdu V ? Jaką cechę sterowności posiada ten pojazd ? Uzasadnij.

DANE : m=1300 kg l₁=1,1 m l₂=1,3 m i_k=1/20 k₁=k₂=35000 [N/rad] α_k=180 V=30km/h

R = l / [tgα + (δ₂-δ₁)] → 1/R = [tgα + (δ₂-δ₁)] / l → tgα = (l/R) - (δ₂-δ₁)

δ₁=Y₁/k₁ Y₁=(Y_b∙l₂)/l Y_b=(mV²)/R Y₁= [(m∙V²)/R]∙[l₂/l] → δ₁=(m∙V²∙l₂)/(R∙l∙k₁)

δ₂=Y₂/k₂ Y₂=(Y_b∙l₁)/l Y_b=(mV²)/R Y₂= [(m∙V²)/R]∙[l₁/l] → δ₂=(m∙V²∙l₁)/(R∙l∙k₂)

tgα = (l/R) - δ₂ + δ₁ → R = {l-[(m∙V²∙l₁)/(l∙k₂)]+[(m∙V²∙l₂)/(l∙k₁)]} / tgα

R = 16,15

ZADANIE 2.3. / 2.6.

Pojazd pod wpływem działanie wiatru bocznego wiejącego z jego lewej strony zaczął zbaczać z toru prostoliniowego w prawo. Kierowca, aby utrzymać prostoliniowy kierunek ruchu obrócił koło kierownicy w lewo o kąt 5stopni. Podaj cechę sterowności tego pojazdu oraz podaj jaka była siła wiatru Fw jeśli środek jej naporu znajdował się w odległości lp od osi przedniej.

DANE : k₁=34000 N/rad k₂=38000 N/rad α_k=5st. l=2,5 m i_k=1/24 l_p=1,4

Y₁ ↓_______↓Y₂

↑ F

←→

l_p

Y₁∙l_p = F(l-l_p) → Y₁=F[(l-l_p)/l_p]

Y₂∙l = F∙l_p → Y₂=(F∙l_p)/l

G₁=Y₁/k₁ G₁ = [F∙(l-l_p)]/[l_p∙k₁]

G₂=Y₂/k₂ G₂ = [F∙l_p]/[l∙k₂]

ΔG=G₂-G₁ = F { [l_p/(l∙k₂)] - [(l-l_p)/(l_p∙k₁)] }

Znak różnicy ΔG zależy od wartości { [l_p/(l∙k₂)] - [(l-l_p)/(l_p∙k₁)] }= -0,0084∙10^-3. Wtedy ΔG ma znak ujemny → pojazd jest podsterowny

r_b = l / [tgα+G₂-G₁] gdy r_b=0 pojazd jedzie po linii prostej

tgα+G₂-G₁ = 0 → tgα + {[F∙l_p]/[l∙k₂]} - {[F∙(l-l_p)]/[l_p∙k₁]}= 0

F = - tg α / { [l_p/(l∙k₂)] - [(l-l_p)/(l_p∙k₁) ] }= 10416 N

ZADANIE 2.2.

Określić intensywność hamowania oraz długość drogi hamowania samochodu osobowego na drodze o współczynniku przyczepności μ1 przy założeniu, że hamuje on z max. możliwą intensywnością nie powodującą blokowania kół jezdnych. Przyjąć, że współczynnik rozdziału sił hamowania dobrany jest w oparciu o wymagania ECE i wynosi α.

DANE : l₁=1,3 m l₂=1,2 m h=0,55 m μ₁=0,9 m=1300 kg V₀=100 km/h t_r=0,3 s t_n=0,3 s α=2,3

P→ a_n < (μ₁∙g∙l₂) / {[α/(α+1)]∙l - (h∙μ₁)} a_n < 8,5 [m/s²]

T→ a_n < (μ₁∙g∙l₁) / {[1/(α+1)]∙l + (h∙μ₁)} a_n < 9,16 [m/s²]

X = a_n/g = 8,5/9,81 = 0,87

S_n = V₁∙[t_n+(t_n/2)] + [(V₁²)/(2∙a_n)] = 57,97 m

ZADANIE 2.1./2.6.

Wyznacz długość drogi hamowania przy sile nacisku na pedał hamulca PN wiedząc, że współczynnik rozdział sił hamowania jest stały (równy α) oraz współczynnik proporcjonalności między siłą nacisku na pedał hamulca, a zadaną (całkowitą) siłą hamowania kół osi przedniej wynosi k.

DANE : m=1000 kg l₁=1200 mm l₂=1050 mm h=550 mm k=6,5 α=2,1 μ₁=0,5 μ₂=0,2 V₀=10 m/s t₀=0,3 s P_N=500 N

α=F_N1/F_N2 → F_N2=F_N1/α

k=F_N1/P_N → F_N1=k∙P_N = 6,5∙500=3250 N

a_n=F_N/m → (F_N1+F_N2) / m = (F_N+ F_N1/α) / m = 4,80

S=V₀∙t₀ + [V²/(2∙a_n)] = 13,4 m

Z₁=[(m∙g∙l₂)/l] + [(m∙a_n∙h)/l] Z₂=[(m∙g∙l₁)/l] + [(m∙a_n∙h)/l]

m∙a_n=μ₂∙Z₁ + μ₁∙Z₂

m∙a_n=[(μ₂∙m∙g∙l₂)/l] + [(μ₂∙m∙a_n∙h)/l] + [(μ₁∙m∙g∙l₁)/l] - [(μ₁∙m∙a_n∙h)/l]

***przekształcenia***

a_n=(μ₂∙l₂∙g + μ₁∙l₁∙g) / (l-h∙μ₂+h∙μ₁) = ?

S=V₀∙t₀ + [V²/(2∙a_n)] = 16,2 m

ZADANIE 2.5.

Określ wymagany kąt obrotu kierownicy tak, aby pojazd poruszał się ruchem prostoliniowym przy bocznym wietrze o sile naporu FA wiejącym z prawej jego strony. Podać jaką cechą sterowności charakteryzuje się ten pojazd w tych warunkach. Przyjąć, że środek naporu wiatru znajduje się w odległości lp od osi przedniej.

DANE : k1=34000 N/rad k2=38000 N/rad FA=2500 N ik=1/24 l=2,5 m lp=1,4 m

ZADANIE 2.5

Stosując wymagania ECE (μ=0,8) dobierz współczynnik α. Dla dobranego α wyznacz max. nacisk na pedal hamulca przy którym nie będzie blokowania kół żadnej osi, gdy samochód ten hamuje na oblodzonej nawierzchni o współczynniku przyczepności μ1=0,3. Oblicz drogę hamowania.

DANE : m=1400[kg] μ₁=0,3 V₀=10[m/s] t₀=0,3 [s] l₁=1,2[m] l₂=1,3 [m] h=0,55 [m] k=11,8

γ=μ₁=0,8 = a_n/g → a_n = γ∙g = 0,8∙9,81 = 7,848 [m/s²]

α=Z1n/Z2n

Z_1n= (m∙g∙l₂)/l + (m∙a_n∙h)/l = 9558 [N]

Z_2n= (m∙g∙l₁)/l - (m∙a_n∙h)/l = 4175 [N]

α = 9558/4175 = 2,289

X_1n = μ₁∙[(mg∙l₂)/l + (m∙a_2n∙h)/l] = ?

a_2n = μ₁∙g = 2,943

X_1n = 2414 [N]

S_h = V₀∙t₀ + (V₀²)/2∙a_n = 19,99

ZADANIE 2.2

Wyznacz max. spóźnienie hamowania samochodu na drodze o współczynniku przyczepności μ₁=0,4 dopuszczając blokowanie kół. Optymalna intensywność hamowania uzyskiwana jest na drodze o współczynniku μ₁=0,8.

DANE : m=1500 [kg] μ₁=0,4 μ₂=0,3 α=1,81 l₁=1,33 [m] l₂ =1,17 m h=0,55 m

P→ a_n < (μ₁∙g∙l₂) / {[α/(α+1)]∙l - (l₁∙μ₁)} a_n < 3,302 [m/s²]

T→ a_n < (μ₁∙g∙l₁) / {[1/(α+1)]∙l + (h∙μ₁)} a_n < 4,703 [m/s²]

X_1n = μ₂∙Z_1n

X_2n = μ₁∙Z_2n

a_n = (μ₂∙g∙l₂) / {[α/(α+1)]∙l + (h∙μ₂)} a_n = 2,382 [m/s²]

ZADANIE 2.3.

Jaki powinien być kąt obrotu kierownicy, aby pojazd o podanych parametrach poruszał się z prędkością V po łuku o promieniu R ? Jaką cechę sterowności posiada ten pojazd ? Jak powinien zmieniać się kąt obrotu kierownicy, aby utrzymać zadany tor ruchu przy wzrastającej prędkości ?

DANE : m=1300 kg l₁=1,15 m l₂=1,25 m i_k=1/20 k₁=37000 [N/rad] k₂=32000 [N/rad] V=30 km/h = 8,33 m/s R=30 m

α_k=? = α/i_k

R = l/[tgα+(δ₂-δ₁)] → tgα = l/R - (δ₂-δ₁)

Y₁ = δ₁∙k₁ → δ₁=Y₁/k₁ Y₁=(Y_b∙l₂)/l δ₁=[(Y_b∙l₂)/l] / k₁ = {[(mV²)/R]∙(l₂/l)}/ k₁

Y₂ = δ₂∙k₂ → δ₂=Y₂/k₂ Y₁=(Y_b∙l₁)/l δ₂=[(Y_b∙l₁)/l] / k₂ = {[(mV²)/R]∙(l₁/l)}/ k₂

δ₁=0,0423 < δ₂=0,045 pojazd jest nadsterowny

tgα = (l/R) - δ₂ + δ₁ = 0,077 α=4,403 α_k =88,06

ZADANIE 2.4

Jaki jest promień ruchu pojazdu o danych parametrach, jeśli kąt obrotu kierownicy wynosi αk, a prędkość pojazdu V ? Jaką cechę sterowności posiada ten pojazd ? Uzasadnij.

DANE : m=1300 kg l₁=1,1 m l₂=1,3 m i_k=1/20 k₁=k₂=35000 [N/rad] α_k=180 V=30km/h

R = l / [tgα + (δ₂-δ₁)] → 1/R = [tgα + (δ₂-δ₁)] / l → tgα = (l/R) - (δ₂-δ₁)

δ₁=Y₁/k₁ Y₁=(Y_b∙l₂)/l Y_b=(mV²)/R Y₁= [(m∙V²)/R]∙[l₂/l] → δ₁=(m∙V²∙l₂)/(R∙l∙k₁)

δ₂=Y₂/k₂ Y₂=(Y_b∙l₁)/l Y_b=(mV²)/R Y₂= [(m∙V²)/R]∙[l₁/l] → δ₂=(m∙V²∙l₁)/(R∙l∙k₂)

tgα = (l/R) - δ₂ + δ₁ → R = {l-[(m∙V²∙l₁)/(l∙k₂)]+[(m∙V²∙l₂)/(l∙k₁)]} / tgα

R = 16,15

ZADANIE 2.3. / 2.6.

Pojazd pod wpływem działanie wiatru bocznego wiejącego z jego lewej strony zaczął zbaczać z toru prostoliniowego w prawo. Kierowca, aby utrzymać prostoliniowy kierunek ruchu obrócił koło kierownicy w lewo o kąt 5stopni. Podaj cechę sterowności tego pojazdu oraz podaj jaka była siła wiatru Fw jeśli środek jej naporu znajdował się w odległości lp od osi przedniej.

DANE : k₁=34000 N/rad k₂=38000 N/rad α_k=5st. l=2,5 m i_k=1/24 l_p=1,4

Y₁ ↓_______↓Y₂

↑ F

←→

l_p

Y₁∙l_p = F(l-l_p) → Y₁=F[(l-l_p)/l_p]

Y₂∙l = F∙l_p → Y₂=(F∙l_p)/l

G₁=Y₁/k₁ G₁ = [F∙(l-l_p)]/[l_p∙k₁]

G₂=Y₂/k₂ G₂ = [F∙l_p]/[l∙k₂]

ΔG=G₂-G₁ = F { [l_p/(l∙k₂)] - [(l-l_p)/(l_p∙k₁)] }

Znak różnicy ΔG zależy od wartości { [l_p/(l∙k₂)] - [(l-l_p)/(l_p∙k₁)] }= -0,0084∙10^-3. Wtedy ΔG ma znak ujemny → pojazd jest podsterowny

r_b = l / [tgα+G₂-G₁] gdy r_b=0 pojazd jedzie po linii prostej

tgα+G₂-G₁ = 0 → tgα + {[F∙l_p]/[l∙k₂]} - {[F∙(l-l_p)]/[l_p∙k₁]}= 0

F = - tg α / { [l_p/(l∙k₂)] - [(l-l_p)/(l_p∙k₁) ] }= 10416 N

ZADANIE 2.2.

Określić intensywność hamowania oraz długość drogi hamowania samochodu osobowego na drodze o współczynniku przyczepności μ1 przy założeniu, że hamuje on z max. możliwą intensywnością nie powodującą blokowania kół jezdnych. Przyjąć, że współczynnik rozdziału sił hamowania dobrany jest w oparciu o wymagania ECE i wynosi α.

DANE : l₁=1,3 m l₂=1,2 m h=0,55 m μ₁=0,9 m=1300 kg V₀=100 km/h t_r=0,3 s t_n=0,3 s α=2,3

P→ a_n < (μ₁∙g∙l₂) / {[α/(α+1)]∙l - (h∙μ₁)} a_n < 8,5 [m/s²]

T→ a_n < (μ₁∙g∙l₁) / {[1/(α+1)]∙l + (h∙μ₁)} a_n < 9,16 [m/s²]

X = a_n/g = 8,5/9,81 = 0,87

S_n = V₁∙[t_n+(t_n/2)] + [(V₁²)/(2∙a_n)] = 57,97 m

ZADANIE 2.1./2.6.

Wyznacz długość drogi hamowania przy sile nacisku na pedał hamulca PN wiedząc, że współczynnik rozdział sił hamowania jest stały (równy α) oraz współczynnik proporcjonalności między siłą nacisku na pedał hamulca, a zadaną (całkowitą) siłą hamowania kół osi przedniej wynosi k.

DANE : m=1000 kg l₁=1200 mm l₂=1050 mm h=550 mm k=6,5 α=2,1 μ₁=0,5 μ₂=0,2 V₀=10 m/s t₀=0,3 s P_N=500 N

α=F_N1/F_N2 → F_N2=F_N1/α

k=F_N1/P_N → F_N1=k∙P_N = 6,5∙500=3250 N

a_n=F_N/m → (F_N1+F_N2) / m = (F_N+ F_N1/α) / m = 4,80

S=V₀∙t₀ + [V²/(2∙a_n)] = 13,4 m

Z₁=[(m∙g∙l₂)/l] + [(m∙a_n∙h)/l] Z₂=[(m∙g∙l₁)/l] + [(m∙a_n∙h)/l]

m∙a_n=μ₂∙Z₁ + μ₁∙Z₂

m∙a_n=[(μ₂∙m∙g∙l₂)/l] + [(μ₂∙m∙a_n∙h)/l] + [(μ₁∙m∙g∙l₁)/l] - [(μ₁∙m∙a_n∙h)/l]

***przekształcenia***

a_n=(μ₂∙l₂∙g + μ₁∙l₁∙g) / (l-h∙μ₂+h∙μ₁) = ?

S=V₀∙t₀ + [V²/(2∙a_n)] = 16,2 m

ZADANIE 2.5.

Określ wymagany kąt obrotu kierownicy tak, aby pojazd poruszał się ruchem prostoliniowym przy bocznym wietrze o sile naporu FA wiejącym z prawej jego strony. Podać jaką cechą sterowności charakteryzuje się ten pojazd w tych warunkach. Przyjąć, że środek naporu wiatru znajduje się w odległości lp od osi przedniej.

DANE : k1=34000 N/rad k2=38000 N/rad FA=2500 N ik=1/24 l=2,5 m lp=1,4 m

---