1. Oddziaływania fundamentalne w fizyce

-Oddziaływania fundamentalne są to oddziaływania, które możemy obserwować w przyrodzie dzielą się na :
- Grawitacja - będące zjawiskiem naturalnym polegającym na tym, że wszystkie obiekty posiadające masę oddziałują na siebie wzajemnie przyciągając się.
- Słabe - Jest odpowiedzialne za rozpad beta i związaną z nim radioaktywność oraz rozpad np mionu i cząst dziwnych
- Elektromagnetyczne - stacjonarne pole elektromagnetyczne pozostaje związane ze swoim źródłem, zmienne pole magnetyczne natomiast rozprzestrzenia się w postaci fali elektromagnetycznej.
- Silne - spośród cząstek elementarnych oddziałują tylko kwarki, antykwarki i gluony.

2.Przykłady wielkości fizycznych i ich podział

- Wielkość fizyczna to własność ciała lub zjawiska, którą można porównać ilościowo z taką samą własnością innego ciała lub zjawiska np. długość, masa, natężenie

- dzielimy je na a) podstawowe (dł, czas) b) pochodne (prędkość)

3.Definicje jednostek podstawowych w układzie SI

- Metr(m) - jest to długość drogi przebytej w próżni przez światło w czasie 1/299792458s

- Kilogram(kg) - jest to masa międzynarodowego wzorca jednostki masy przechowywanego w międzynarodowym Biurze Miar w Serves pod Paryżem

- Sekunda(s) - jest to czas równy 9 192 631 770 okresom promieniowania odpowiadającego przejściu między dwoma nadsubtelnymi poziomami stanu podstawowego atomu cezu ¹³³Cs

- Kelwin(K) - jest to 1/273,16 część temperatury termodynamicznej punkty potrójnego wody

- Mol(mol) - jest to liczność materii występująca, gdy liczba cząstek jest równa liczbie zawartych w masie 0,012 kg ¹²C

- Amper(A) - jest natężeniem prądu nie zmieniającego się, który płynąc w dwóch równoległych prostoliniowych przewodach nieskończenie długich o przekroju kołowym znikomo małym, umieszczonych w próżni w odległości 1 m wywołuje między tymi przewodami siłę równą 2*10^-7

- Kandela(Cd) - jest to światłość jaką ma w określonym kierunku źródło emitujące promieniowanie monochromatyczne o częstotliwości 540*10¹²Hz i którego natężenie w tym kierunku jest równe 1/681 W/Sr

- Steradian - jest kątem bryłowym o wierzchołku w środku kuli, wycinającym z jej powierzchni część równą powierzchni kwadratu o boku równym tej kuli

- Radian - jest to płaski kąt zawarty między dwoma promieniami koła wycinającymi z jego okręgu łuk o długości równej promieniowi tego koła.

4.Wielkości wektorowe i skalarne

- Skalarne(posiadają tylko wartość) : masa, objętość, czas, droga, ładunek, praca, moc

- Wektorowe(posiadają : zwrot, kierunek, punkt przyłożenia) : prędkość, przyspieszenie, siła, moment siły, pęd

5.Dodawanie i mnożenie wektorów

- Dodawanie wektorów możemy wykonać techniką graficzną, lub przez dodanie składowych tego wektor

- mnożenie wektorów

ILOCZYN SKALARNY

ILOCZYN WEKTOROWY

6.Kinematyka -Opisuje ruch ciała

Definicja ruchu - Przez ruch ciała rozumiemy zmiany jego położeni względem układu odniesienia

Rodzaje ruchu - Postępowy - wszystkie punkty ciała poruszają się po takich samych torach

- Obrotowy - tory poszczególnych punktów ciała są okręgami współśrodkowymi

Prędkość średnia, chwilowa

- śr:

- ch:

Ruch prostoliniowy jednostajny

Ruch prostoliniowy jednostajnie zmienny

Przyspieszenie średnie, chwilowe

- śr:

- ch:

Ruch krzywoliniowy

Wektor wodzący Położenie punktu P można opisac za pomocą wektora, którego początek w punkcie (0,0) a koniec w P., nazywamy go wodzącym , jest on funkcją czasu r=r(t),

Równoważne równania skalarne: x=x(t), y=y(t), z=z(t) przedstawiają współrzędne w.wodz. jako funkcję czasu

Tor kolejne położenia jakie zajmuje pkt w układzi

Prędkość v=dr/dt pochodzna w.wodzącego wzg. Czasu, wektor prędk styczny do toru, vx=dx/dt, vy, vz

Przyspieszenie a=dv/dt=d^x/dt^, analogicznie ax,y,z

Rzut ukośny Ruch ciała, któremu nadano prędkość początkową V₀ skierowaną pod kątem α do poziomu.

W kierunku poziomym ruch jest jednostajny ze stała prędkością: równanie poziome x = V_0x * t; pionowe:
- w kierunku poziomym występuje stałe przyspieszenie ziemskie g skierowane w dół w kierunku ujemnym osi y oraz prędkość początkowa V_0y w kierunku dodatnim osi y.

Współrzędne dowolnego punktu na krzywej toru w dowolnym czasie t:

Równanie toru:

Zasięg rzutu:
;

maksymalna wysokość:
; gdy α = 45 to zasięg będzie największy; dla kątów α i 90 - α zasięg jest taki sam;

całkowity czas:

Rzut poziomy Prędkość ciała w każdym punkcie toru jest wypadkową prędkości stałej V₀ w kierunku poziomym i prędkości pionowej V_y= g * t. Prędkość wypadkowa jest styczna do toru.

Równanie toru: poziomo - x = V₀ * t;

pionowo -
,

cały tor -

Zasięg poziomy rzutu:

Ruch po okręgu

- prędkość liniowa, T - okres

[
],
- prędkość kątowa

- częstość obrotów [
] = 1 Hz ;

Przyspieszenie dośrodkowe:
- ma taki sam kierunek jak
, czyli ma kierunek zgodny z promieniem i zwrot do środka koła;
; z okresem -

[
] - moment pędu

Cztery palce składamy w kierunku ruchu ciała, to wyciągnięty kciuk określa zwrot momentu pędu; Jest on prostopadły do okręgu.

7.Dynamika punktu materialnego

Pierwsza zasada dynamiki- Ciała nie poddane oddziaływaniu żadnych innych ciał albo pozostaje w spoczynku, albo pozostaje spoczynku albo porusza się ruchem jednostajnym prostoliniowym tzw. Zasada bezwładności

Druga zasada dynamiki- siła działająca na ciało jest równa iloczynowi przyspieszenia i masy tego ciała

F = ma a = F/m

Trzecia zasada dynamiki- Jeżeli ciało A działa na ciało B pewną siła F_AB to ciało B działa na ciało A siłą F_BA równą co do wartości lecz przeciwnie skierowaną (zasada akcji i reakcji)

Pęd- Pędem ciała nazywamy iloczyn jego masy i prędkości

Przykłady sił występujących w mechanice

- siła sprężystości

- siła tarcia

- współ. tarcia N- Nacisk ciała na podłoże

Dynamika ruchu punktu materialnego po okręgu

s=
;
= d
/dt [rad/s], v=
r [m/s]
Okres ruchu- czas potrzebny na przebycie drogi kątowej 2

T= 2
/

f- częstotliwość, liczba obiegów pkt. Na jednostkę czasu
f=1/T [1/s]=[Hz]


Przyspieszenie kątowe:

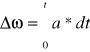
Przyspieszenie normalne i styczne- odpowiedzialne za zmianę wartości v(wektor), odpowiada za zmiane kier. V
Dynamika pkt. Mat. Po okręgu:

Fn=m*a_n=m*v²/r

Praca, moc, energia mechaniczna, energia

Kinetyczna:
Praca: dW=F*ds.= F*cos αds=Fds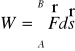

[J]=1N*m=1 kg* m²/s²
Moc:

[W]=1J/s

Energia: Kinetyczna (masa, prędkość), Potencjalna( masa i położenie);

Energia potencjalna- ciała w pkt. P wzg. Pkt. 0 nazywamy pracę jaka wskazuję siła zachowawcza przy przesunięciu tego ciała od pkt. P do pkt. 0

Grawitacyjna en. Pot. Ep=mgh

Potencjalna en. Sprężystości Ep=1/2kx²

Siły zachowawcze

Siłę nazywamy zachowawczą albo potencjalną jeżeli jej praca po dowolnym torze zamkniętym jest równa zeru

Praca w polu sił ciężkości

Praca siły zachowawczej, nie zależy od kształtu drogi a tylko od wyboru pkt początkowego i końcowego

Grawitacyjna energia potencjalna

Ep = m*g*h

Potencjalna energia sprężystości

Ep = ½*k*x²

8.Dynamika układu punktów materialnych

Środek masy

Twierdzenie o ruchu środka masy

- środek masy punktów materialnych porusza się tak jak punkt materialny o masie równej całkowitej masie układu, na którym działa F_z równa wypadkowej sił zewnętrznych

Siły zewnętrzne i wewnętrzne

Dynamika bryły sztywnej, rodzaje ruchów bryły sztywnej

- Bryła sztywna - jest to ciało, które pod działaniem sił nie ulega odkształceniom tzn, odległość dwóch dowolnych punktów takiego ciała pozostają stała.

- Rodzaje ruchów :

- Ruch postępowy punktu materialnego jest to każdy ruch tego punktu opisywany przy użyciu wielkości charakterystycznych dla ruchu postępowego

- Ruch obrotowy to taki ruch, w którym wszystkie punkty bryły poruszają się po okręgach o środkach leżących na jednej prostej zwanej osią obrotu.

Moment siły- Wielkość wywołująca ruch obrotowy nazywamy momentem siły. Moment siły F względem punktu O osi obrotu nazywamy iloczyn wektorowy wektora wodzącego i punktu przyłożenia siły F i tej siły

Moment bezwładności - momentem bezwładności I bryły względem danej osi nazywamy sumę iloczynów mas m_i poszczególnych punktów bryły i kwadratów R_i ich odległości od danej osi

Moment bezwładności niektórych brył:

Kula o r = R

Walec o r = R

Pręt o dł. l

Obręcz o r = R

Twierdzenie Steinera

- Moment bezwładności I bryły względem dowolnej osi jest równy sumie momentu bezwładności I₀ względem osi równoległej przechodzącej przez środek masy bryły oraz iloczynu masy tej były i kwadratu odległości „a” obu osi

Moment pędu - Dla punktu materialnego : L = r x Mv

L = rmV=mr²

L = mr²

Dla bryły L =

L = I

Moment pędu bryły równa się iloczynowi jej prędkości kątowej
i momentu bezwładności I

Momentem pędu L bryły względem czasu równa się momentowi M działającej na tę bryłę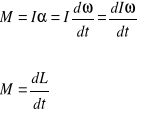

Pierwsza, druga, trzecia zasada dynamiki ruchu obrotowego

- I zasada ruchu obrotowego - Bryła sztywna nie poddana działaniu momentu siły pozostaje nieruchoma lub wykonuje ruch obrotowy jednostajny

- II zasada ruchu obrotowego - Jeżeli bryła A działa na bryłę B momentem siły M_AB to B działa na A momentem siły M_BA równym co do wartości i przeciwnie skierowanym

Energia kinetyczna ruchu obrotowego

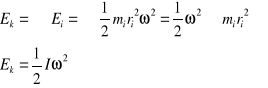
- Energia kinetyczna ruchu obrotowego równa się połowie iloczynu momentu bezwładności i kwadratu prędkości kątowej

Toczenie się bryły Ek= Ek post+ Ek obrot= 1/2mv^+1/2I'omega'^

9.Zasady zachowania w mechanice

Zasada zachowania energii mechanicznej

- Układ odosobniony to taki układ, na który nie działają siły zewnętrzne. Jeżeli siły te są zachowawcze to taki układ będziemy nazywać układem zachowawczym.

Zasada zachowania pędu

- Jeżeli wypadkowa sił zewnętrznych działających na układ jest równa zeru to pęd całkowity tego układu jest stały.

Zasada zachowania momentu pędu - krętu

- Jeżeli moment wypadkowy sił zewnętrznych działających na układ równy jest zeru, to kąt całkowity tego układu jest stały.

10.Siły bezwładności

Inercjalne i nieinercjalne układy odniesienia

- Inercjalne - układ odniesienia, w którym ciało nie poddane działaniu sił pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym nazywamy układem inercjalnym. Każdy układ poruszający się względem układu inercjalnego ruchem jednostajnym i prostoliniowym jest też układem inercjalnym

- Nieinercjalny - układ odniesienia poruszający się ruchem niejednostajnym względem jakiegokolwiek inercjalnego układu odniesienia.

Przykłady sił bezwładności

- bezwładności - siła będąca wynikiem przyspieszenia układu. Siła nie jest oddziaływaniem z innymi ciałami, siła ta występuje tylko w nieinercjalnym układzie

- odśrodkowa - siła będąca wynikiem poruszania się po okręgu siła działająca na zewnątrz

- Siła coriolisa - działa na ciało poruszające się ruchem postępowym w obracającym się układzie odniesienia.

11.Grawitacja

Prawo grawitacji- powszechnego ciążenia

- Dwa punkty materialne o masach m₁ i m₂ przyciągają się wzajemnie siła proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu ich odległości :

Ciężar ciał. Przyspieszenie ziemskie. Pole grawitacyjne

- Ciężar ciał - przyspieszenie ziemskie ciężarem ciała nazywamy siłę jaką ciało materialne jest przyciągane przez ziemię:

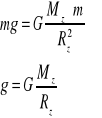
Wyznaczanie masy Ziemi : Dla R_z=6400 km g=9,81 m/s² M_z=6 10²⁴ kg

- Pole grawitacyjne - w przestrzeni otaczającej masę M powstaje pole grawitacyjne o takiej własności, że na masę próbną m umieszczoną w tym polu działa siła

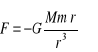
- Przyspieszenie ziemskie - przyspieszenie grawitacyjne ciał swobodnie spadających na Ziemię bez oporów ruchu.

Energia potencjalna pola grawitacyjnego

-

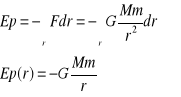
Potencjałem pola grawitacyjnego nazywamy stosunek energii potencjalnej masy próbnej m do wartości tej mas

Prędkości kosmiczne

- Pierwszą prędkością kosmiczną nazywamy najmniejszą możliwą prędkość jaką musi mieć punkt materialny swobodnie krążący wokół ziemi

Siła odśrodkowa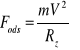

Siła grawitacji

WARUNKIEM STABILNOŚCI ORBITY JEST RÓWNOWAGA TYCH SIŁ !!

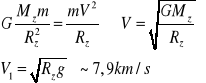
- Druga prędkość kosmiczna nazywana prędkością ucieczki - nazywamy najmniejszą możliwą prędkością jaką musi mieć punkt materialny przy powierzchni Ziemi aby mogło oddalić się od niej w nieskończoność

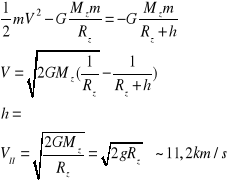
- Trzecią prędkość kosmiczna to prędkość potrzebna do opuszczenia układu słonecznego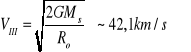

M_s - masa Słońca

R_o - Promień orbity Ziemi

12.Elementy szczególnej teorii względności

Postulaty Einsteina

- Zasada względności - zasada głosząca, że prawa fizyki są jednakowe we wszystkich układach inercjalnych - musi obowiązywać dla wszystkich praw zarówno mechaniki jak i elektrodynamiki

- Niezmienność prędkości światła - prędkość światła w próżni jest taka sama dla wszystkich obserwatorów, taka sama we wszystkich kierunkach i nie zależy od prędkości źródła.

Pomiary prędkości światła

- Pierwszego dokonał Galileusz - Odsłanianie i przesłanianie latarni na oddalonych od siebie wzgórzach

- Ole Romer - 1676 - stwierdził, że światło potrzebuje mniej niż 1 s na przebycie 3000 mil francuskich ( około 13000 km ) - obliczenia na podstawie obserwacji Jowisza

- Armand Fizeau - 1849 - pomiar przy pomocy koła zębatego

- Albert Michelson - 1907 - INTERFERON

Doświadczenie Michelson'a-Morley'a

- MICHELSON-Do określenia prędkości wiatru eteru trzeba porównać prędkość światła w różnych kierunkach. W interferonie( urządzenie potrzebne do doświadczenia) wiązka światła zostaje podzielona półprzezroczystą płytką na dwie prostopadłe wiązki, które po odbiciu od zwierciadeł i powrotnym przejściu przez płytkę trafiają do teleskopu, w którym widać jasne i ciemne prążki jako wynik interferencji obu wiązek. Obraz interferencji zależy od różnicy czasu przebiegu obu wiązek między płytką, a zwierciadłem, bo w pozostałej części drogi światła obie wiązki biegną tą samą dragą.

MICHELSON - MORLEY - Długość drogi światła została zwiększona 10 - krotnie, układ interferonu pływał w korytach wypełnionych rtęcią by zapobiec jakimkolwiek drganiom jednak i to nie wykazało zmian w ich doświadczeniu.

Transformacja Lorentza

- Transformacja Lorentza - umożliwia obliczenie wielkości fizycznych w pewnym układzie odniesienia, jeśli znane są te wielkości w układzie poruszającym się względem pierwszego. Przekształceniu temu ulegają współrzędne czasoprzestrzeni, energia. Wzory zostały wprowadzone w oparciu o założenia, że prędkość światła jest stała i niezależna od prędkości układu.

Transformacja Lorentza - zachowuje odległości w czasoprzestrzeni, zachowany jest interwał, transformacje współrzędnych mają najprostszą postać

Czynnik Lorentza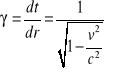

v - prędkość ciała względem danego układu

c - prędkość światła

v/c - prędkość wyrażona w stosunku do prędkości światła

Paradoks bliźniąt

-Na Ziemi( lub w dowolnym punkcie wszechświata przy założeniu, że z miejscem tym związany jest układ inercjalny) rodzą się bliźnięta, jeden z nich pozostaje na Ziemi, a drugi wysyłany szybkim statkiem kosmicznym w przestrzeń kosmiczną( im statek szybszy, tym spodziewamy efekt będzie większy), po pewnym czasie zawraca ląduje na ziemi i spotyka się ze swoim bratem bliźniakiem.

Zgodnie ze szczególną teorią względności czas w poruszającym się układzie odniesienia płynie wolniej ( dylatacja czasu ). Obserwacje bliźniaków przedstawiają się następująco :

1. Bliźniak pozostający na Ziemi spodziewa się, że skoro jego brat - kosmonauta poruszał się względem niego, to po powrocie brat- kosmonauta powinien być młodszy, jeżeli dylatacja czasu jest prawdą .

2. Bliźniak-kosmonauta myśli, że w jego układzie odniesienia to właśnie brat pozostały na Ziemi się poruszał względem niego

WNIOSEK :

Pierwsza odpowiedź prawidłowa - tylko jeden z nich może związać układ inercjalny, a skoro drugi zawraca rakietą to układ przestaje być już tym samym układem.

Masa i energia relatywistyczna

- masa relatywistyczna - jest wielkością względną jej wartość zależy od układu odniesienia, nie jest niezmiennikiem relatywistycznym. Może ona zmieniać się bez zmiany zachodzącej w samym obiekcie fizycznym, wyłącznie przez zmianę układu odniesienia.

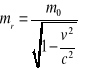
m_r - masa relatywistyczna

m₀ - masa spoczynkowa

v - prędkość ciała względem danego układu

13.Ruch drgający i falowy

-Ruchem drgającym( drganiem lub oscylacją) nazywamy ruch ciała zachodzący wokół stałego położenia równowagi rozróżniamy ruchy drgające :

- okresowe

- nie okresowe

Ruch okresowy PERIODYCZNY to taki ruch, w którym położenie ciała powtarza się w jednakowych odstępach czasu, zwanych okresami drgań T. Dla takiego ruchu położenie punktu materialnego spełnia następujący warunek

x(t)=x(t+T)

Drganie opisane funkcją
nazywamy drganiem harmonicznym gdzie :

A - amplituda drgań

Drgania harmonicznie proste

Drgania złożone

- składanie drgań harmonicznych równoległych o tej samej częstotliwości :

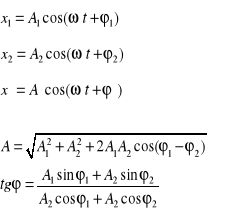
Twierdzenie Fouriera

- Dowolne drganie okresowe x(t) o okresie T jest superpozycją drgań harmonicznych i można je wyrazić szeregiem postaci

Ruch falowy. Rodzaje fal. Prędkości rozchodzenia się fal

- Ruch falowy - nazywamy przenoszenie się zaburzenia w ośrodku. Ruch falowy jest związany z transportem energii przez ośrodek.

- Rodzaje fal - fale Podłużne

- fale Poprzeczne

- fale harmoniczne

- impuls falowy

- fale płaskie

-fale kuliste

- Prędkośc rozchodzenia się fal

Podłużnej w ciele statycznym

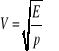
E - moduł Younga p - gęstość ciała

Poprzecznej w ciele stałym

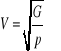
G - moduł sztywności

Podłużnej w cieczy

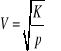
K- moduł ściśliwości ciecz

Podłużnej w gazie

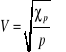
x_p = c_p/c_v p - ciśnienie gazu

Fala harmoniczna płaska. Równanie fali harmonicznej płaskiej

- Fala harmonicznie płaska

- Równanie fali harmonicznej płaskiej

Długością fali
nazywamy odległość dwóch punktów fali o fazach różniących się o 2pi

Zasada Huygensa. Dyfrakcja fal.

- Zasada Huygensa - Każdy punkt do którego dociera czoło fali staje się źródłem elementarnej fali kulistej.

- Dyferencja fali - jest obserwowana, gdy rozmiar obiektu, na którym zachodzi ugięcie jest porównywalny z długością fali.

Interferencja fal. Fale stojące.

- Interferencja - nakładanie się fal - zjawisko nakładania się fal o tych samych długościach, a więc tym samych pulsacjach. W miejscu spotkania fal o przeciwnych fazach następuje wygłuszenie.

- Fala stojąca - powstaje w wyniki interferencji fal biegnących w przeciwnych kierunkach o jednakowej długości i amplitudzie. W - węzeł( miejsce nieruchomości) S- strzałka ( cząstki drgające z największą amplitudą.) położenie W i S nie ulega zmianie. Odległość między sąsiednimi strzałkami i węzami :

Powstaje wzdłuż struny drgającej wewnątrz piszczałek organowych

Fale akustyczne. Źródła fal akustycznych. Dźwięki. Tony. Barwy.

- Podłużne fale mechaniczne mogące rozchodzić się w ciałach stałych, cieczach, gazach

Obejmują częstotliwość 20 Hz - 20 000 Hz

Fale o częstotliwościach:

x<20 Hz - INFRADŹWIĘK,

x>20 000 Hz - ULTRADŹWIĘK

- Źródła fal akustycznych

- Dźwięki

- Tony

- Barwy

Zjawisko Dopplera

- Zmiana odbieranej częstotliwości, gdy źródło i obserwator poruszają się względem siebie - źródło jest nieruchome, zbliżający się obserwator odbiera fale o większej częstotliwości

Źródło nieruchome
obserwator ruchomy

V₀ - obserwator względem źródła

Źródło ruchome, Obserwator nieruchomy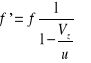

V_z to V źródła

Ultradźwięki i ich zastosowanie

- Fale dźwiękowe których częstotliwość jest zbyt wysoka aby słyszał je człowiek. Umowna granica ultradźwięków to 10 GHz

- Zastosowanie :

- lokacja ultra dźwiękowa

- defektoskopia

- koagulacja

- rozpad cząstek polimerów

- wytwarzanie emulsji, substancji trudno rozpuszczalnych

14.Mechanika cieczy i gazów

Prawo Pascala Ciśnienie zewnętrzne wywierane na ciecz lub gaz jest przenoszone we wszystkich kierunkach jednakowo p=p0 +'ro'gh

Prawo Archimedesa na ciało zanurzone w cieczy działa siła wyporu równa ciężarowi wypartej przez to ciało cieczy W='ro'cieczy*gV

Pływanie ciał na każde ciało działa siła wyporu i ciężkości Q=Vg*'ro', ich wypadkowa wyrażona jest związkiem: R=W-Q, gdy W>Q ciało pływa na powierzchni, W=Q pływa w środu, W<Q tonie

Przepływ cieczy i gazów Ruch płynów nazywamy przepływem. Uporządkowany ruch cząstek płynów poruszających się w jednym kierunku nazywamy strumieniem. Przepływ nazywamy laminarnym gdy nie następuje mieszanie się sąsiednich warstw, turbulentnym jeśli zachodzi mieszanie się poszczególnych warstw płynu.

Równanie ciągłości v1/v2=s2/s1 prędkości cieszy w strumieniu są odwrotnie proporcjonalne do powierzchni przekrojów strumienia

Prawo Bernouliego suma energii kin, poten i ciśnienia jednostki masy ustalonego przepływu cieczy doskonałej jest wielkością stałą p+'ro'v^/2+'ro'gh=const

Przepływ cieczy rzeczywistych i gazów.

Lepkość = tarcie wewn. Procesy dążące do wyrównania prędkości

Wzór Stokes'a F=6pir'eta'v wyraża siłę tarcia wywartą przez ciecz na kulkę o prędkości v, promieniu r, `eta' współczynnik lepkości

Siła Magnusa powstaje zawsze wtedy gdy strumień opływający ciało będzie miał w płaszczyźnie prostopadłej do strumienia i przechodzącej przez to ciało, różne prędkości po przeciwległych str ciała.

15.Termodynamika

a)fenomenologiczna Mkroskopowe wiel charakt. Ukłąd:ciśnienie,temperatura,objętośc,energia,entropia

b) statyczna

mikroskopowe wiel. charakt. Cząski,atomy :prętkość, masa, energia pęd

Zerowa zasada temodynamiki-

Jeżeli ciało AiB są w równowadze termicznej z ciałem C to ciała A i B………nie wiem kurwa obcieło mi notatki

Pomiar temperatury:

a)Zmiana długości pręta

b)Opór elektryczny

c)Ciśnienie gazu

d)Kolor włókna żarówki

Temp termo dynam. - bezwzględna T

Jednostki kelwin

Punkt potrójny wody wynosi 273,16K

Równanie Clapeyrona

pV=nRT p V=NkT

n-liczba moli gazu

R=3,314L/mol

P=ciśnienie

V obj. T-temp

K=R/Na=1,38*10 do -23J/K -stała Boltmana

Na=6,023*10do23-l introgadra

Założenia:

A) cząsteczki gazu można traktować jako pkty mat.

B) znajdują się w szybkim ruchju

c)zderzają się sprężyście ze sobą

d) siły działają tylko w momencie zderzenia

e) V cząsteczek gazu jest zaniedbywalnie mała w porównaniu z objętością zajmowaną przez gaz

Równanie stanu gazu, równanie Clapeyrona.

Założenia kinetycznej teorii gazu doskonałego-

-cząsteczki gazu można traktować jako punkty materialne

-znajdują się w szybkim chaotycznym ruchu

-zderzają się sprężyście ze sobą i ściankami naczynia

-siły działają tylko w momencie zderzenie

-V cząsteczek gazu jest zaniedbywalnie mała w porównaniu z objętością zajmowaną przez gaz

Ciśnienie gazu doskonałego

p = (mN-V²)/3V, przy czym p=1/3gęstość * V²

Rozkład Maxwella.

pV = (mN-V²)/3

pV=2/5NE

E=2/3kT

f(v)=[4/pierw(pi)] * [v²/v²p] * e^-v2/v2p

mam napisane jeszcze: cząsteczki kurzu wykonują ruchy, ponieważ są poruszane przez cząsteczki powietrza

Ruchy Browna nazywamy zjawisko polegające na tym, że niewielkie cząsteczki, pyłki znajdujące się w gazie, lub w zawiesinie samorzutnie i pozornie bez powodu wykonują stałe chaotyczne ruchy w różne strony. Zachowują się przy tym jak małe żyjątka, które szukają sobie czegoś w otoczeniu. Odkrycie (zaobserwowanie) tego zjawiska zawdzięczamy biologowi - Robertowi Brownowi, który też początkowo poruszające się pyłki potraktował właśnie jako małe istoty żywe.

Ciepło molowe C=cM Cp-Cr=R

Pierwsza zasada termodynamiki

∆U=Q+W
przyrost energii wewnętrznej w jakimkolwiek procesie układu zamkniętego jest równa sumie energii doprowadzonej w tym procesie do układu w wyniku wykonania pracy lub wymiany ciepła

Praca sił ciśnienia

dW= -Fdx- -psdx

dw= -pdW

dV<0 dodatnia praca sił

dV>0praca ujemna

Ciepło przemiany Qp=ml

Ciepło Q=mc (delat)T c-ciepło właściwe

Energia wewnętrzna. Zasada ekwipartycji energii

Przez energie wewnętrzną u danego ciała rozumiemy siłe en. Kinetycznych, ruchu cieplnego cząsteczek i en. Potencjalnych ich wzajemnego oddziaływania. Ciepło jest sposobem przekazywania energii w nie mechaniczny sposób 1 cal = 4,186J

Energia wewnętrzna, dzieli się równomiernie na wszystkie cząsteczki.

Zasada ekwipartycji energii:

Przez liczbę stopni swobody jakiegoś ciała rozumiemy liczbę zmiennych niezależnych charakteryzujących położenie ciała w przestrzeni.

Cząsteczki:

- jednoatomowe - 3 stopnie swobody

-dwuatomowe - 5 stopni swobody

-Trójatomowe - 6 stopni swobody

Silniki cieplne

Silniki cieplne to urządzenia pozwalające na zamiane ciepła na pracę

Druga zasada termodynamiki

W układzie termodynamicznie izolowanym w dowolnym procesie entropia nigdy nie maleje

Gazy rzeczywiste. Równanie van der Vaalsa.

Oznacza każdą substancje w stanie gazowym. W warunkach niskiego ciśnienia i malej gęstości ( duże odległości międzycząsteczkowe oraz dostatecznie wysokiej temperatury (znacznie powyżej punktu krytycznego gaz rzeczywisty zachowuje się podobnie do gazu doskonałego

Równanie Van der Vaalsa:

Najczęściej podawane jest dla objętości molowej gazu (dla 1 mola gazu, V = V_m):

Gdzie:

a - stała charakterystyczna dla danego gazu, uwzględniająca oddziaływanie między cząsteczkami gazu (cząsteczki gazu przyciągają się, w wyniku czego rzeczywiste ciśnienie gazu na ścianki naczynia jest mniejsze niż w przypadku, gdyby tego oddziaływania nie było),

b - stała charakterystyczna dla danego gazu, uwzględniająca skończone rozmiary cząsteczek, ma wymiar objętości, przez co uznawana jest za objętość mola cząsteczek gazu,

p - ciśnienie,

V_m = V/n - objętość molowa,

V - objętość

n - liczność (ilość gazu) w molach

T - Temperatura bezwzględna,

R - uniwersalna stała gazowa

---