0000017 (18)

Rozwiązania należało szukać na gruncie mechaniki kwantowej. Rozwinięcie tej teorii wykracza poza ramy tego podręcznika. Możemy tu podać tylko pewne przybliżone idee i wyniki. Ruch elektronu w polu kulombowskim jądra ma być opisany za pomocą fali de Broglie’a. Fale te interferują i znoszą się w miejscach, gdzie spotykają się z fazami niezgodnymi, a wzmacniają tworząc fale stojące, stacjonarne w miejscach, gdzie spotykają się z fazami zgodnymi (ryc. 1.6). Warunek stacjonamości jest spełniony, jeżeli dłu-

Orbita niedozwolona wskutek

Rvc. 1.6. Powstawanie stanów stacjonarnych według falowej interpretacji ruchu elektronu.

gość fali a zmieści się całkowitą liczbę razy w obwodzie koła o promieniu r, czyli spełniona jest zależność

Promień r oznacza odległość od jądra, dla której amplituda fali nie jest zerem. W odległości tej może się znajdować elektron. Nie trudno zauważyć, że równość 1.21, przy uwzględnieniu zależności 1.5, daje postulat Bohra (1.11). Zwróćmy jednak uwagę, że to co było założeniem u Bohra jest wnioskiem w teorii falowej. Ten nowy „falowy” model atomu daje te same stany elektronowe co teoria Bohra; także na enćrgię elektronu otrzymuje się identyczny wzór (1.14). Energia elektronu jest skwantowana. Poziom energetyczny

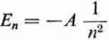
jest określony główną liczbą kwantową w = 1,2 ...

Taki falowy model atomu jest jednak dużym uproszczeniem. Mechanika kwantowa daje rozwiązania o wiele ogólniejsze.

Punktem wyjścia mechaniki falowej jest równanie Schródingera, uzyskane na podstawie dualizmu falowo-korpuskulamego materii. Równanie to pozwala znaleźć amplitudę fali de Broglie’a <J;(x,    z), zwaną funkcją falową, która opisuje stan cząstki. Kwa

drat amplitudy, inaczej funkcji falowej (ściślej kwadrat jej modułu |ó|'-), określa prawdopodobieństwo znajdowania się cząstki w jednostce objętości danego obszaru przestrzeni. Obliczając t]/² dla elektronu poruszającego się w polu kulombowskim jądra można określić prawdopodobieństwo P(r) znajdowania się elektronu w odległości r od

23