0285

286

IV. Badanie funkcji za pomocą pochodnych

Ponieważ w przypadkach I i II (III i IV) mamy do czynienia z funkcją wypukłą na dół (do góry), krzywa MM' leży pod (nad) cięciwą MM’, tj.

(4)

f(x) <f{a) +

(»

fb)-f(a) b — a

(x-a)

(a<x<b) .

Przyjmując tu x—x_v otrzymujemy bezpośrednio

f(x i)<0    (>0),

a więc f{x,) ma znak zawsze przeciwny do znaku/"(x). Wyciągamy stąd wreszcie wniosek, że w przypadkach I i IV wartość x_t leży między a i i, a w przypadkach II i III — między {i b.

Ograniczając się dalej do przypadków I i IV zastosujemy znowu naszą regułę, tym razem do przedziału <jci , b~). Zastępując w (2) a przez *i, otrzymamy nową wartość przybliżoną pierwiastka (:

x₂=x_t

{b-x_i)f(x_i)

/(&)-/(*.) zawartą na mocy powyższego między x_t a f. Proces ten można kontynuować bez końca i zbudować rosnący ciąg wartości przybliżonych

Przy tym dowolne dwie kolejne wartości x„ i x_n+t są związane wzorem

(5)

*!>+!=*»

(b-x_n)f(x„)

/(*)-/(*.) ’ analogicznym do wzoru (2).

Wykażemy, że ze wzrostem n ciąg *„->£. Rzeczywiście, zmienna x„ rosnąca i ograniczona (na przykład liczbą () musi dążyć do pewnej granicy skończonej a<<f. Jeśli przejdziemy do granicy w równości (5), wykorzystując przy tym ciągłość funkcji f(x), to otrzymamy

(b-a)f(a)

/(*)-/(«) ” ’

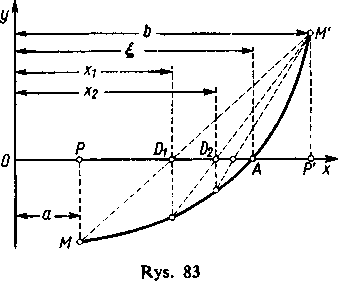
skąd/(a) = 0. Ponieważ równanie (1) nie ma w przedziale <a, ó> innych pierwiastków niż i, jest a={(')• Rysunek 83 ilustruje stopniowe przybliżanie się punktów przecięcia D_t,D₂,... kolejnych siecznych z osią x do szukanego punktu A.

Łatwo zrozumieć, że w przypadkach II lub III kolejne stosowanie reguły doprowadzi do ciągu malejącego wartości przybliżonych

b>Xi>xi> ...>x„>x_n+!>...><;

dążącego do pierwiastka ( z prawej strony.

W ten sposób we wszystkich przypadkach stosując dostatecznie wiele razy powyższą regułę można obliczyć pierwiastek ( z dowolną dokładnością. Poza tym pozostaje zresztą otwarte zagadnienie, jak oszacować dokładność obliczonej już wartości przybliżonej x_n.

(’) Zbieżność procesu można otrzymać także bez założenia dotyczącego drugiej pochodnej, wówczas jednak nie jest wykluczona możliwość, że punkty x_n przechodzą z jednej strony pierwiastka na drugą.