0261

262

IV. Badanie funkcji za pomocą pochodnych

4) Druga pochodna funkcji jc' (w tym samym przedziale) jest równa r(r — \)x'~², widać stąd, że dla r>l i r<0 funkcja ta jest wypukła, a dla 0<r<l — wklęsłaf¹); itd.

We wszystkich tych przykładach mieliśmy ścisłą wypukłość albo wklęsłość.

Na zakończenie wskażemy jeszcze jedną ważną charakterystykę geometryczną funkcji wypukłej f(x). Zamiast cięciwy wykresu funkcji y=f(x), którą rozpatrywaliśmy w ustępie 141, rozpatrzmy tu styczną w dowolnym punkcie wykresu (rys. 73).

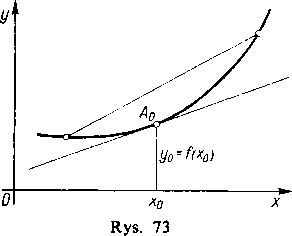
Twierdzenie 3. Niech funkcja f(x) określona i ciągła w przedziale 3C ma w tym przedziale pochodną skończoną f’(x). Na to, by f(x) była wypukła, potrzeba i wystarcza, żeby wykres jej leżał całkowicie nad dowolną styczną (lub na tej stycznej).

Konieczność. Styczna do krzywej y=f(x) w punkcie A_sfx₀,f(x₀j) ma współczynnik kątowy /'(*«,)• Równanie stycznej można zapisać w następujący sposób:

y =/Oo) +/'(* o) (x - x₀).

Trzeba wykazać, że wypukłość funkcji f(x) pociąga za sobą dla dowolnych punktów x₀ i x z 9C nierówność

(10)    f(x)>f(x₀)+f\x o)(x-x₀).

Nierówność ta jest równoważna z dwiema nierównościami

,,, x    ,,, ,J(x)-f(Xo)    ,,

(1 la)    / (x₀X- dla    x>x₀

X — x₀

i

(1 lb)    / (x₀)^- dla    x<x₀,

x-x₀

te zaś nierówności pokrywają się odpowiednio z nierównościami (7a) i (7b) otrzymanymi przy dowodzie twierdzenia 1 (właśnie przy założeniu wypukłości funkcji), jeśli w pierwszej z nich przyjąć x₂ = x, x₁=x₀, a w drugiej x₂=x₀, x_t=x.

Dostateczność. Załóżmy na odwrót, że spełniona jest nierówność (10) lub, co na jedno wychodzi, nierówności (1 la) i (1 lb). Wówczas można z nich odtworzyć nierówności (7a) i (7b), skąd wynika, że f'(x₁)^f'(x₂), a więc pochodna f{x) jest funkcją rosnącą. To zaś, jak wiemy (twierdzenie 1), pociąga za sobą z kolei wypukłość funkcji / (x).

Uwaga. Zwracamy uwagę czytelnika na to, że faktycznie (patrz odsyłacz na str. 261) konieczność nierówności (10) dla danego x₀ i dowolnego x/x₀ została udowodniona przy założeniu istnienia pochodnej f'(x₀) tylko w samym punkcie x₀.

O Przykład ten pozwala przy sposobności pokazać, że iloczyn dwóch funkcji wypukłych może nie być funkcją wypukłą. Tak więc funkcja —x¹¹³ jest wypukła, podczas gdy jej kwadrat, tzn. funkcja x^2/3 jest wklęsła.