0243

244

IV. Badanie funkcji za pomocą pochodnych

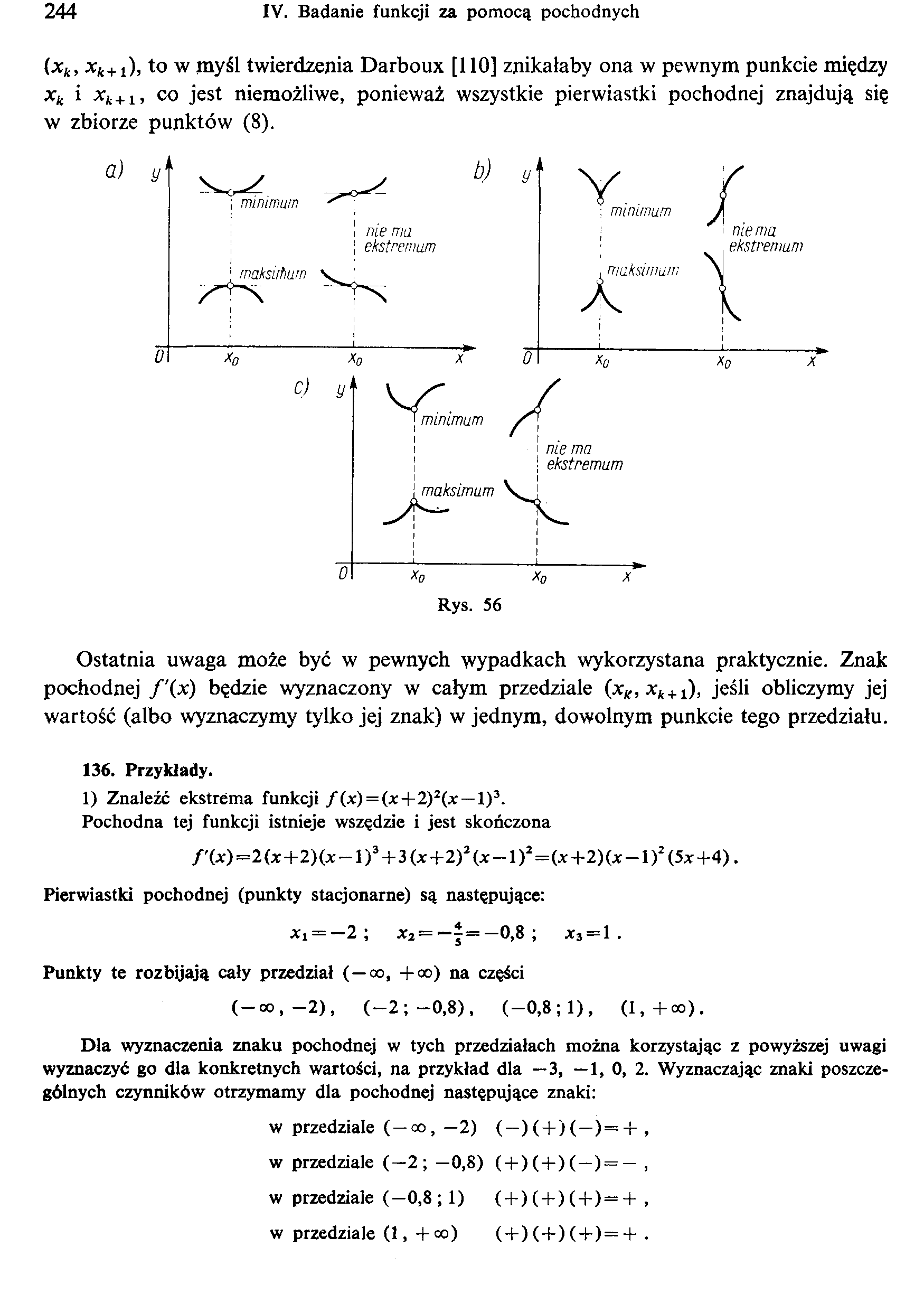
(x_k, jc*₊₁), to w myśl twierdzenia Darboux [110] znikałaby ona w pewnym punkcie między x_k i x_{k + 1}, co jest niemożliwe, ponieważ wszystkie pierwiastki pochodnej znajdują się w zbiorze punktów (8).

a)

y

0

me ma ekstremum

maksirtium

b)

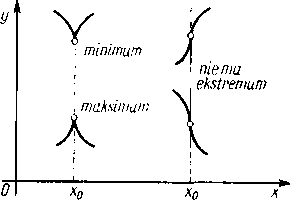
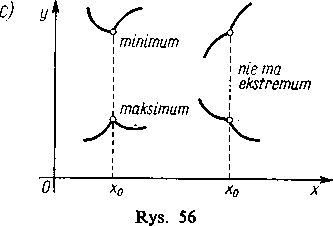
Ostatnia uwaga może być w pewnych wypadkach wykorzystana praktycznie. Znak pochodnej f'(x) będzie wyznaczony w całym przedziale (x_k, x^₊₁), jeśli obliczymy jej wartość (albo wyznaczymy tylko jej znak) w jednym, dowolnym punkcie tego przedziału.

136. Przykłady.

1) Znaleźć ekstrema funkcji f(x) = (x+2)²(x —l)³.

Pochodna tej funkcji istnieje wszędzie i jest skończona

y"(AT)=2(je+2)(jc —1)³ + 3(jc+2)²(^t —1)²=(jc+2)(jc —l)² (5je+4).

Pierwiastki pochodnej (punkty stacjonarne) są następujące:

xi = — 2;    *2 = — f=— 0,8;    *₃ = 1 .

Punkty te rozbijają cały przedział (—co, +oo) na części

(-oo,-2),    (-2; -0,8),    (-0,8 ;1),    (l,+oo).

Dla wyznaczenia znaku pochodnej w tych przedziałach można korzystając z powyższej uwagi wyznaczyć go dla konkretnych wartości, na przykład dla —3, —1, 0, 2. Wyznaczając znaki poszczególnych czynników otrzymamy dla pochodnej następujące znaki:

w przedziale (-co,-2) (-)(+)(-)=+,

w przedziale (—2; —0,8) ( + )(+)(—)=— ,

w przedziale (-0,8 ; 1)    (+)( + )(+)=+,

w przedziale (1,+oo)    (+)(+)(+)=+.