0259

260

IV. Badanie funkcji za pomocą pochodnych

siałaby osiągać wewnątrz tego przedziału, co dla funkcji wypukłej różnej od stałej jest niemożliwe (patrz 5°). Tak więc wewnątrz przedziału jest f(x)<l(x), krzywa leży pod cięciwą i zależność (1) jest spełniona zawsze ze znakiem nierówności.

Jeśli dla dowolnego przedziału (x₂, x₂}, gdzie x₂<x₂, zawartego w SC zależność (1) jest spełniona ze znakiem nierówności, to funkcję f(x) nazywamy ściśle wypukłą. Analogicznie wprowadzamy pojęcie funkcji ściśle wklęsłej. Terminologię tę stosujemy jednocześnie również do krzywej y=f{x).

143. Warunki wypukłości funkcji. Biorąc pod uwagę (2) i (2a) możemy zapisać podsta wową nierówność (1) w postaci

x₂— x    x — x,

f(x)ś--f(x₁)+-f(x₂)

X₂-X i    X₂-X_i

lub symetryczniej

(4)    (x₂ - x)f(x!) + (*! - x₂)f( x) + (x - x i )/(x₂) ^ 0.

Warunek ten można wreszcie napisać za pomocą wyznacznika w postaci

(5)

1

1

*i

x

^X2

/(* l)

f(x)

/(*₂)

5*0.

We wszystkich przypadkach zakładamy, że x jest zawarte między x_t a x₂; dla ustalenia uwagi będziemy odtąd zakładali, że x_t <x₂.

Zwracamy przy sposobności uwagę na to, że warunek wypukłości funkcji w postaci (5)

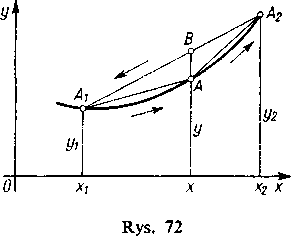
ma bezpośrednią interpretację geometryczną, jeśli przypomnimy sobie, że napisany wyznacznik wyraża podwójne pole trójkąta A₂AA₂ (rys. 72) ze znakiem plus właśnie wówczas, gdy trójkąt jest dodatnio zorientowany, tzn. jego obwód A_x-A-— A₂ jest obiegany w kierunku przeciwnym do ruchu wskazówki zegara.

Zaznaczamy specjalnie, że gdy chodzi o ścisłą wypukłość, we wszystkich tych warunkach znak równości powinien być wyłączony.

Wygodne do sprawdzenia warunki wypukłości otrzymujemy posługując się pochodnymi funkcji. Twierdzenie 1. Niech funkcja f (x) określona i ciągła w przedziale SI ma w tym przedziale pochodną skończoną f'{x). Na to, by funkcja f (x) była wypukła w SC, potrzeba i wystarcza, by jej pochodna f'(x) była rosnąca (w szerszym sensie, tzn. słabo rosnąca).

Konieczność. Niech funkcja f{x) będzie wypukła. Zakładając, że x₁<x<x₂, napiszemy warunek (4) w postaci

^    f(x)-f{x₁) f(x₂)-f(x)

(6) - ---.

X — X_t    X₂ — X