1 M3 PaprzyckiG WojtkoK ZAD17

P/2

dx

T =

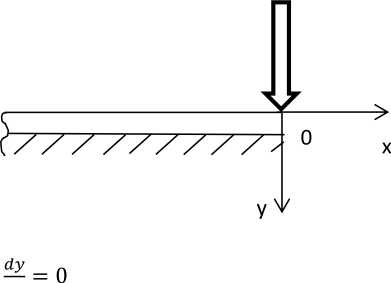
b) Rozważmy lewą część belki:

5) Warunki brzegowe:

a.    Dla x=0,

b.    Dla x=0,

6) Całka ogólna rozwiązania równania różniczkowego ma postać:

y = e^ax(Acosax + Bsinax) + e~^ax{Ccosax + Dsinax) Biorąc pod uwagę, że

y=0 oraz — = 0

dx

dla x->-°°,

zatem A=0 oraz B=0.

Wówczas:

y = e ^ax(Ccosax + Dsinax)

7) Obliczmy pochodne:

dy

— = — ae ^ax((C — D)cosax + (C + D)sinax) dx

d²y dx²

— 2a³ e~^ax ((D — C)sinax + (C + D)cosax)

— 2 a²e~^ax(Csinax — Dcosax)

d³y

dx³

8) Obliczenie stałych całkowania na podstawie warunków brzegowych:

Z 1. warunku brzegowego:

0 = — ae~^a'°((C — D)cosa ■ 0 + (C + D)sina ■ 0) (C-D) = 0 C = D