0000062 (3)

w cieczy. Wpływa to na zmianę wartości współczynnika lepkości rj, który zależy wówczas od wielkości gradientu. Ciecze, dla których współczynnik r\ nie jest wielkością stałą, nazywamy cieczami nienewtonowskimi.

Opisana powyżej orientacja asymetrycznych makrocząsteczek w cieczach o dużym gradiencie prędkości przejawia się również we właściwościach optycznych takich roztworów. Stają się one dwójłomne, tak jak niektóre kryształy, choć w mniejszym stopniu. Zjawisko to nazywamy dwójłomnością prądową. Ilościowe pomiary takiej dwójiomności dają również informacje o kształcie makrocząsteczek.

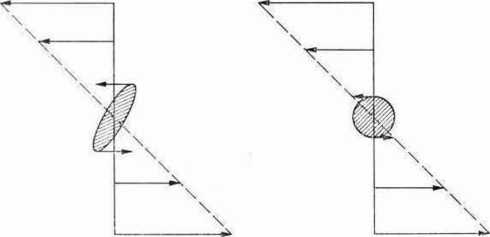
Ryc. 8.11. Pary sił działające na makrocząsteczki o różnych kształtach w gradiencie prędkości cieczy.

Dyfuzja makrocząsteczek w roztworze. Współczynnik dyfuzji D (rozdz. 5.2.1) zależy między innymi od rozmiarów i kształtów cząsteczek dyfundujących. Z pomiarów współczynnika dyfuzji można więc wnosić o cechach charakteryzujących makrocząsteczki. Przykładowo, dla cząsteczek kulistych zależność współczynnika dyfuzji od promienia r cząsteczki wyraża się wzorem

6-nrjr

gdzie i) oznacza lepkość rozpuszczalnika.

Wzór 8.1 można otrzymać następująco. Przemieszczenie 1 mola substancji z miejsca o stężeniu c do miejsca o stężeniu c—dc (ryc. 5.2) wymaga wykonania pracy równej zmianie potencjału chemicznego, która zgodnie z 4.31 wynosi

c    dc ¹

d(z = RT In- = RT-    8.2

c—dc    c

dx

Dyfundujące cząsteczki napotykają na opór F, proporcjonalny do ich prędkości v = -, czyli

dr

8.3

dx

F = fv albo F = /-

dr

Współczynnik oporu/zależy od rozmiarów i kształtu cząsteczek oraz od lepkości nj rozpuszczalnika.

162

1

Skorzystano z zależności In (1—x) S —x, dla jc <§ 1.