1

Dla 1 mola gazu doskonałego (jednotomowego) N =    pV = RT,

stąd

| (O - RT ■ KNJ 1

(^E>)

n_a

r;n_a = k

- <^ek>*f^kT

⁼ <^ek>

dla, 1 czu,{tti

dla- n hnoU

dl Cu <Ł hnola-

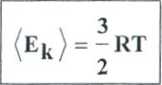
(stała Bolzmanna)

k

(e*>

k = 138-to'" J/K

/£ v ^ fcT¹ u jeJr ió energta, Cki'*>etynio*)

**■ '    2.    HZi/nę.ł-fZna, —?* SpecjcJnt, O?no-

•z 4?_fc z&u ru^T tisną

Równanie stanu gazu (Clapeyrona)

ok. 1834 r.

pon* tz-*-jqce-fo /i-t ^

jo-l-Oft prfJkoito*} C

n V    J

- - -- = 8,314-= R (uniwersalna stała gazowa)

T_n    K • mol

pV = RT (dla 1 mola)

pV = n RT (dla n moli)

Jest to równanie empiryczne

• dla stałej T -»

•    dla stałego p -»

•    dla stałej V -»

W w/w przypadkach

pV = const

V

— = const T

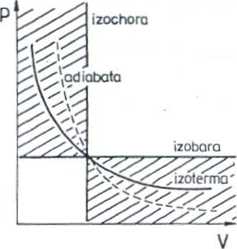
przemiana izotermiczna (prawo Boyle’a - Mariotte’a)

1662 r. 1676 r.

przemiana izobaryczna (prawo Gay - Lussaca)

1802 r.

p

— = const

T

przemiana izochoryczna (prawo Charlesa) _{1?8g p} zachodzi wymiana ciepła z otoczeniem

przemiana adiabatyczna - bez wymiany ciepła z otoczeniem

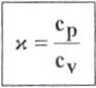
pV^x = const

dla tej przemiany też obowiązuje równanie stanu

a)    b)

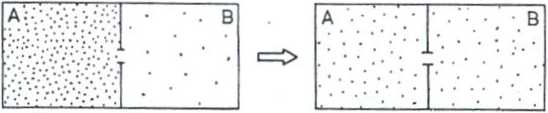
Ta * "(b . Pa * Pb    Ta = T_b , p_A = p_B

Pa* Pb    Ha= Pb

•> dQ = C ■ m • dT = C • lip. -dT ; C- ciepło właściwe - miara pojemności cieplnej substancji; p - masa jednego mola

- dla cieczy c większe niż dla ciał stałych (np. dla wody ok. 6,5 x większe niż dla stali);

- dla gazów c_p > c_v (c_p - przy p = const, c_v - przy V = const)

Cp JA ^1 Cp

Cu- JA. — c„

Cp - c„ + R

Rys.    Podukłady A i B: a) przed i b) po osiągnięciu stanu równowagi

termodynamicznej

1

Równowaga termodynamiczna - stan, do którego dążą wszystkie układy izolowane; nie ma w nim zmian makroskopowych

przemiana termodynamiczna równowagowa (ideaIizacja)-» układ nieskończenie (bardzo) powoli przechodzi przez kolejne stany równowagi od punktu P do punktu K; inaczej - guasistatyczna.

-    procesy ąuasistatyczne są równocześnie odwracalne (przy braku dysypacji energii)

-    termodynamika fenomenologiczna - równowagowa (tą się zajmujemy)

- nierównowagowa