3

Doświadczalne wyznaczanie środka iii poprzecznych odbywać się będzie przez pomiar ugięcia dowolnego punktu C lezącego na osi z (rys. 4.63a) a tnkżc ugięcia punktu O leżącego na rur/e na osi y. Punkty te doznają przemieszczeń wywołanych zginaniem:

(4.163)
gdzie: IJ - x • r1 • 3 - moment bezwładności przekroju rury [mm'1], oraz, jeżeli siła P będ/jc
poza środkiem sil poprzecznych (w odległości c [mm] od tego środka), przemieszczeń wywołanych skręcaniem. Przyjmując założenie, żc skręcanie jest skręcaniem swobodnym wzór na te przemieszczenia przybierze (przykładowo dla punktu C) postać:
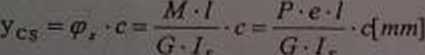
(4.164)
gdzie: M = P- e - moment zewnętrzny skręcający pret (rys. 4.63b), cp, - kąt skręcenia swobodnego [rd], zaś:
Is - sztywność geometryczna skręcania pręta [mm*],
E, G - moduły materiału odpowiednio sprężystości wzdłużnej i postaciowej [MPa], c - odległość punktu pomiarowego od środka sił poprzecznych (ścinania) |mm] (na rysunku zaznaczono tę odległość od punktu C).
Całkowite przemieszczenie przykładowo punktu C wyniesie więc:
(4.165)
yc=ys+)'cs
Zmieniając położenie siły P względem środka sił poprzecznych uzyska się wykresy przemieszczeń punktu C i punktu O w funkcji położeń siły P jak pokazuje rys. 4.64. Przecięcie się tych wykresów wyznacza położenie środka sił poprzecznych co pokazano na rysunku.Na rysunku zaznaczono prostą poziomą wyznaczoną wartością ys = yo (również ustaloną doświadczalnie przez pomiur ugięcia punktu S - rys. 4.62 -teoretycznie ustalonego środka ścinania)
Opisany modę! dotyczy przypadku skręcania swobodnego tzn takiego przy którym zachodzi swobodna dcplanacja (paczeme) przekroju poprzecznego rury. Polega to na tym, żc punkty przekroju poprzecznego doznają przemieszczeń w kierunku wzdłużnym czyli równoległym do osi rury. Szczególnie jest to ważne dla profili cienkościennych otwartych czyli takich jak rozpatrywany w ćwiczeniu. Jeżeli laka dcplanacja zachodzi to w przekroju poprzecznym rury niema innych naprężeń poza opisanymi powyżej Warunkiem swobodnej dcplnnacji jest właściwe podparcie tzn mc blokujące ruchów wzdłużnych punktów
Wyszukiwarka
Podobne podstrony:
Doświadczalne wyznaczanie środka iii poprzecznych odbywać się będzie przez pomiar ugięcia dowolnego
Doświadczalne wyznaczanie środka iii poprzecznych odbywać się będzie przez pomiar ugięcia dowolnego
Doświadczalne wyznaczanie środka iii poprzecznych odbywać się będzie przez pomiar ugięcia dowolnego
Odpowietrzenie grzejników w miarę potrzeby odbywać się będzie poprzez odpowietrzniki ręczne stanowią
page0380 •> 7 381; ś ą g}u s t III. trybunału odbywanie się i domagała się od k
IMGp28 (2) pomieszczenie, w którym odbywać się będzie rozmowa oraz życzliwość, uśmiech, cierpliwość
4 sali kinowej odbywać się będzie za pomocą wyłączników z sygnalizacją świetlną zlokalizowanych w
7.SPOSOBY INFORMOWANIA RODZICÓW O POSTĘPACH DZIECKA. Informowanie rodziców o uczniu odbywać się będz
przedmiotów ogóinokształcqcych dla wszystkich szczebli szkolnictwa odbywać się będzie w systemie stu
1.16 Zasilanie energetyczne obiektów oczyszczalni Zasilanie oczyszczalni odbywać się będzie zaliczni
Etapy przeprowadzenia naboru: Nabór do służby odbywać się będzie w czterech etapach. 1.
Wyznaczenie krzywej czynników dyskontowych odbywa się przez dopasowanie krzywej czynników dyskontowy
Po podpisaniu porozumienia przez dyrektora placówki, w której odbywać się będzie praktyka, obydwa
dr inż. Jan I .cwińsjci dr inz Robert Lindcmann 4.9. Doświadczalne wyznaczanie środka sil
więcej podobnych podstron