CCF20091202036

średnią, tym większe będą liczby w obu składnikach wyrażenia podpier-wiastkowego, chociaż wynik ostateczny będzie zawsze prawidłowy.

Wzór ten można jeszcze dalej zmodyfikować wprowadzając liczbę przedziałów, d[ jako jednostkę odległości. Podobnie jak w rozdziale 5, wyłączamy szerokość przedziału z każdej waitości d, i mnożymy przez i wynik ostatecznie otrzymany z obliczeń. Wzór obliczeniowy przybiera więc postać

ifdf

5

Czyli

N

k

1/ /= 1

N

s — i

■A Y 1	! i* ifyp i—i
/ -V	N
E/rf* i i— i	(H
^1 1 N	i»/
1 k Z i-l	d wy /=i
	N
N

(6.10)

(6.11)

(6.12)

i— 1

Zauważmy, że w rezultacie wyciągnęliśmy tylko szerokość przedziału, i, poza pierwiastek.

Tabela 6.1. Obliczenie odchylenia standardowego z danych pogrupowanych

Dokładne granice przedziałów	Punkty środkowe przedziałów	f*	d'i		fid?
1950-2950	2450	17	-3	-51	i53
2950-3950	3450	26	-2	-52	104
3950-4950	4450	38	-1	-38	38
4950-5950	5450	51	0	0	0
5950-6950	6450	36	1	36	36
6950-7950	7450	21	2	42	84
Razem		189		-63	415

= 1000

415

189

= 1000 j/2,196-0,111

= 1444

Obliczając odchylenie standardowe z danych pogrupowanych rozszerzamy tabelę obliczeniową dla średniej o kolumnę Można obliczać wartości d'² i mnożyć je przez /„ prościej jednak jest pomnożyć dwie ostatnie kolumny stosowane przy obliczaniu średniej (tj. d'_t Xf_id'_i). Mnożymy iloczyn d[ przez siebie i widzimy, że wszystkie znaki ujemne przekształciły się w dodatnie. W tabeli 6.1 przeprowadzamy obliczenie dla danych z poprzedniego rozdziału. Dla zilustrowania tego problemu posługujemy się wzorem (6.10), chociaż wzór (6.12) daje mniejsze błędy zaokrągleń.

Wiemy więc już, że średni dochód wynosi 5117 dok, a odchylenie standardowe 1444 doi. Liczb tych możemy używać jako streszczenia danych empirycznych lub do porównywania z inną próbą. Przekonamy się dalej, że są one także potrzebne przy testowaniu hipotez i przy oszacowywaniu wartości mierników w populacji.

6.5. WSPÓŁCZYNNIK ZMIENNOŚCI

Czasem chcemy porównać pod względem jednorodności kilka grup o bardzo różniących się między sobą średnich. Porównywanie wielkości odchyleń standardowych może być w takich przypadkach nieco mylące. Można się bowiem spodziewać, że próby o dużych wartościach średniej będą też miały stosunkowo duże odchylenie standardowe. Powinniśmy się raczej interesować wielkością odchylenia standardowego w stosunku do średniej. Oznacza to, że miernik względnej zmienności można otrzymać dzieląc odchylenie standardowe przez średnią. Iloraz ten nazywa się współczynnikiem zmienności; oznaczamy go literą V. Tak więc

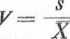
89