czwornik2

dla pracy odwrotnej czwórnika (rys. 2)

I

1

1

O

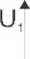
2

O

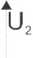
O

2

gdyż dla rozważanego czwórnika det[a] 1.

2. Im podanej a wejściowa czwórnika określona jest związkiem:

₂ __z _u_{1 =} au_{2 +} bi₂ "^r 1    /, cu₂ + di₂

3.

~u;		D	B'	~u;
_i2		C	A

Stany pracy czwórnika.

W różnych stanach pracy czwórnika impedancja wejściowa wynosi:

A

C

B

D

a)    stan jałowy (12=0): Z_l0 =

b)    stan zwarcia (IJ2=0): Z_|z =

c) stan jałowy - praca odwrotna czwórnika (1|=0):

Z

20

D

C

ł.ącząc powyższe związki można znaleźć elementy macierzy łańcuchowej od impedancji w stanie jałowym i zwarcia:

C

(Z\o —Z,_z)Z₂

D = CZ₂₀, A = CZ_io, B = DZ_V/

20

4. Obciążenie charakterystyczne (falowe) czwórnika.

Gdy impedancja obciążenia czwórnika równa jest impedancji falowej, wówczas impedancja wejściowa tego czwórnika równa się także impedancji falowej (charakterystycznej).

Impedancję falową można uzależnić od elementów macierzy łańcuchowej:

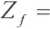
A-D±

(D-A)² -4BC 2 C