fiza1

R. Krupa

18.

WYZNACZANIE POJEMNOŚCI KONDENSATORA METODĄ POMIARU CZASU ROZŁADOWANIA

18.1. Wprowadzenie

W pomiarach pojemności kondensatorów powszechnie stosuje się różnego rodzaju mostki prądu przemiennego. Istnieją jednak pewne typy kondensatorów (np. kondensatory elektrolityczne), których polamość nie pozwala na włączenie w obwód mostka prądu zmiennego. Pojemność tego typu kondensatorów wyznacza się innymi metodami. Jedna z nich polega na pomiarze czasu rozładowania kondensatora. W metodzie tej wykorzystuje się równanie krzywej rozładowania kondensatora.

Załóżmy, że kondensator o pojemności C został naładowany do napięcia U₀. W chwili t = 0 okładki kondensatora zostały zwarte opornikiem o stałym oporze R (rys. 18.1). Poprzez opór ten popłynie prąd o stopniowo malejącym natężeniu /, powodując rozładowanie kondensatora. Zgodnie z prawem Ohma natężenie / prądu rozładowania kondensatora w dowolnej chwili t wynosi

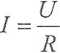
(18.1)

gdzie:

U- napięcie między okładkami kondensatora w chwili t.

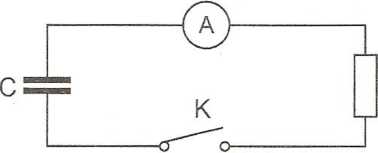
Rys. 18.1

Przepływ prądu o natężeniu / spowoduje przeniesienie w ciągu czasu dt ładunku dQ - Idt. O ten właśnie ładunek dQ maleje ładunek kondensatora. Zatem ubytek ładunku kondensatora wyniesie

(18.2)

- dQ - Idt = —dt R

W oparciu o definicję pojemności kondensatora, zgromadzony na nim ładunek można określić wzorem:

(18.3)

Q - CU

Różniczkując zależność (18.3) otrzymamy

Ćwiczenia laboratoryjne z fizyki 119