fiza2

WYZNACZANIE POJEMNOŚCI KONDENSATORA...

	dQ = CdU	(18.4)
Porównując prawe strony zależności (18.2) i (18.4) otrzymujemy
stąd	—dt- -CdU R dU dt	(18.5)
	U ~ CR	(18.6)
Całkując lewą stronę ostatniego równania w granicach od Uo do U i granicach od 0 do / otrzymujemy . U 1		prawą stronę w
	In— =--1 U0 CR	(18.7)
a więc
lub	U = U0e^CR r, r, TO	(18.8)
	^u = u^\-cr)	(18.8a)

gdzie:

e - podstawa logarytmu naturalnego.

Podstawiając otrzymany wynik do prawa Ohma (18.1) otrzymamy więc

I = I₀e^CR    (18.9)

lub

I = I₀ exp

_t_\ CR j

(18.9a)

Zatem zarówno napięcie na kondensatorze, jak i natężenie prądu rozładowania maleje w trakcie rozładowania kondensatora wg krzywej wykładniczej.

Jeżeli zmierzymy czas rozładowania t₀ kondensatora o znanej pojemności C₀, a następnie nie zmieniając parametrów układu, zmierzymy czas rozładowania kondensatora o nieznanej pojemności C_x, to wykorzystując wyprowadzony uprzednio wzór (18.8) opisujący zależność napięcia na kondensatorze od czasu rozładowania możemy napisać:

U_z = U₀ exp

RC,

Oj

(18.10)

^U, = ^Uo ^exP

f

K

\

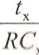
i

(18.11)

gdzie:

U_t) napięcie żródln ładowania kondcnsaloia

O, napięcie na KomIciimiiIui c, pi v klórym nanlnpi /npitli nli w...... I i I i

l'oii'i\vnnji|i phiwt aliony lównnri ( I M IO)i(lH I I } nli , nm|' m .

(

exp

RC,

- exp

o

V

RC,,

(IH.I ')

skąd

Cq C_x

(18.1 ')

lub

C=C^    (18.M)

^x    O f

^lO

Wzór (18.14) pozwala obliczyć szukaną pojemność kondensatora C_x. Ze wzoru In¹,o wynika, że czas rozładowania kondensatora jest proporcjonalny do jego pojemności

t

X

c„

c„

(18 IM

18.2. Wykonanie ćwiczenia

Sprawdzenie słuszności zależności (18.14)

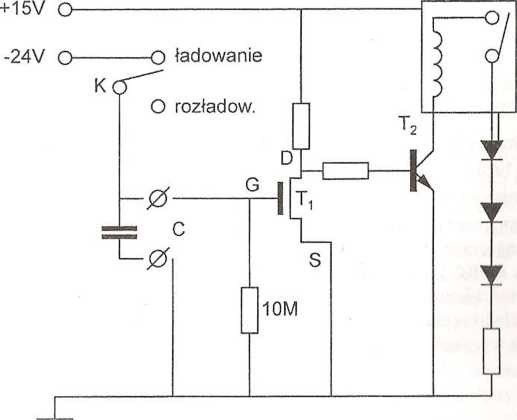
Tranzysloiy

T., - BI 245C T₂ - BDW &:k:

D - diodo nyu

Rys. 18.2. Układ elektroniczny pozwalający na pomiar czasu rozładowania koi uiom-ihun

1

Do zacisków C układu pomiarowego podłączyć kondensator A, o nieznanej po|< iii ilości.

\ Przełącznik K ustawić w pozycji „rozładowanie” i włączyć układ pomiaiowy do sieci.

IM/.cliiczyć na kilka sekund pi *• lip nil- I w pozycję „ładowanie" (diody syp,nuli, a cyjne I) świccn),

I Kównoc .'cśnic w l.p . ■ n u mi loj.. ot |,. Di, y' pi < lip , 1111 I. nn pozycji; „iozimin Wttllle"