Image040

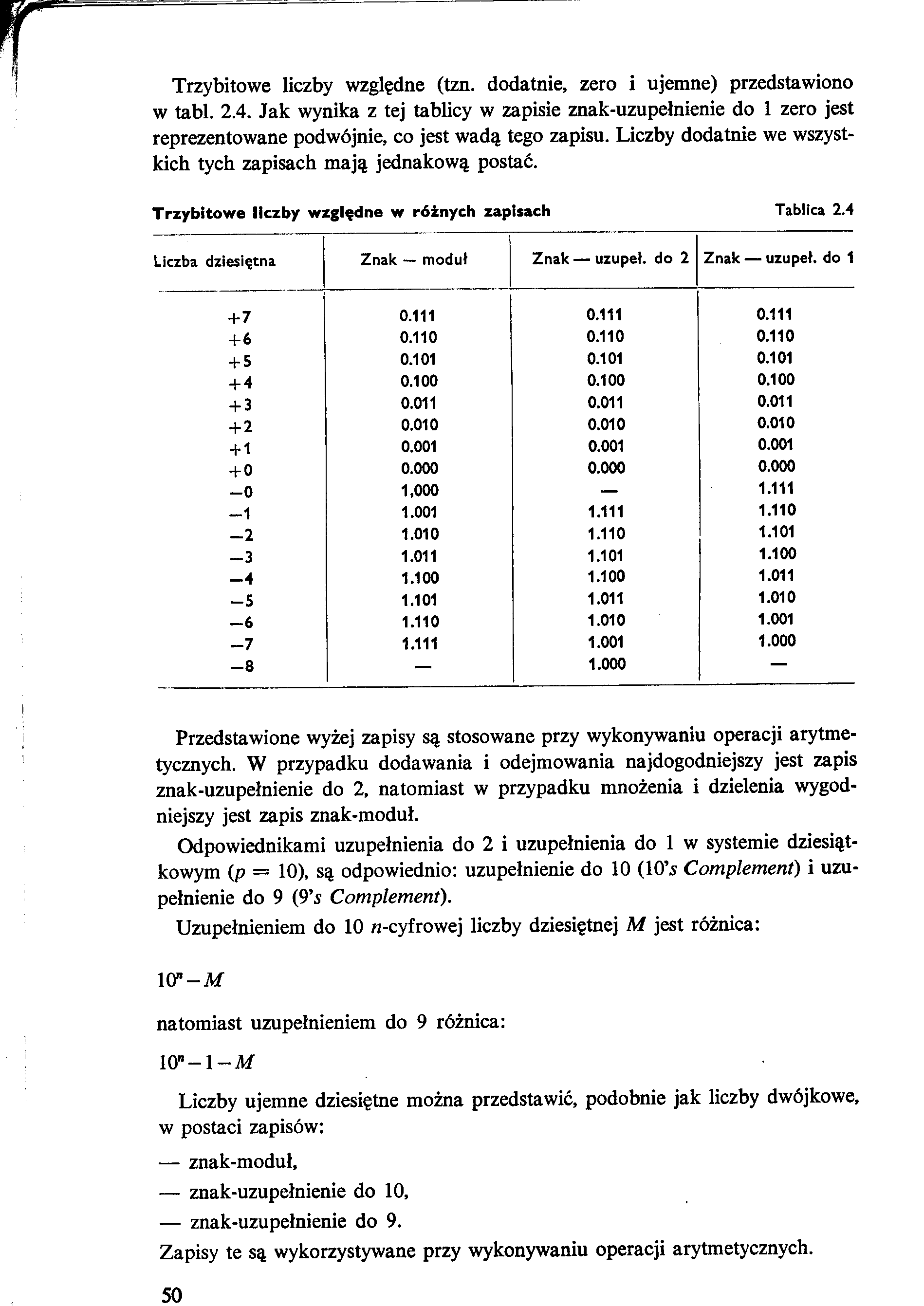
Trzybitowe liczby względne (tzn. dodatnie, zero i ujemne) przedstawiono w tabl. 2.4. Jak wynika z tej tablicy w zapisie znak-uzupełnienie do 1 zero jest reprezentowane podwójnie, co jest wadą tego zapisu. Liczby dodatnie we wszystkich tych zapisach mają jednakową postać.

Trzybitowe liczby względne w różnych zapisach    Tablica 2.4

Liczba dziesiętna	Znak — moduł	Znak — uzupeł. do 2	Znak — uzupeł. do 1
+7	0.111	0.111	0.111
+ 6	0.110	0.110	0.110
+ 5	0.101	0.101	0.101
+ 4	0.100	0.100	0.100
+ 3	0.011	0.011	0.011
+ 2	0.010	0.010	0.010
+ 1	0.001	0.001	0.001
+ 0	0.000	0.000	0.000
-0	1,000	—	1.111
-1	1.001	1.111	1.110
-2	1.010	1.110	1.101
-3	1.011	1.101	1.100
-4	1.100	1.100	1.011
-5	1.101	1.011	1.010
-6	1.110	1.010	1.001
-7	1.111	1.001	1.000
-8	—	1.000	—

Przedstawione wyżej zapisy są stosowane przy wykonywaniu operacji arytmetycznych. W przypadku dodawania i odejmowania najdogodniejszy jest zapis znak-uzupełnienie do 2, natomiast w przypadku mnożenia i dzielenia wygodniejszy jest zapis znak-moduł.

Odpowiednikami uzupełnienia do 2 i uzupełnienia do 1 w systemie dziesiątkowym {p = 10), są odpowiednio: uzupełnienie do 10 (10’s Complement) i uzupełnienie do 9 (9's Complement).

Uzupełnieniem do 10 rc-cyfrowej liczby dziesiętnej M jest różnica:

10"—M

natomiast uzupełnieniem do 9 różnica:

10"—1—Af

Liczby ujemne dziesiętne można przedstawić, podobnie jak liczby dwójkowe, w postaci zapisów:

—    znak-moduł,

—    znak-uzupełnienie do 10,

—    znak-uzupełnienie do 9.

Zapisy te są wykorzystywane przy wykonywaniu operacji arytmetycznych.

50