Image286

nienie w obrębie jednej pozycji wynosi 2A/, a dla w-pozycyjnego sumatora rozpatrywanego typu (sumatora kaskadowego) czas propagacji — dla najgorszego przypadku — wynosi 2nAf.

Rozwijając funkcje przełączające (1) i (2) otrzymamy:

—    dla najmniej znaczącej pozycji:

51 = Si Cq “ł" A-i Co -I^- Ai Bi Co -f- A.I Si Cq    (3)

Ci = Ai Bi ~ł“Ai Co ~¥Bi C₀    (4)

—    dla następnej pozycji mamy:

52    — A 2B2C1 -\rA2B2C1+A2B2 Ci +A2B2 Ci    (5)

Podstawiając wyrażenie (4-4) do wyrażenia (4-5) otrzymamy:

S2 “

+ ^2    Al Bi +A2B2 Al Co +^2 B1 Co +

Ą- A2B2A1 Bi A2B2A1 Co H- A2B2Bi Cq +

"h A2B2 Ai Bi -I^- A2 B2 Ai Co 4" A2B2 Bi Co    (6)

Z postaci wyrażenia (6) wynika, że S₂ otrzymujemy z takim samym opóźnieniem co S₁. Układ utworzony na podstawie tak rozwiniętych funkcji zwany jest sumatorem z przeniesieniami jednoczesnymi (sumator typu „look-ahead”)-Niestety funkcje takie stają się za długie w przypadkach praktycznych, gdy licz-

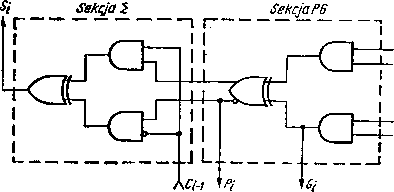
Rys. 4.326. Schemat ideowy i-tego stopnia sumatora pełnego

ba bitów sumowanych liczb zawiera się w granicach 20 -r- 60. Do realizacji wyrażenia np. 5₆₄ według przedstawionej procedury wymaganych jest prawie 10²⁰ bramek!

W celu uproszczenia przytoczonych dalej rozważań wprowadzono następujące definicje stanów jednopozycyjnego sumatora pełnego, nazywanego dalej stopniem (rys. 4.326):

— stopień i jest w stanie generacji, tzn. G_t — 1, wtedy i tylko wtedy, gdy A_t —

= *i = 1:

G_t = A_gB_ę    (7)

— stopień i jest w stanie propagacji, tzn. P_{ = 1, wtedy i tylko wtedy, gdy

P_t - At®B_t = A_tB_t+A_tB_t    (8)