img023

23

2.4. Recepcja i struktura przestrzeni cech

Składowe x„ tych wektorów chętnie będziemy traktowali jako liczby x„ 6 Tl określające ilościową miarę określonej cechy, co powoduje, że przestrzeń X traktowana będzie jako n-wymiarowa przestrzeń euklidesowa (X C Tl"). W takiej przestrzeni stosunkowo najłatwiej i w najbardziej naturalny sposób inożna będzie prowadzić wszystkie analizy i rozważania, dlatego przestrzeń ta traktowana będzie przez nas jako model standardowy.

Dla ilustracji prowadzonych rozważań przyjmować będziemy dodatkowo, że mamy do czynienia z przestrzenią dwuwymiarową (n = 2), aby można było odwzorowywać rozważane obiekty jako punkty na płaszczyźnie, zaś w niektórych przypadkach uciekać się będziemy nawet do „przestrzeni” jednowymiarowych, co oczywiście nie odpowiada na ogół rzeczywistemu zadaniu rozpoznawania, a służyć będzie głównie temu, by wygodnie zaprezentować pewne prawidłowości i współzależności na rysunku.

Przykład. Na rysunku 2.1 przedstawiono, w jaki sposób cechy obiektów wyznaczają współrzędne punktów w przestrzeni cech i jak dochodzi do odwzorowania obiektu feflw punkt z*¹ € X, charakteryzowany przez współrzędne r”

stopień ¹¹ szarości

x\

1	obiekt 1_______
	griW
o-----(pobiekt 2	* ^xi
1	pomiar cech
	/ odwzorowuje
1	/ obiekty
1 obiekt 1	^ w punkty
^<l— _ ! “?	przestrzeni
-4-4-	->•

średnica

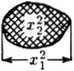
Rys. 2.1. Rozpoznawane obiekty mogą być traktowane jako punkty w przestrzeni cech. Na rysunku pokazano przestrzeń cech, w której na osi poziomej odkładana jest średnica obiektu, a na osi pionowej - jego stopień szarości

obiekt 2

j¹) Dalsze szczegóły na ten temat - patrz: Dodatek 1.