img110

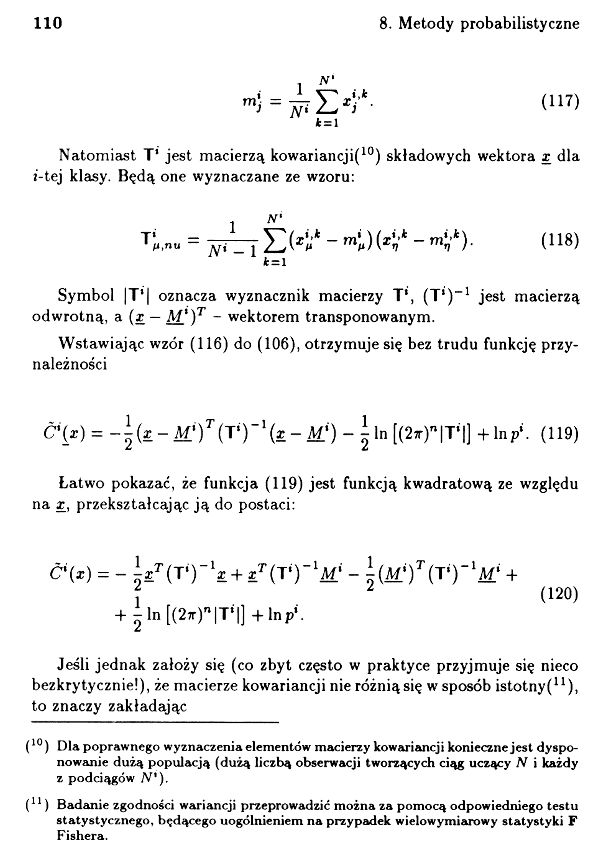
110

8. Metody probabilistyczne

(117)

1 ^N'

i ⁼ Ś ^x'i

k = 1

Natomiast T* jest macierzą kowariancji(¹⁰) składowych wektora x dla i-tej klasy. Będą one wyznaczane ze wzoru:

T‘

= vrriD*i^ł-^m5‘) (<•*-<)■

fc=l

(118)

Symbol |T‘| oznacza wyznacznik macierzy T¹, (T*)”¹ jest macierzą odwrotną, a (x — A£*)^r “ wektorem transponowanym.

Wstawiając wzór (116) do (106), otrzymuje się bez trudu funkcję przynależności

Ć'(x) = -\(x-M:)^T(V)-'(z-M:) - i In [(2ir)"|Tⁱ|] + lnp‘. (119)

Łatwo pokazać, że funkcja (119) jest funkcją kwadratową ze względu na x,, przekształcając ją do postaci:

Ć'(x) = - iz^r(T-) ¹x + z'^r(T‘)"¹Mⁱ -    +

\ ¹ (120)

+ -ln [(2ir)ⁿ|T*|] + lnp*.

Jeśli jednak założy się (co zbyt często w praktyce przyjmuje się nieco bezkrytycznie!), że macierze kowariancji nie różnią się w sposób istotny(^u), to znaczy zakładając

(¹⁰) Dla poprawnego wyznaczenia elementów macierzy kowariancji konieczne jest dysponowanie dużą populacją (dużą liczbą obserwacji tworzących ciąg uczący N i każdy z podciągów N*).

(ⁿ ) Badanie zgodności wariancji przeprowadzić można za pomocą odpowiedniego testu statystycznego, będącego uogólnieniem na przypadek wielowymiarowy statystyki F Fishera.