img351

sq dodatnie: natomiast jeżeli macierz A jest dodatnio półokreślona, to wartości własne tego równania sq nicujcmne.

D4.13. Macierz symetryczna A nazywa się idempotentna gdy

A A = A² = A

Macierz idempotentna jest dodatnio półokreślona. Jest ona dodatnio określona wtedy i tylko wtedy, gdy jest macierzy jednostkowo. Macierz idempotentna ma wartości własne równe 1 lub 0. Stad też mamy równość:

tr(-4) = rz A

Forma kwadratowa, której macierz jest idempotentna. może być zredukowana do sumy kwadratów n zmiennych. Łatwo można sprawdzić, że macierz A z punktu D4.ll jest idempotentna oraz że można dokonać następującego przekształcenia:

n

Z (*_f-5)² = y?+.

i= I

Statystyczna niezależność nowych zmiennych losowych wynika z ortogonalności przekształcenia.

D4.14. Często wygodnie jest zapisywać macierze w postaci blokowej przez zestawienie dwóch lub większej liczby pewnych innych macierzy. Macierze blokowe maja na przykład postać:

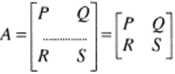
przy czym linie przerywane opuszcza się, gdy nie ma obawy o nieporozumienia. W powyższym wzorze macierze P i Q mają jednakowa liczbę wierszy, macierze P i R maja jednakowa liczbę kolumn, itd. Z definicji macierzy transponowanej wynika, że:

P^r	R^f
Q^r	~S^T

Iloczyn dwóch macierzy blokowych można otrzymać za pomocą reguł mnożenia traktując macierze jako elementy, np.:

351