img137

137

rytmicznę

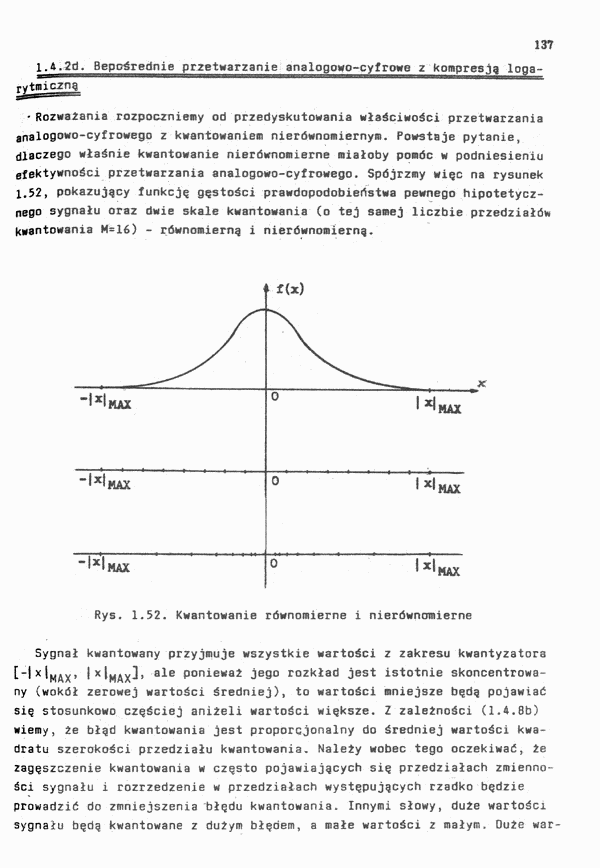
• Rozważania rozpoczniemy od przedyskutowania właściwości przetwarzania analogowo-cyfrowego z kwantowaniem nierównomiernym. Powstaje pytanie, dlaczego właśnie kwantowanie nierównomierne miałoby pomóc w podniesieniu efektywności przetwarzania analogowo-cyfrowego. Spójrzmy więc na rysunek 1.52, pokazujący funkcję gęstości prawdopodobieństwa pewnego hipotetycznego sygnału oraz dwie skale kwantowania (o tej samej liczbie przedziałów kwantowania M=16) - równomierną i nierównomierną.

	t(x)
"1*1 MAI	0	1 MAI
"1*1 «AX	0	1 ^X,MAX
“Nmax	ó	1 ^x'max

Rys. 1.52. Kwantowanie równomierne i nierównomierne

Sygnał kwantowany przyjmuje wszystkie wartości z zakresu kwantyzatora [-|x|_Max» ł^xlMAX^’ ^a*^e P°^nie*^aż jego rozkład jest istotnie skoncentrowany (wokół zerowej wartości średniej), to wartości mniejsze będą pojawiać się stosunkowo częściej aniżeli wartości większe. Z zależności (1.4.8b) wiemy, że błąd kwantowania jest proporcjonalny do średniej wartości kwadratu szerokości przedziału kwantowania. Należy wobec tego oczekiwać, że zagęszczenie kwantowania w często pojawiających się przedziałach zmienności sygnału i rozrzedzenie w przedziałach występujących rzadko będzie prowadzić do zmniejszenia błędu kwantowania. Innymi słowy, duże wartości sygnału będą kwantowane z dużym błędem, a małe wartości z małym. Ouże war-