img142

142

dv

H7

* k V

(1.4.20)

gdyż wtedy

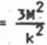
= const

(1.4.21)

Przebieg charakterystyki kompresji możemy wyznaczyć rozwiązując równanie różniczkowe (1.4.20) z warunkiem początkowy* y(1) = 1

y

£ lnv ♦ 1

(1.4.22)

v > 0

Na rysunku 1.54 przedstawiono^przebieg charakterystyki (1.4.22).

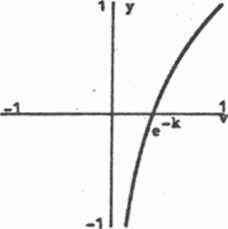
Rys. 1.54. Przebieg teoretycznej charakterystyki kompresji zapewniającej stałość odstępu sygnał - błąd kwantowania

Postaramy się teraz odpowiedzieć na pytanie, dlaczego właśnie logarytmiczna charakterystyka kompresji zapewnia niezależność odstępu sygnał -

-    błąd kwantowania od mocy sygnału. Stwierdzamy przede wszystkim, że małe wartości sygnału ulegają wzmocnieniu, i to tym silniejszemu, im poziom ich jest niższy. Sygnały mocne są z kolei tłumione. Mówimy, że układ o charakterystyce statycznej (1.4.22) realizuje kompresję sygnału (od tej chwili układy takie nazywać będziemy kompresorami), gdyż nie dość,.

że jego większe wartości chwilowe zostają stłumione, to jeszćze dodatkowo wartości mniejsze są wzmacniane. W efekcie końcowym otrzymujemy gęstsze kwantowanie sygnałów słabych i rzadsze silnych.

Zauważmy dalej, że logarytmiczna charakterystyka kompresji cechuje się tym, że względna szerokość przedziałów kwantowania (mierzona stosunkiem szerokości bezwzględnej q_A do odciętej V_A środka przedziału -

-    poziomu kwantowania) jest stała