img156

i zastępując odpowiednie sumy kwadratów lub iloczynów wyrażeniami:

U Y

im 1

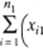
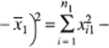
(8.37)

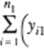
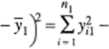
tyn

1=1

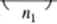
(8.38)

•I    -I

£(•*« “*1)^/1 -7i)= y»

±*n ty*

(8.39)

Podobnie należy postąpić z tymi fragmentami wzoru (8.33), które odnoszą się do grupy drugiej. Z powyższych wzorów, odpowiednio adaptowanych, należy również korzystać w dalszych obliczeniach.

Jeżeli nic ma podstaw do odrzucenia hipotezy o równoległości prostych regresji, wyznaczamy wartość b wspólnego współczynnika nachylenia obu prostych regresji w grupach jako:

«l    n₂

			l^+,?l
	/ij	2	^n2	2
	X ;=i		l^+£l
oszacowanie jego wariancji: V^2 rO- (h\ - ^A

"l    _ 2    "2    _;

l(^X“-^,X2

(8.40)

(8.41)

Granice ufności dla b można oszacować jako

(8.42)

156