img213

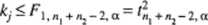
(11.30)

gdzie a oznacza przyjęty poziom istotności.

Przy takim postępowaniu rozważany obiekt może być zaliczony do jednej z dwóch danych zbiorowości, do obu zbiorowości albo wreszcie do żadnej z nich. Za pomocą relacji (11.30) otrzymujemy wokół każdego z obu środków v, i v₂ pewien obszar rozrzutu (rozproszenia), który z prawdopodobieństwem (1-a) zawiera w sobie obiekty rzeczywiście należące do rozpatrywanych klas.

Jeśli jednak chcemy w każdym przypadku podać jednoznaczne rozwiązanie problemu różnicowania, a więc jeśli szukamy najprawdopodobniejszej diagnozy, to trzeba się zdecydować na klasę o najmniejszej wartości kf.

gdy k_{ < k₂. wtedy klasa 1, gdy k_{ > k₂, wtedy klasa 2, gdy k_{ = k₂, wtedy klasa 1 lub klasa 2.

W przypadku, gdy pr/.y takiej dyskryminacji mają być uwzględnione tzw. prawdopodobieństwa aprioryczne /?, i p₂, gdy zatem zakłada się z góry, z jakim prawdopodobieństwem dany obiekt należy do klasy 1 lub do klasy 2, wówczas dobrze jest korzystać z wielkości

0=1.2)

(11.31)

Rozważany obiekt przydziela się do klasy z najmniejszą wartością /,. W przypadku p\ = p₂ ta reguła decyzyjna jest identyczna z uprzednią regułą.

Bardzo często pojawiającym się problemem jest możliwość zmniejszenia liczby rozpatrywanych cech pierwotnych⁶. Optimum jest bowiem uzyskanie przy możliwie najmniejszej liczbie cech możliwie największej miary dyskryminacyjnej.

W celu rozwiązania tego problemu określamy tzw. niezbędności poszczególnych cech )>•. Niezbędność U, cechy y, definiuje się jako wielkość, o jaką zmniejsza się miara dyskryminacyjna 7’², gdy ze zbioru wszystkich cech wyeliminuje się cechę yp

6 Proponujemy Czytelnikowi porównanie opisanego poniżej sposobu redukcji cech z metodami przedstawionymi w rozdziale dotyczącym regresji wielokrotnej. Wnioski mogą być pouczające!

(11.32)

213