img258

wprowadzenie odpowiednich mierników, określających globalna dokładność predykcji oraz szacujących istotność cząstkowych współczynników regresji.

Dokładność danego równania regresji wielokrotnej możemy określić za pomocą „odległości” między y, oraz y_h czyli za pomocą różnic (y, - y,-), a ściślej — kwadratów tych różnic.

Sumę

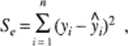
(12.8)

gdzie n oznacza liczebność próby, nazywa się suma kwadratów odchyleń od regresji lub resztowa suma kwadratów. Natomiast wielkość

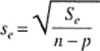
(12.9)

nazywa się błędem standardowym predykcji; jest ona miara dokładności przewidywania na podstawie równania

y = b₀ + b_]x_l+b₂x₂ + ... + b_px_p .

Im wartość s_e jest mniejsza, tym mniejsze różnice występują między przewidywanymi na podstawie równania regresji i obserwowanymi wartościami cechy Y. Można również wykazać, że j; jest estymatorem wariancji zmiennej losowej e, występującej w równaniu (12.1).

Określanie błędu standardowego predykcji na podstawie wartości S_e danej wzorem (12.8), jest o tyle niewygodne, że najpierw należy uzyskać oceny cząstkowych współczynników regresji b₀, b_{.....b_p, następnie wyliczyć z równania regresji wartości prze

widywane y, i dopiero wtedy zastosować wzór (12.8). Prościej jest obliczyć S_e ze wzoru:

n

(12.10)

S' = 2y}-R0_o,b b_p) ,

1=1

w którym pierwszy składnik oznacza sumę kwadratów obserwacji cechy Y (czyli zmiennej

zależnej), natomiast drugi składnik R (b₀. b_t.....b_p) to tzw. redukcja sumy kwadratów

w wyniku dopasowania wymienionych w nawiasach stałych.

Wiclkoć redukcji oblicza się ze wzoru:

(12.11)

K (V ^h\ v = b^Tw = b₀ly_i + />,    +... + b_p 'Lx_piy_i

258