lista 7

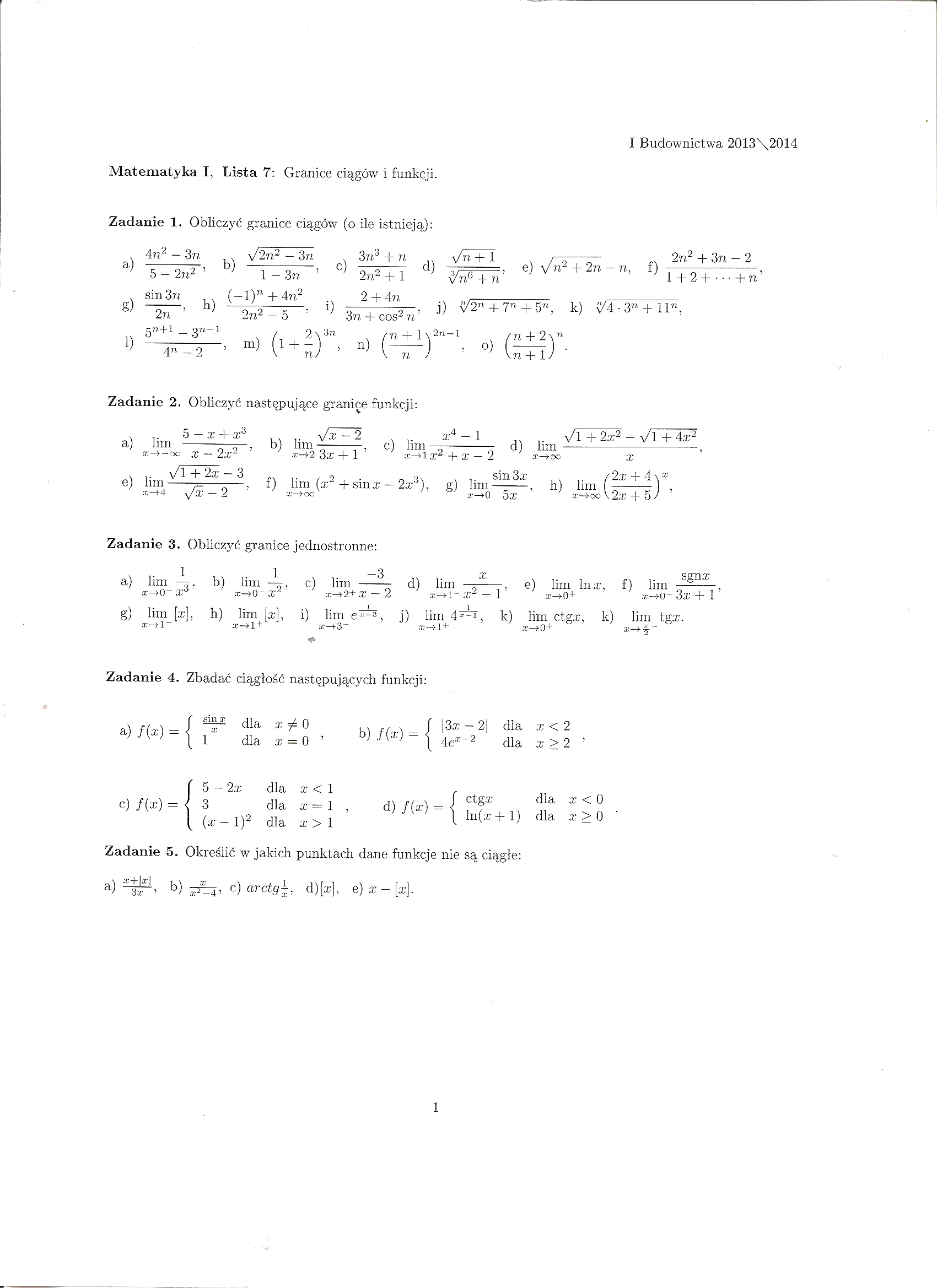
I Budownictwa 2013\2014

Matematyka I, Lista 7: Granice ciągów i funkcji.

Zadanie 1. Obliczyć granice ciągów (o ile istnieją): 4 n² — 3 n

a)

5 — 2n² ’

. . \J2 n² — 3 n . 3n³ + n

^b) —i-5-» ^c)

1 - 3n

g)

sin 3n

h)

2 n

5ⁿ⁺i — 3^n_1

(-l)ⁿ + 4 n 2n² - 5

2

2n² + ! 2 + 4 n

T ^d) y7⁺¹ » ^e) Vn² + 2n-n, f) 1 Vn^c> + n

2 n² + 3 n 1 + 2 + • • •

-2 + n

3n 4- cos² n

, j) 1/2” + 7ⁿ + 5". k) 1/4 ■ 3ⁿ + llⁿ,

n + 1 \ 2n—1

■ -> Kr ■>

o)

rt + 2 \ ⁿ

n + 1

Zadanie 2. Obliczyć następujące granice funkcji:

,    ..    5-x + x³

a)    hm -—2-,

®-»-oo rc - 2x²

d) lim

x-*oc

sin 3x

y/l + 2x² — y/l + 4x²

X

(2x+4\*

\/l + 2x - 3    . ..    . o .    ~ o. . .. smóx    /2x + 4\^rc

c)    lim--=—-—.    f) lun (x    + smx — 2ar), g) lun——,    h) lun --- ,

'    X—>4    y/x-2    ' x > X '    *->0 5x ' *-KJC V 2x    + 5 /

Zadanie 3. Obliczyć granice jednostronne:

d) lim —^^X    , e) lim Ina:, f) lim    ._;

3?—^ 1 “ 'JC    1    x—>-0"^    X—>0~ oX “f" 1

1    1    —3

a) lim —. b) lim —c) lim --

X^ó    x->0- X^z    x-J-2+ X — 2

g) lim [a;], h) lim [a;], i) lim e*-³, j) lim 4*-¹, k) lim ctga:, k) lim tgx.

x—>1^-    x-»l+    x—ł3~    ' x-»l ⁺    ’    x—>0⁺    x—

Zadanie 4. Zbadać ciągłość następujących funkcji:

a) f(x) =

K dla x 7 0 1    dla x — 0

i \ j. f \ i 13.7: — 21 dla x <2 ^b) /('' ) = •! Z-²    dla

(    5 -2x    dla    x    <    1

c) f(x) =    <    3    dla    x    =    1

I    (a; — l)²    dla    x    >    1

_rn _ 1 ^ctS* ^dla * < ⁰

_ln(_x+1) _{dla x}>₀ ■

Zadanie 5. Określić w jakich punktach dane funkcje nie są ciągłe: a) -^r±Lk, b)    c) arctg±, d)[x], e) x - [x\.

1