mech3a jpeg

364

1    9

kinetycznej równy jest — m v , gdyż energia kinetyczna w chwili początkowej jest równa zeru (^vo ⁼ 0)' Praca siły F będzie równa

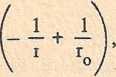
f - r^dr -

^ro ^r

stąd

1 ₂ / 1 1 \

~^mv =_qiq₂(^--_TJ.

Prędkość graniczna

r    ™ ^cm

= lim v = 20--

g^r    s

PRZYKŁAD 12.17 . Klocek o ciężarze P przymocowany jest do sprężyny o stałej c. Klocek utrzymywany jest na równi dodatkową siłą tak, że w chwili początkowej sprężyna jest nieodkształcona. Znając współczynnik tarcia /r i kąt a. znaleźć maksymalne przemieszczenie w dół po równi klocka, jeżeli zostaje on zwolniony bez prędkości początkowej (rys. 12.5).

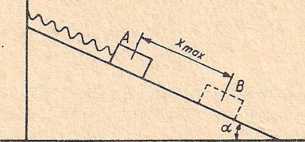
Rys 12.5

Rozwiązanie: Przyrost energii kinetycznej między położeniem A i położeniem B jest równy zeru (v_A = 0, v_fi = 0). Praca sił działających na klocek pomiędzy położeniem A i B jest równa

^{P sin} “ *max - ^{P 008} ° f“^xmax ~ J ^c *Lx ^{= E}B - ^EA = °-

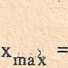
2 (P sin a — Pju cos a) c

stąd

PRZYKŁAD 12.18. Dwa nieważkie pręty OA = lj i OB = 1₂ (gdzie lj > 1₂) złączone są ze sobą na stałe pod kątem prostym. Na końcach prętów umieszczono kulki o ciężarach P| i P₂ (gdzie Pj > P₂).Znaleźć prędkość punktu B w chwili,gdy przechodzi on przez położenie poziome. Układ został puszczony z położenia I bez prędkości początkowej