Mechanika ogolna0022

44

kich punktów materialnych określonych względem bieguna O. Wielkość tę mo-

żerny zapisać inaczej w postaci wyznacznikowej:
n	i j k
o u M	^Xi Yj Zj
i=I	mj • x.j nij • y; m( • żi

Powyższy wyznacznik możemy przedstawić w postaci: K₀=K_xi + K_y-j + K_z-k

(93)

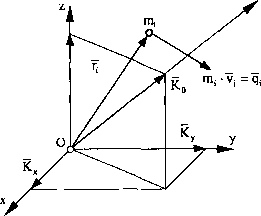
Wartość wektora krętu wyznaczymy z zależności:

K₀ = •y/K^ + K_y + K_z    (94)

Wielkości pod pierwiastkiem wyznaczamy, wykorzystując zapis wyznacznikowy, wówczas:

n

k_x =£^mi(yi’^żi^_zi‘y«)

i=l

n

^Ky ⁼⁼S^mi(^xi^-żi^_zi’ⁱi)

i=I

n

^Kz=Z^mi(^xi-yi-yi-^xi)

Podmie wzory (95) to rzuty wektora krętu określonego względem bieguna O na (lON/ezególne osie. Są to również wartości wektora krętu układu punktów mate-lirdnych, określonego względem odpowiednich osi. Równanie (93) możemy opisać w postaci:

K₀=K_X+K_y+K_z    (96)

gdzie: K_x - wektor krętu układu punktów materialnych określony względem osi x,

K_y - wektor krętu określony względem osi y,

K_z - wektor krętu określony względem osi z.

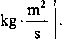
Inlnostką krętu w układzie SI jest

Itńwnanie (92) różniczkujemy względem czasu i otrzymujemy:

iś,=Ż(^^xmi •v_i)⁺Ż(^^xmi -^)-

i=l    i=l

Winny, że: rj = v_;, v_; = a_;, co uwzględnimy w podanym wzorze i otrzymamy: V( i, < m; • Vj hm x m; • Vj) = 0, ponieważ iloczyn wektorowy dwóch rów-

IM    i=l

nuleglych wektorów "wynosi 0 • W konsekwencji otrzymamy:

ⁿ . ,

^K o = Z ^{x m}i •'^)^:= Z ^{x m}i. ■') ■■

i=l

Ponieważ mj ■ aj =Pj +Fj, możemy więc zapisać:

^Ko    ^xmi ■5_i) = Z(i^:i xPi)+Z(^fi ^x^i)-

i=l    i=l    i=l

W lównaniu tym:

VM_n(I»_i) = X(^xP_i) to geometryczna suma wektorów momentów wszyst-

i-i    i-i

kii li sil zewnętrznych działających na układ punktów materialnych określonych względem bieguna O,