Mechanika ogolna0026

52
Wielkości te są zawsze dodatnie. W pewien sposób podają informację o rozmieszczeniu masy w układzie odniesienia. Można również określić masowy moment bezwładności względem bieguna, czyli:
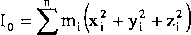
i=l
(108)
Moment bezwładności względem dowolnej osi lub bieguna możemy przedstawić w sposób umowny jako iloczyn masy całkowitej ciała i kwadratu pewnej odległości. Odległości te noszą nazwę promienia bezwładności ciała mierzonego względem danej osi lub bieguna. Wówczas masowe momenty bezwładności względem osi lub bieguna zapisujemy w postaci:
I* =m,ix
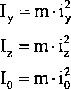
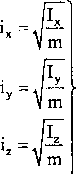
(109)
stąd:
(110)
Zależności (110) to tzw. promienie (ramiona) bezwładności, określające pewne odległości od osi lub bieguna całkowitej masy układu m.
('zęsto postępuje się w sposób odwrotny do opisanego, a mianowicie: poszukuje się masy, którą by trzeba skupić w pewnej odległości r od osi lub bieguna, aby olrzymać taki sam masowy moment bezwładności jak moment bezwładności badanego ciała. Masę taką nazywamy masą zredukowaną mzr ciała materialnego na daną odległość od osi lub bieguna. Tak np. masę zredukowaną na odległość r od osi x ciała materialnego, którego moment bezwładności względem osi x wynosi Ix, określono za pomocą równania:

Przykład 8
Mlueślimy masowy moment bezwładności jednorodnego cienkiego pręta względem osi symetrii z. Masa pręta wynosi m, a jego długość 1. Wymiary poprzeczne |ni;ln są bardzo małe w stosunku do jego długości, tak że możemy je pominąć.
|
Z 1 S |
k X c |
X X | |
Rys. 26 1/2 1/2
Wycinamy (w myślach) w odległości x od osi z element długości dx, co pokazami na rys. 26. Masa elementu długości dx wynosi dm = dx-p, gdzie p jest masą
właściwą pręta, czyli p = -y, zatem dm = ™dx .
Wńwczas masowy moment bezwładności pręta wynosi:
n 1/2 1/2 ,2
f dmi‘x.2= J px2-dx = y J x2 ‘dx =
1=1 (m) -1/2 1 -1/2 tZ
W tablicy 1 podano zależności określające masowe momenty bezwładności Względem odpowiednich osi wybranych ciał materialnych.
I alilli a I.
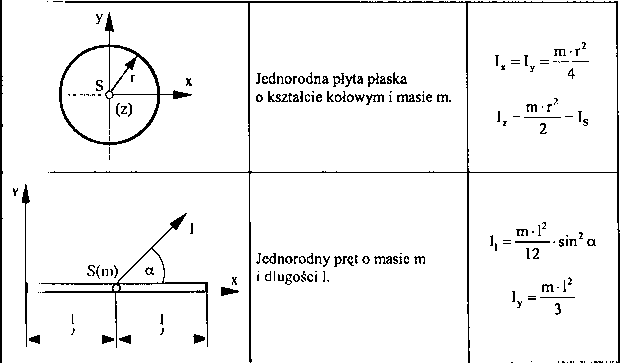
Wyszukiwarka
Podobne podstrony:
sposób. Wielkości te są podstawą do zaprojektowania filtru wejściowego. Jeżeli druga para biegunów b
Ronald Coase 1/2 Jak pisze M.BIaug." Niestety, koszty transakcyjne sa zawsze dodatnie, co spraw
89166 Mechanika Ogólna Wykład 2 pdf4 te o £mi6U9<e Pooód icto (aareundr!»C- ~ s°l ,7>6ir<
348 C. Goss, S. Kocańda w którym naprężenia i odkształcenia są zawsze dodatnie. Dla wyznaczenia stał
5 (1855) liczby sięgające nieco ponad 2 miliardy). Liczby te są pamiętane dokładnie. Drugi sposób re
Mechanika ogolna0022 44 kich punktów materialnych określonych względem bieguna O. Wielkość tę mo-
Mechanika ogolna0028 56 Są to wielkości skalarne, które mogą być (+), (-) lub równe zeru. Podają pew
Mechanika ogólna0028 56 Są to wielkości skalarne, które mogą być (+), (-) lub równe zeru. Podają pew
Mechanika ogólna0028 56 Są to wielkości skalarne, które mogą być (+), (-) lub równe zeru. Podają pew
Wielkości te nie są równoznaczne z wytrzymałością materiału. Istotnymi własnościami mechanicznymi
Mechanika ogolna0028 56 Są to wielkości skalarne, które mogą być (+), (-) lub równe zeru. Podają pew
więcej podobnych podstron