Mechanika ogolna0032

M

.5.2.2. Reakcje dynamiczne w łożyskach

Wyobraźmy sobie ciało sztywne osadzone na wale, który z kolei jest podparty w łożyskach A i B (rys. 33). Załóżmy, że środek masy nie leży w osi obrotu. Przyjmijmy układ odniesienia jak na rysunku. Położenie środka masy w układzie określimy, podając współrzędne: x_s, y_s, z_s.

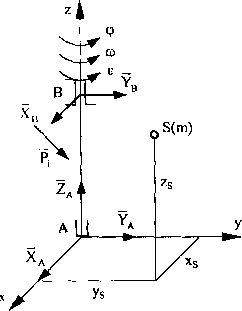
Równania dynamiczne opisujące ruch środka masy będą następujące: ^m-¹s=Z^Pix

i=l

n

(124)

m-y_s=X^Piy ■

i=l

n

i=l

Zgodnie ze wzorem (118) składowe przyspieszenia środka masy możemy zapisać:

Wprowadzimy wzory (125) do układu równań (124) oraz wykorzystamy równanie (121). Dostaniemy:

n

i=i	= -m-e-ys -m-co^2 -x
Ul	= m-e-xs - m-co^2 -ys
IX Ul	= 0
ŻMX Ul	(S)=-^i« -s+u-®^2
ŻMy	(Pi) = -Iy* -e-U

Ul

(126)

Układ (126) umożliwia określenie reakcji w łożyskach. Trzy pierwsze wzory wynikająz równań (124), a dwa następne z równań (121).

I Iw.iga!

Z równań (126) określamy reakcje w łożyskach. Zależą one od e i co

| co =    • Mówimy, że reakcje mają charakter dynamiczny, co ze wzglę

du na żywotność łożysk jest niekorzystne. Dlatego dążymy do takiego rozwiązania, aby bez względu na e i co reakcje miały charakter statyczny. Jeżeli środek masy leży na osi obrotu z, to:

x_s = Ol

k mówimy wówczas, że bryła jest wyważona statycznie.

y.s=oj

Jeżeli oś obrotu jest główną osią bezwładności, to: (idy spełnione są oba warunki, mówimy, że bryła jest wyważona dynamicznie, czyli wówczas oś zjest główną centralną osią bezwładności.

1

s =-e y_s-“^{Z 1}s y_s=e-x_s-0)²-y_s >