Mechanika ogolna0036

72

3.4. Dynamika układu brył

()pisując zjawisko ruchu układu brył, postępujemy wg następującej kolejności:

a)    na rysunku znaczymy wszystkie siły zewnętrzne działające na poszczególne bryły,

b)    w zależności od tego, jakim ruchem porusza się bryła, opisujemy ruch, podając różniczkowe równania ruchu,

c)    podajemy równania wynikające z zależności siłowych,

d)    określamy zależności kinematyczne układu.

Tak otrzymany układ równań rozwiązujemy.

1’rzykład 11

()pisać zjawisko ruchu mechanizmu płaskiego pokazanego na rys. 37.

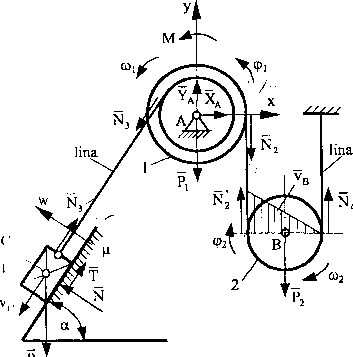
p - współczynnik tarcia, a - kąt pochylenia równi.

Nys. 37

Dane:

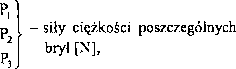
R, - promień dużego koła bryły 1 [m], r, - promień małego koła bryły 1 [m], r₂ - promień bryły 2 [m],

i® = i - promień bezwładności bryły

1 [m],

M = const. - moment siły działający na bryłę 1 [N-m],

Uównania opisujące ruch bryły 1:

(l)I^-(p₁=M + N₃-r₁-N₂-R₁,

(2) m, -x_A =0 = X_A -N₃ -cosa,

(3) m, • y_A 0-Y_a -N₃ -cosa-Nj -P,.

Pierwsze równanie opisuje ruch obrotowy bryły, dwa kolejne opisują ruch jej środka masy na kierunkach osi układu odniesienia. Środek masy się nie przemieszcza i z równań tych po znalezieniu sił napięcia lin (N₃, N₂) wyznaczymy trakcje w łożysku A.

Kównania opisujące ruch bryły 2:

(4) m₂ -x_B =0,

(5) m₂-y_B=N'₂+N₄-P₂, (ó)4²⁾-ćp₂=(N'-N₄)r₂.

I li yla 2 jest w ruchu płaskim. Równanie (5) opisuje ruch środka masy, równanie ((•) opisuje ruch obrotowy bryły względem środka masy.

Kównania opisujące ruch bryły 3:

(7)    m₃ • ii_c = P₃ ■ sin a - N₃ - T,

(8)    m₃ -w_c = 0 = N-P₃ cosa.

Iliyla 3 jest w ruchu postępowym. Przy opisywaniu ruchu postępowego bryły pn/,(islającej na równi korzystny jest taki dobór osi układu odniesienia (w tym przypadku u i w), aby jedna oś pokrywała się z kierunkiem równi, a druga była do niej prostopadła.

Po określeniu dynamicznych równań ruchu poszczególnych brył podajemy zależności siłowe układu. Zakładamy, że wszystkie liny w układzie są zawsze napięte. Będziemy więc mieli:

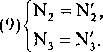
Następnie określamy zależności kinematyczne wynikające z rozkładu prędkości 1 hm nkturystycznych punktów układu, czyli:

fR, -co, = 2• v_B -2- r₂ -co₂,

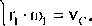
Wiadomo, że: