Mechanika ogolna0058

116
4.2.5. Moc układu
/miana pracy siły w odniesieniu do jednostki czasu nazywa się mocą chwilowi) siły, czyli:
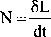
(179)
Na przykład w ruchu postępowym moc można określić następująco:
(180)
(181)
Nto=P.vs=Px-xs+Py.ys+Pz.żs
W przypadku ruchu obrotowego wokół osi z będziemy mieli:
N(o) =MZ - co
Jednostką mocy w układzie SI jest N • — = [ W].
4.2.6. Pole potencjalne sił
Załóżmy, że istnieje obszar (rys. 66) o tej właściwości, że na punkt materialny umieszczony w dowolnym punkcie obszaru działa siła zależna tylko od położę nia tego punktu. Każdemu punktowi obszaru odpowiada więc pewna niezmienna w czasie siła P, która działa na punkt materialny, gdy ten znajduje się w rozpatrywanym położeniu obszaru.
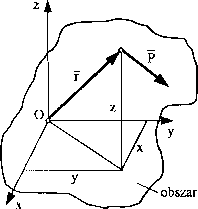
Rys. 66
Przestrzeń o takiej właściwości, że na dowolnie umieszczony w niej punkt małe lisi lny działa ściśle określona siła P, zależna tylko od położenia punktu, liazy winny polem sil:
P = P(r)
(182)
Jako przykład takiego pola można podać przestrzeń dokoła magnesu dla ciał ferromagnetycznych, pole grawitacyjne ziemskie, pole sprężyny itp. W mechanice interesuje nas przypadek pola grawitacyjnego sił. Określimy pracę wykonaną przez siłę P przy przejściu z położenia A do B (rys. 67).
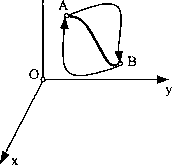
Rys. 67
J (Px-dx + Py-dy + Pz-dz).
(AB)
Praca całkowita wykonana przez siłę zależy od wielkości przebytej drogi. Jeżeli okaże się, że praca całkowita nie zależy od przebytej drogi, to takie pole sił nazywamy potencjalnym. Przez potencjał rozumiemy pewną skalarną funkcję położenia, czyli:
VA = V(x A, yA, zA) - tzw. potencjał w punkcie A,
VB = V(xB,yB,zB) - tzw. potencjał w punkcie B.
Pracę całkowitą wykonywaną przez siłę pola potencjonalnego określamy jako:

(183)
Jeżeli punkty A i B leżą na prostej równoległej do osi x układu odniesienia (rys. 68), to praca wykonywana przy przejściu z powierzchni A do B będzie równa:
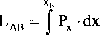
Wyszukiwarka
Podobne podstrony:
PA070087 [1600x1200] Moc - zdolność wykonywania pracy w określonym czasie (Energia / jednostka czasu
PA070087 [1600x1200] Moc - zdolność wykonywania pracy w określonym czasie (Energia / jednostka czasu
Mechanika ogolna0036 723.4. Dynamika układu brył ()pisując zjawisko ruchu układu brył, postępujemy w
Mechanika ogolna0052 Rys. 57 Wyrażenie i; x P; jest momentem siły Pj względem punktu O, co zapisze
Mechanika Ogólna Wykład 4 pdf4 OidadeczniC lolaifido łonu przeciw coc^ do orieo odnoóos^ % pf^dkob
pracy ( zadań, programu), do której realizacji zatrudnia się pracownika i której ukończenie powoduje
Nakład pracy studenta potrzebny do osiągnięcia efektów uczenia się ROK I II SEMESTR 1 1 2 3
Wskazówki do egzaminów Metaumiejętności Struktura procesu w koncepcji pracy z procesem (w odniesieni
więcej podobnych podstron