momenty3

S, =-2-19,2<12-3,93)=-309,9cm³,

= -2,52 cm.

S_y -309,9 A 123

Momenty bezwładności względem osi głównych centralnych:

J_yo= 2 [3600 + 42,3(2,52)² ]+ 2 [279 +19,2(9,48 - 3,93)² ] = 9480 cm⁴,    ,

J,₀ = 2 [248 + 42,3(8,5 - 2,23)² ]+ 2 ^9,6 +19,2(8,5+196)² ] = 8220 cm⁴.

Przykład 2.6    ]

Wyznaczyć położenie osi głównych centralnych i obliczyć momenty bezwłat ności względem tych osi dla przekroju z rys.2.6.

I 300

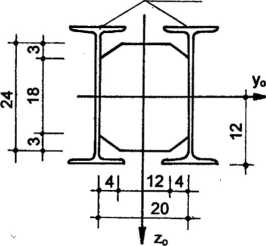
r 300    i

s = 125 mm, g= 10,8 mm A =69,1 cm²,

J_x = 9800 cm⁴, J_y = 451 cm*.

Rys.2.6

Przekrój ma dwie osie symetrii i one są osiami głównymi centralnymi. Momenty bezwładności względem nich są równe:

20-24³

^=2-9800+^—4

1,5-4-3^12-^

4-3³

36

+ 0,5-

24-20^3	_4[^3-^43
12	[ 36

= 39720 cm⁴,

J„=2[451 + 69,1(10 + 0,5-1,08)²]+^_T|5l-4|^- + 0,5-4-3fl0-|4

=30430cn

Wyznaczyć położenie osi głównych centralnych i obliczyć momenty bezwładności względem tych osi dla przekroju z rys. 2.7 złożonego z kształtowników walcowanych.

Rys. 2.7

Przyjmujemy dowolny układ osi współrzędnych (y,z). Najkorzystniej przyjąć go zgodnie z osiami głównymi centralnymi jednego z kształtowników. W naszym zadaniu zakładamy układ w środku ciężkości ceownika. Przez Ci, C₂, C₃ oznaczono środki ciężkości odpowiednio ceownika, dwuteownika i kątownika.

Wyznaczamy położenie środka ciężkości całego przekroju:

A =46,1 +48,3 + 19,2= 113,6 cm²,

S_z = £Ąy, = 46,1(- 12 - 2,36) + 19,2(-3,93-2,36) = -782,8 cm³,

S_y= £Ąz, = 46,1 (7,7) + 19,2 (-11,04) = 143,0 cm³,

-782,8

113,6

= - 6,89 cm,

143,0

113,6

1,26 cm.

19