Obraz0115

115

Podnosząc do kwadratu przekształconą zależność (6.12), otrzymujemy:

“ 2R_t' r₅ + ę ~^r! ~ ~

Pomijając wielkość Rj jako wartość niższego rzędu, otrzymujemy wzór na teoretyczną wysokość chropowatości w uproszczonej, często spotykanej, postaci:

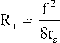
Przypadek, w którym chropowatość powierzchni obrobionej powstaje w wyniku odwzorowania na niej zaokrąglenia naroża i prostoliniowych odcinków krawędzi, przedstawia rys. 6.13b. Przypadek ten zachodzi, gdy:

. f    . f

K_r < arc sin —-, K_r < arc sin ■—

2r_s

a więc:

R_t = AD-sinK_r    (6.14)

ponieważ:

AD _ sin k;

BD sin^K_r + K;j

oraz

DB = f- ED - BC = f—r_e | tg-Ł +tg^

Zależność (6.14) można sprowadzić do postaci:

R_t =

sin K_r sin sin^K_r + k;]

f-r_£

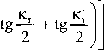
(6.15)

Z wyprowadzonych zależności wynika, że zmniejszenie chropowatości powierzchni obrobionej podczas toczenia można uzyskać, zmniejszając posuw