popr1piaps

Egzamin pisemny z PiAPS

1. Dany jest sygnał okresowy opisany wzorem: u (r) = sin⁴ (co₀1) + cos⁴ (co₀ r). Obliczyć napięcie skuteczne tego sygnału bez używania operacji całkowania.

Obliczyć wartość całki

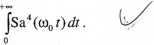
2.

3.    Określić warunki i podać przykład, kiedy widmo sygnału rzeczywistego jest

•    parzyste

•    urojone

•    dyskretne, ale nieokresowe

•    okresowe, ale ciągłe

•    równocześnie dyskretne i okresowe.

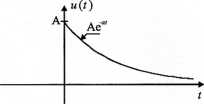
4.    Wyznaczyć i narysować funkcję autokorelacji r_uu(t) dla impulsu wykładniczego u(t) pokazanego na rysunku.

5.    Podać (bez dowodu) oba twierdzenia o splocie (pełny wzór!) dla transformacji Fouriera. 'V/'

6.    Posługując się wyłączenie definicją przekształcenia Fouriera oraz stosownymi twierdzeniami (bez dowodów), wyprowadzić wzór opisujący transformatę Fouriera sygnału okresowego o znanych współczynnikach F* rozwinięcia w zespolony wykładniczy szereg Fouriera.

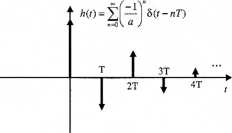
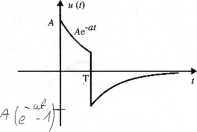
7. Na wejście układu o odpowiedzi impulsowej h{t) pokazanej na rysunku podano sygnał u(t) złożony z 2 impulsów wykładniczych. Wyznaczyć i narysować odpowiedź układu y(t).

8. Próbki pewnego sygnału przyjmują wartości /[n] = (-l)¹*. Jaki sygnał ciągły zostanie odtworzony w procesie idealnej rekonstrukcji? Wyprowadzić wzór i narysować ten sygnał.