s0048

Teoria Sygnałów - kolokwium

1. Obliczyć transformatę Fouriera impulsu parabolicznego pokazanego na wzorem:

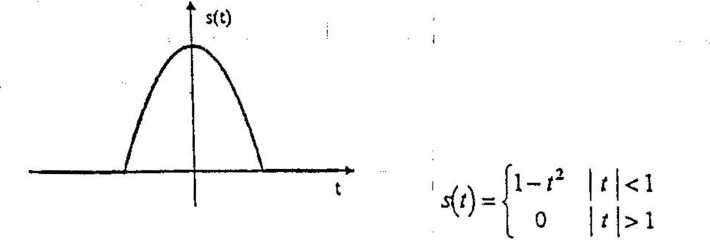
(1.5 pt)

rysunku i danego

2. Wyznaczyć odpowiedź na wymuszenie impulsem Diraca, a następnie wyznaczyć transmitancję i narysować charakterystykę amplitudową układu złożonego z sumatora oraz dwu elementów opóźniających:

y(t)

u(t) +i

—*3—*

-¹/,

(2 _Pt)

3. Obliczyć, jaka część energii sygnału j(/) = Sa^: (<d₀j) cos(2co₀/) zawarta jest w jego składowych widmowych o pulsacji 1 co | < 2co₀. (2 pt)

Teoria Sygnałów - kolokwium

1. Wyznaczyć transformatę Fouriera sygnału schodkowego według rysunku:    (1,5 pt)

*s(t)

A		A/2	AJ%
	T 2T 3T 4T... t

2. Sygnał został podany na wejście idealnego filtru gómoprzepustowego

o charakterystyce pokazanej na rysunku. Wyznaczyć postać czasowa^ sygnału obserwowanego na wyjściu filtru. (2 pt)

	j	H(jco)
		1
“^0		CO

sin^M ^w co₀r

3. Wykazać, że sygnał = — jest sygnałem o nieskończonej energii, (2 pt)