skanowanie0001

22. BADANIE ATOMOWYCH WIDM EMISYJNYCH

GAZÓW I METALI

Atom wodoropodobny

Atomem wodoropodobnym nazywamy atom złożony z jądra obdarzonego dodatnim ładunkiem Ze (gdzie Z jest liczbą naturalną, a e oznacza wartość ładunku elementarnego) oraz krążącego wokół niego elektronu. Zgodnie z teorią Bohra elektron w atomie może poruszać się tylko po ściśle/ określonych orbitach stacjonarnych, dla których spełniony je^t warunek:

L = m v r = n    ,    (22.1®

gdzie . L oznacza moment^^pędu,. elektronu krążącego po danej orbicie, m jego masę, v - prędkość liniową elektronu w ruchu po orbicie, r - promień orbity⁵, h - stałą Plancka^ n - tzw. główną liczbę kwantową określającą orbitę, na której znajduje się elektron (n może przyjmować wartości całkowite, dodatnie

9 ²—^^B .i,li B    B

Energia elektronu w atomie może przyjmować tylko ściśle określone, dyskretne wartości    E^, - E₂,..., E_r odpowiadające

kolejnym wartościom głównej liczby kwantowej n, a więc kolejnym orbitom elektronowym.

Wartość energii E_R stanu elektronowego opisanego główną liczbą kwantową n można łatwo obliczyć korzystając z równania (22.1) oraz z faktu, iż w przypadku orbity stacjonarnej.

• i• dośrodkowy działającą na elektron jest siła oddziaływania hyiombOWBkiego pomiędzy jądrem atomowym a elektronem. Wartość ■iim• i ij I i E opisuje następujący wzór:

(22.2)

E = - ^7,2 e4 m

ⁿ '    8c²h²n²

o

-i*l.-.ii) c_q oznacza przenikalność elektryczną próżni.

Krążąc po danej orbicie stacjonarnej elektron nie zmienia iwoJoj energii.

_s Emisja promieniowania elektromagnetycznego występuje tylko i * i my przejściu elektronu ze stanu stacjonarnego o większej minr^ii Ej do innego stanu stacjonarnego o mniejszej energii M,. Podczas takiego przejścia emitowany jest kwant energii |ii'H (foton) o częstotliwości y j^ określonej wzorem:

v

ji

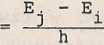
(22.3)

na

w wyniku

Przejście elektronu z orbity o mniejszej energii Orbitę o większej energii Ej jest możliwe jedynie nlisorpcji fotonu o energii równej różnicy energii Ej

Widmo promieniowania atomu wodoropodobnego

Korzystając z (22.2) oraz (22.3) możemy znaleźć wzór określający częstotliwość promieniowania emitowanego lub absorbowanego przez atom wodoropodobny przy przejściu ze stanu opisanego główną liczbą kwantową nj do stanu opisanego liczbą

ⁿi    ^? ■■ i i

cR Z" oo

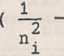
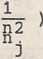
(22.4)

gdzie c oznacza prędkość propagacji światła w próżni, natomiast