skanowanie0065 (2)

Moment bezwładności układu zredukowany do osi O

kg-m²

71    ,

, = — mr"

Przykład 6.17. Na rysunku 6.17 przedstawiono układ trzech kół i dwa ciężary

0    masach m kg. Koło ruchome o masie m kg i promieniu r m toczy się bez poślizgu po poziomym torze. Współczynnik tarcia tocznego jest równy f Jeden z ciężarów leży na chropowatej równi pochyłej o kącie pochylenia a, a współczynnik tarcia ślizgowego wynosi fi. Stały moment M N • m jest przyłożony do koła o masie 2 m

1    promieniu 2r, obracającego się względem osi 0. Z kołem tym połączono

i i •

A

lii Vt

Ml	li)
i	tlili (

kątowe 8_t i e₂ oraz przyspieszenia liniowe a_lt a'₂ i a₃. Ponadto wyznaczyć moment bezwładności układu zredukowany do osi O. W chwili początkowej układ znajdował się w spoczynku.

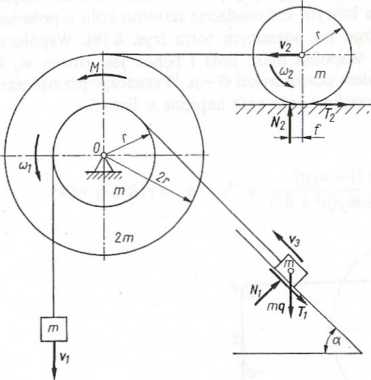
Rys. 6.17. Do przykładu 6.17

Rozwiązanie. Energia kinetyczna końcowa wynosi

E.2 = T^myi+T

mr² 2m(2r ~2~2~

,1    , 1 mr jfij 1    ,•

(oi+-mvi+—-j- coi^nwi

Praca sił ciężkości i tarcia oraz momentów M i Nf jest równa

Po uwzględnieniu zależności między prędkościami liniowymi i kątowymi, drogami i kątami obrotu oraz wartościami siły normalnej N₂ i tarcia T_y

v, = co_l r,    (o_x -2r = co₂r,    v₂ = co₂r,    v₃ = co₁r

s_l=<p₁r,    <p₁-2r = (p₂r,    s₂ = (p₂r,    *_s. ffit-

N₂ = mg,    T_x = fimg cosa

otrzymamy

/

+ m <7 r sin a—fimgrcosoć)

Stąd

d>f(ll,5mr²) = <p_x [m^r(l+śina—/icosa)+M—2mgf]

Po zróżniczkowaniu obu stron tego równania względem czasu otrzymamy

1

2

•2o)₁

d ojj dt

(ll,5mr²)

dtp i dt

[mgr(l +sina—jueosa)+M—2mgf~\

Zatem

M_zred0 mgr{\ +sina—jUCOsa)+M—2mgf ⁶l_XI7⁼    ll,5mr²

Pozostałe przyspieszenia kątowe i liniowe wynoszą e₂ = 2e_x, a_x = e^,    a₂ = 2e_tr,    a₃=e_xr

Moment bezwładności układu zredukowany do osi 0 wynosi Izredo = n,5mr²

Przykład 6.18. Na rysunku 6.18 pokazano układu pięciu kół i jedno ciało o masie m kg leżące na chropowatej równi pochyłej o kącie pochylenia /? i współczynniku tarcia ślizgowego g.. Koło ruchome o masie m i promieniu r toczy się bez poślizgu po równi pochyłej o kącie pochylenia a. Współczynnik tarcia tocznego wynosi f Stały moment M N • m jest przyłożony do koła o masie