skanuj0090

180

Krzywa zależności prądu anodowego od potencjału anody V_a, mierzonego względemi katody (tzw. charakterystyka prądowo-napięciowa) przedstawiona jest na rys.2.

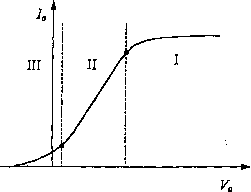
Rys.2. Charakterystyka prądowo-napięciowa

Przy dodatnim potencjale V_a pole elektryczne E wytworzone między anodą i katodą przyspiesza elektrony w kierunku anody. Dla dostatecznie dużych potencjałów V_a wszystkie wyemitowane przez katodę elektrony dochodzą do anody, a prąd anodowy /„ prawie nie zależy od potencjału anody i przyjmuje maksymalną wartość prądu nasycenia l_n (obszar prądu nasycenia - obszar I na rys.2). Elektrony poruszające się w bańce wytwarzają dodatkowe pole elektryczne E’, które nakłada się na pole E wytworzone przez zewnętrzną różnicę potencjałów. W obszarze prądu nasycenia wypadkowe pole E + E’ działa przyspieszająco na elektrony w całej objętości bańki. Zmniejszenie V_a powoduje również zmniejszenie pola E tak, że poniżej pewnej wartości V₀ wypadkowe pole przy katodzie będzie działało na elektrony hamująco. Wtedy prąd anodowy 7_a maleje wraz ze zmniejszaniem się potencjału anody (obszar ładunku przestrzennego - obszar II na rys.2). Zależność tę opisuje prawo Langmuira:

L=DV„

gdzie: D - stała charakterystyczna dla danej bańki próżniowej.

Dalsze zmniejszanie potencjału V_a powoduje, że wypadkowe pole: E + E’ działa na elektrony hamująco w całej objętości bańki, a do anody docierają tylko nieliczne elektrony, które w momencie emisji uzyskały duże prędkości początkowe. Ta część charakterystyki prądowo-napięciowej nazywa się zakresem prądu początkowego (obszar III na rys.2). Zależność prądu anodowego od potencjału anody w tym obszarze opisuje zależność:

eV„

I_a=h*^kT,

gdzie /o charakteryzuje daną bańkę próżniową.

Z katody mogą się wydostać tylko te elektrony, których energia kinetyczna odpowiadająca składowej prędkości prostopadłej do powierzchni metalu jest co najmniej równa pracy wyjścia W. Zgodnie z rozkładem Fermiego-Dirąca prawdopodobieństwo tego, że elektron w metalu ma energię E dane jest wzorem:

P{E) =

C

E-E_f

e ^kT +1 gdzie: C - stałą ~ energia Fermiego.

W niskich temperaturach prawdopodobieństwo tego, że elektron ma energię równą pracy wyjścia W jest niewielkie. Wraz ze wzrostem temperatury rośnie liczba elektronów posiadających energie kinetyczne większe od pracy wyjścia. Zależność gęstości prądu termoemisji od temperatury podaje prawo Richardsona-Dushmana:

(1)

j = AT¹ e~^ir

gdzie: W- praca wyjścia, A - stała.