skanuj0154

Ćwiczenie 28 *

Siatka dyfrakcyj na

I. Wprowadzenie

I Iwaga: Obowiązuje teoria dyfrakcji i interferencji światła zawarta w ćwiczeniu 27.

Siatka dyfrakcyjna to układ N wzajemnie równoległych i rozmieszczonych w równych odstępach szczelin. Odległość d środków sąsiednich szcże-lin nazywamy stałą siatki. Dyfrakcja światła na układzie N szczelin jest rozszerzeniem interferencyjno-dyfrakcyjnego eksperymentu z dwoma szczelinami (ćw.27). Jeżeli na siatkę pada równoległa wiązka światła monochromatycznego o długości A, to każda szczelina będzie źródłem pęku promieni ugiętych pod różnymi kątami. Otrzymany rozkład natężenia światła na ekranie jest podobny do obrazu otrzymanego w przypadku dwóch szczelin i składa się z serii prążków interferencyjnych, których względne natężenie modulowane jest przez obraz dyfrakcyjny pojedynczej szczeliny.

Promienie, wychodzące ze wszystkich szczelin i tworzące z pierwotnym kierunkiem kąt a, będą się wzajemnie wzmacniały, gdy różnica dróg Smiędzy dwoma sąsiednimi ugiętymi promieniami równa jest wielokrotności długości fali (rys.l):

5- dsma_n - nA, n = 0,1,2, 3,...    (1)

Równanie (1) określa położenie maksimów głównych natężenia światła.

(iznacza to, że odległość kątowa prążków jest określona stosunkiem AJd i nie zależy od liczby szczelin N. Dla n = 0 otrzymujemy prążek zerowy odpowiadający wiązce nieugiętej, dla n = 1, 2,..., k otrzymujemy prążki ugięte pierwszego, drugiego, k - tego rzędu. Jeżeli padające światło jest mieszaniną fal o różnych długościach, to położenia maksimów natężenia odpowiadają różnym kątom a„. Każdy rząd rozciąga się w widmo pierwsze-’ Opracowała M.Duraj.

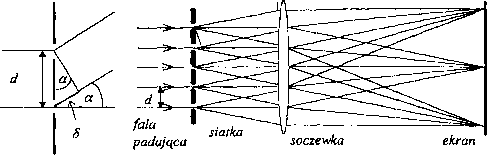
Rys.l. Ugięcie światła na siatce dyfrakcyjnej, d — stała siatki. Soczewka skupia w punkcie P promienie równoległe po przejściu przez szczeliny siatki. Różnica dróg optycznych: 5 = dsina, a- kąt ugięcia

go, drugiego, «-tego rzędu. Liczba otrzymywanych rzędów jest ograniczona stałą siatki d, zgodnie z warunkiem: n/L/d <1.

Równanie (1) jest analogiczne do równania określającego położenia maksimów natężenia światła otrzymanego w wyniku interferencji na dwóch szczelinach. Ze wzrostem liczby szczelin N maleje szerokość maksimów głównych, pomiędzy nimi pojawia się N-1 minimów bocznych oraz N-2 maksimów wtórnych o bardzo małym natężeniu, wywołanych wzmacnianiem się promieni pochodzących z mniejszej liczby szczelin. Położenie kątowe fc-tego minimum, leżącego pomiędzy kolejnymi maksimami głównymi określa równanie:

sinOk = M/Nd, Jfc= 1, 2,..JV-1    (2)

Dla k = N otrzymujemy już maksimum główne. Gdy rośnie liczba szczelin, w tym samym stosunku rośnie liczba minimów i maksimów wtórnych (rys.6). Szczegółowa analiza obrazu powstającego na ekranie w zależności od liczby szczelin siatki została przedstawiona w Uzupełnieniu.

Dyspersja kątowa siatki jest miarą odległości kątowej dwu linii utworzonych przez dwie monochromatyczne fale, których długości różnią się od siebie o AA (SA). Aby otrzymać dyspersję kątową różniczkujemy wyrażenie (1):

D =

da

SA

n

c/cosa

(4)