Skan"

Richtungskosinus einer Geraden und ihre Parameterdarstellung in der Ebene und im Raum.

Definition 1. Der Winkel xOA zwischen der positive Ox-Achse eines rechtwinkligen Koordinatensystem ais erstem Schenkel und dem Halbstrahl OA (Fig.l.) heiBt erster Richtungswinkel mit der MaBzahl ę<2 n.

Definition 2. Der Winkel AOy zwischen dem Halbstrahl OA ais erstem Schenkel und der positiven Ordinatenachse Oy ais zweitem Schenkel heiBt zweiter Richtungswinkel mit der MaBzahl /?(|/?| < 2n).

A

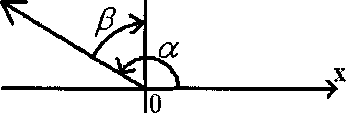
Fig.l. Richtungswinkel in der Ebene

Definition 3. Die Richtungswinkel eines beliebigen Strahls in einer Ebene, (der nicht durch den Anfang des Koordinatensystem zu gehen braucht), in Bezug auf dieses System sind die Richtwinkel eines parallelen und durch den Anfang gehenden Strahles.

Definition 4. Die Kosinus der Richtungswinkel (Definition 1 und 2) heiBen beziehentlich erster und zweiter Richtungskosinus. Bezeichnet man die Richtungskosinus beziehentlich mit

v_x =cos a

(1)

(2)

v_y = cos fi

und beriicksichtigt den aus Fig.l. abzulesenden Zusammenhang

/j 7t    71

ot + u = — <=> B ---a

2    2

dann gilt

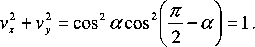
(3)

Denkt man sich auf dem Strahl g (Fig.2.) einen Einheitsvektor v d.h. einen Yektor mit der Lange 1 und der