str11 (3)

(14.219)

nazywamy równaniem charakterystycznym macierzy A.

Pierwiastki tego równania A,j, A,₂,..., X.„ nazywamy pierwiastkami charakterystycznymi lub wartościami własnymi macierzy kwadratowej A. Każdy wektor niezerowy x_: spełniający równanie

Ax- =

(14.220)

nazywamy wektorem własnym macierzy A odpowiadającym A*

Jeżeli macierz A ma różne wartości własne, tzn. nie analizujemy przypadku pierwiastków wielokrotnych, to każdej wartości własnej odpowiada jeden liniowo niezależny wektor własny, czyli

Ax,

Ax₂

Ax.

—

= A₂^X2

= K*,.

(14.221)

Twierdzenie Cayleya-Hamiltona

Zgodnie z twierdzeniem Cayleya-Hamiltona każda macierz kwadratowa spełnia swoje równanie charakterystyczne. Jeżeli więc równanie charakterystyczne macierzy A ma postać

to jest spełnione równanie

g(A) = 0

(14.222)

0(A) = 0

(14.223)

Przykiad 14.7

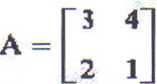
Wyznaczymy    wartości własne i określimy wektory własne macierzy kwadratowej

Wartości własne macierzy A otrzymamy jako pierwiastki równania

1-3

-2

-4

1-1

= l²—41-5

0

Stąd

- 5;    1₂ = - l

Oznaczymy dwa wektory własne

11